Что такое сложение в математике

Сложение в математике – это операция, которая позволяет суммировать два или более числа и находить их общую сумму. Узнайте, как правильно складывать числа и научитесь решать простые математические задачи по сложению.

Сложение — одна из основных операций в математике, позволяющая объединить два или более числа в одно число, называемое суммой. Эта операция широко применяется в повседневной жизни и используется для решения различных задач. Понимание и умение сложить числа являются неотъемлемыми навыками в обучении математике.

Правила сложения достаточно просты. Для сложения двух чисел их нужно поставить одно под другим таким образом, чтобы единицы, десятки, сотни и т.д. находились в одном столбце. Затем сложите числа в каждом столбце, начиная справа, и запишите результат под строчкой. Если сумма чисел в столбце превышает 9, необходимо добавить единицу к следующему столбцу. Продолжайте сложение до тех пор, пока числа не закончатся.

Например, для сложения чисел 56 и 23 вам нужно поставить 56 под 23 и начать сложение справа: 6 + 3 = 9, затем 5 + 2 = 7. Таким образом, сумма чисел 56 и 23 равна 79.

Сложение можно применять не только к целым числам, но и к десятичным и дробным числам. При сложении десятичных чисел нужно обратить внимание на позицию десятичной запятой и сложить числа в каждом столбце, начиная справа от запятой. При сложении дробей нужно привести их к общему знаменателю и сложить числители.

Сложение является одной из фундаментальных операций в математике, и хорошее понимание правил и навыков сложения является основой для изучения более сложных математических концепций.

Определение сложения в математике

Сложение выполняется с помощью слагаемых и суммы. Слагаемые — это числа, которые складываются. Сумма — результат сложения.

Правила сложения включают:

1. Сложение можно выполнять с любыми числами — натуральными, целыми, рациональными или действительными.
2. Порядок слагаемых не влияет на сумму, то есть a + b = b + a.
3. Сложение ассоциативно, то есть (a + b) + c = a + (b + c).
4. Ноль является нейтральным элементом сложения, то есть a + 0 = a.
5. Сложение числа a с противоположным числом -a дает ноль, то есть a + (-a) = 0.

Примеры сложения:

• 2 + 3 = 5
• 7 + (-4) = 3
• 0 + 9 = 9
• 4 + 6 + 2 = 12

Сложение является одной из базовых операций в математике и имеет широкое применение в повседневной жизни, науке и других областях.

Что такое сложение?

В сложении участвуют два числа – слагаемые. Результат сложения называется суммой. Сложение обозначается знаком «+». Например, 2 + 3 = 5.

Правила сложения просты:

1. Сложение коммутативно: порядок слагаемых не важен. Например, 2 + 3 = 3 + 2.
2. Сложение ассоциативно: можно складывать числа в любом порядке. Например, (2 + 3) + 4 = 2 + (3 + 4).
3. Сложение нулевого элемента: к любому числу можно прибавить ноль, и результат останется неизменным. Например, 5 + 0 = 5.

Сложение широко используется для решения различных задач и в повседневной жизни. Например, при покупке товаров, оплате счетов или подсчете времени.

В математике существуют также различные методы и стратегии для выполнения сложения, такие как столбиковое сложение или сложение в уме.

Понимание и умение выполнять сложение является важным навыком для дальнейшего изучения математики и решения различных задач.

Правила сложения

Правило 1: Порядок слагаемых не влияет на сумму. То есть, можно менять местами числа, которые складываются, и результат останется тем же.

Правило 2: Сложение чисел можно выполнять по частям. Например, для сложения числа 4 с числом 5 можно сначала сложить 4 + 1, а затем добавить к результату еще 4.

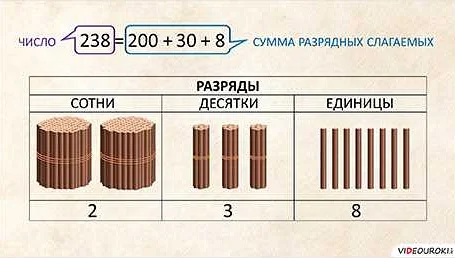
Правило 3: Для удобства сложение часто представляют в виде вертикальных столбиков. При этом разряды чисел выравниваются, а сложение производится по разрядам, начиная справа. Если сумма разряда больше 9, то переносится единица в следующий разряд.

Пример:

23
+ 15
——
38

В этом примере мы сначала сложили 3 + 5, что дает 8, а затем сложили 2 + 1, получив 3. Итоговая сумма составляет 38.

Правило сложения чисел

Правило сложения чисел гласит, что для сложения чисел нужно складывать их цифры по порядку, начиная с самого младшего разряда.

Например, для сложения чисел 123 и 456, мы начинаем с суммирования цифр единиц (3+6=9), затем цифр десятков (2+5=7), и наконец цифр сотен (1+4=5). Итого, получаем сумму 579.

Если при сложении получается сумма больше 9, то в результирующей сумме записывается только последняя цифра, а остаток переносится на следующий разряд.

Например, при сложении чисел 789 и 456, сначала мы складываем цифры единиц: 9+6=15. В результате, записываем 5 и переносим 1 на разряд десятков. Затем складываем цифры десятков: 8+5+1=14. Записываем 4 и переносим 1 на разряд сотен. Наконец, складываем цифры сотен: 7+4+1=12. В результате, записываем 2 и переносим 1 на разряд тысяч. Окончательно, получаем сумму 1245.

Таким образом, правило сложения чисел помогает нам правильно складывать числа и получать их сумму.

Правило сложения дробей

Для сложения дробей необходимо иметь дроби с одинаковым знаменателем. Если знаменатели дробей различаются, то их необходимо привести к общему знаменателю.

Правило сложения дробей выглядит следующим образом:

Для сложения дробей с одинаковыми знаменателями складываем числители и записываем полученную сумму над общим знаменателем.

Например, для сложения дробей 2/3 и 1/3, мы складываем числители и записываем полученную сумму над общим знаменателем 3: 2/3 + 1/3 = 3/3 = 1.

Если знаменатели дробей различаются, приводим их к общему знаменателю путем нахождения их НОК (наименьшего общего кратного). Затем, умножаем каждую дробь на такое число, чтобы ее знаменатель стал равным общему знаменателю. После этого, сложение дробей происходит по правилу для дробей с одинаковыми знаменателями.

Например, для сложения дробей 1/2 и 3/4, найдем их НОК, который равен 4. Затем, умножим первую дробь на 2/2 и вторую дробь на 4/4, чтобы получить дроби с общим знаменателем 4: 1/2 * 2/2 = 2/4 и 3/4 * 4/4 = 12/16. И наконец, сложим полученные дроби: 2/4 + 12/16 = 14/16 = 7/8.

Правило сложения отрицательных чисел

При сложении отрицательных чисел в математике применяются следующие правила:

1. Если перед отрицательным числом нет знака операции, то считается, что перед ним стоит знак «плюс». Например, сложение (-5) и (-3) будет выглядеть так: -5 + (-3).
2. При сложении двух отрицательных чисел, их абсолютные значения складываются, а знак минус сохраняется. Например, (-5) + (-3) = -8.
3. Если перед отрицательным числом стоит знак операции «плюс», то сложение осуществляется по правилам сложения положительных чисел. Например, (+5) + (-3) = 2.

Таким образом, правило сложения отрицательных чисел сводится к сложению их абсолютных значений с сохранением или изменением знака.

Примеры сложения

Пример 1: 2 + 3 = 5

В данном примере мы складываем числа 2 и 3. Сумма этих чисел равна 5.

Пример 2: 7 + 9 = 16

В этом примере мы складываем числа 7 и 9. Их сумма равна 16.

Пример 3: 12 + 8 = 20

В данном примере мы складываем числа 12 и 8. Их сумма равна 20.

Пример 4: 25 + 15 = 40

В этом примере мы складываем числа 25 и 15. Их сумма равна 40.

Пример 5: 50 + 50 = 100

В данном примере мы складываем числа 50 и 50. Сумма этих чисел равна 100.

Таким образом, сложение позволяет объединять числа и находить их сумму.

Пример сложения двух чисел

Чтобы проиллюстрировать процесс сложения в математике, рассмотрим пример с двумя числами: 5 и 3.

Шаг 1: Начнем с первого числа, 5. Затем прибавим к нему второе число, 3.

Шаг 2: Сложим 5 и 3. Получим сумму 8.

Итак, результат сложения чисел 5 и 3 равен 8.

Пример сложения дробей с общим знаменателем

Рассмотрим пример сложения дробей:

• Дано: $\frac{1}{4} + \frac{3}{4}$
• Знаменатель у обеих дробей равен 4, значит, они имеют общий знаменатель.
• Сложим числители: $1 + 3 = 4$.

Таким образом, $\frac{1}{4} + \frac{3}{4} = \frac{4}{4}$.

Дробь $\frac{4}{4}$ является равной единице, поэтому окончательный результат сложения будет равен 1.

Таким образом, при сложении дробей с общим знаменателем, достаточно сложить числители и записать результат с общим знаменателем.

Пример сложения чисел с противоположными знаками

Например, если нужно сложить числа -7 и 3, то сначала находим их абсолютные значения, которые будут равны 7 и 3 соответственно. Затем определяем число с большим по модулю значением, в данном случае это число -7. Так как -7 имеет отрицательный знак, то и результат сложения будет иметь отрицательный знак. Окончательно, результат сложения чисел -7 и 3 будет равен -4.

Видео по теме:

Как определить сложение в математике?

Сложение в математике — это операция, позволяющая объединять два числа в одно, называемое суммой. Оно выполняется путем сложения чисел друг с другом, при этом результатом является число, равное сумме слагаемых.

Каким образом сложение применяется в повседневной жизни?

Сложение применяется в повседневной жизни постоянно. Например, при покупке продуктов в магазине нужно сложить цены разных товаров, чтобы узнать общую сумму. Также сложение используется при расчете времени, при подсчете денег, при планировании бюджета и многих других ситуациях.

Что произойдет, если сложить число с нулем?

Если сложить число с нулем, то результатом будет само это число. Например, 5 + 0 = 5. Ноль является нейтральным элементом для сложения, поэтому при сложении любого числа с нулем, число не изменится.