Что такое сложное выражение в математике 3

Сложное выражение в математике 3 объединяет различные операции и элементы, такие как скобки, степени, корни, логарифмы и тригонометрические функции. Понимание и умение разбираться с такими выражениями является важным навыком для решения сложных математических задач и применения их в реальной жизни.

Сложное выражение – это математическое выражение, которое содержит несколько операций и переменных. Оно может быть использовано для решения сложных задач и вычислений. Для работы с такими выражениями необходимо знать основные понятия и правила.

Одно из основных понятий – это операции. В математике используются различные операции, такие как сложение, вычитание, умножение и деление. Кроме того, существуют операции возведения в степень и извлечения корня. В сложных выражениях эти операции могут быть комбинированы для получения нужного результата.

Например, выражение 5 + 2 * 3 является сложным, так как содержит две операции – сложение и умножение. В этом случае, умножение будет выполнено первым, затем сложение.

Другим важным понятием является переменная. Переменная – это символ, который представляет неизвестное значение или элемент множества значений. Она может принимать различные значения и использоваться в выражениях для получения разных результатов.

Например, в выражении 2 * x + 3, переменная x может принимать разные значения, что позволяет получить различные результаты. Значение x может быть задано явно или определено в ходе решения задачи.

Сложное выражение в математике 3: основные понятия и примеры

Сложное выражение в математике представляет собой математическую конструкцию, состоящую из нескольких операций и операндов. Оно может содержать различные арифметические операции, скобки, степени, корни и другие математические символы.

Основными понятиями, связанными со сложными выражениями, являются операции и операнды. Операции — это действия, которые выполняются над операндами, такие как сложение, вычитание, умножение и деление. Операнды — это числа или переменные, над которыми выполняются операции.

Примеры сложных выражений:

• 3 + 4 * 2 — в данном выражении сначала выполняется умножение, а затем сложение. Результатом будет 11.
• (5 — 2) * (8 + 1) — здесь сначала выполняются операции в скобках, а затем умножение. Результатом будет 27.
• 23 — 1 — данное выражение содержит степень. Результатом будет 7.
• sqrt(9) + 2 — в этом примере используется функция корня. Результатом будет 5.

Сложные выражения позволяют выполнять различные математические вычисления. Они являются важным инструментом в математике и используются как в ежедневной жизни, так и в специализированных областях, таких как физика, экономика, программирование и другие.

Сложное выражение: определение и свойства

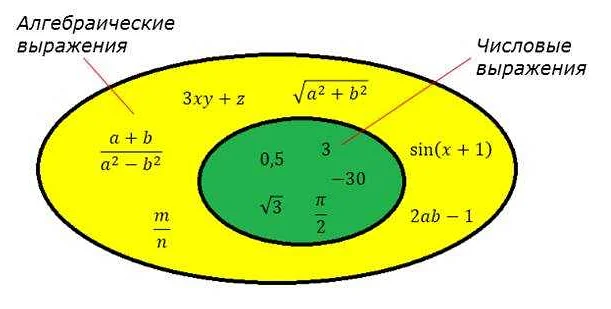
Сложные выражения могут содержать различные математические операции, такие как сложение, вычитание, умножение и деление, а также возведение в степень, извлечение корня и другие. Они могут также включать переменные, которые представляют неизвестные значения.

Сложные выражения могут быть использованы для решения различных математических задач, моделирования реальных ситуаций и выполнения вычислений. Они позволяют комбинировать различные операции и переменные для получения нужного результата.

У сложных выражений есть определенные свойства, которые помогают в их анализе и упрощении. Некоторые из основных свойств сложных выражений:

1. Ассоциативность — порядок выполнения операций не влияет на результат. Например, для сложения и умножения выполняется свойство ассоциативности: (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).
2. Коммутативность — порядок элементов не влияет на результат. Например, для сложения и умножения выполняется свойство коммутативности: a + b = b + a и a * b = b * a.
3. Распределительный закон — умножение распределено относительно сложения. Например, a * (b + c) = (a * b) + (a * c).
4. Идентичность — существует элемент, который не меняет результат операции. Например, для сложения и умножения идентичными элементами являются 0 и 1 соответственно.
5. Обратный элемент — для каждого элемента существует обратный элемент, который при операции даёт идентичность. Например, обратным элементом для сложения является противоположное число, а для умножения — обратное число.

Понимание определения и свойств сложных выражений поможет вам лучше разобраться в математических вычислениях и использовать их для решения различных задач.

Операторы и функции в сложном выражении

Операторы в сложном выражении выполняют математические операции, такие как сложение, вычитание, умножение и деление. Например, оператор «+» используется для сложения, оператор «-» — для вычитания, оператор «*» — для умножения, а оператор «/» — для деления. Эти операторы могут быть использованы в различных комбинациях для создания более сложных выражений.

Функции в сложном выражении выполняют специальные математические операции или действия. Например, функция «sin(x)» возвращает синус угла x, функция «cos(x)» возвращает косинус угла x, а функция «sqrt(x)» возвращает квадратный корень из числа x. Эти функции могут быть использованы для выполнения более сложных математических вычислений.

Примеры сложных выражений с операторами и функциями:

ВыражениеОписание

3 + 5	Сложение чисел 3 и 5
2 * 4	Умножение чисел 2 и 4
sqrt(9)	Квадратный корень из числа 9
sin(0)	Синус угла 0

Операторы и функции могут быть комбинированы в сложных выражениях для выполнения более сложных математических операций. Например, выражение «2 * sqrt(16)» умножает число 2 на квадратный корень из числа 16, что равно 8.

Понимание операторов и функций в сложном выражении позволяет нам создавать и анализировать математические вычисления. Они играют важную роль в различных областях, таких как физика, экономика и компьютерные науки.

Переменные и константы в сложном выражении

В сложном выражении переменные и константы могут быть комбинированы с помощью различных математических операций, таких как сложение, вычитание, умножение и деление. Например, выражение «2x + 3» содержит переменную «x» и константы «2» и «3», а также операцию сложения и умножения.

Переменные в сложном выражении могут принимать различные значения, в зависимости от контекста. Например, в выражении «2x + 3», значение переменной «x» может быть любым числом. Подстановка конкретных значений переменных в выражение позволяет вычислить его значение.

Константы, с другой стороны, имеют фиксированное значение, которое не изменяется в рамках выражения. Например, в выражении «2x + 3», константы «2» и «3» имеют фиксированное значение и не зависят от значения переменной «x».

Таким образом, переменные и константы играют важную роль в сложном выражении, представляя неизвестные и известные значения соответственно. Их комбинация с помощью математических операций позволяет строить сложные выражения и решать различные задачи в математике и других науках.

Приоритеты операций в сложном выражении

При выполнении математических операций в сложном выражении существуют определенные приоритеты, которые нужно учитывать.

В математике существуют следующие приоритеты операций:

• Сначала выполняются операции в скобках, так как они имеют наивысший приоритет.
• Затем выполняются операции с выражениями, содержащими степени и корни.
• После этого выполняются операции умножения и деления, которые имеют одинаковый приоритет.
• В конце выполняются операции сложения и вычитания, которые также имеют одинаковый приоритет.

Если в выражении присутствуют операции с одинаковым приоритетом, то они выполняются слева направо.

Например, в выражении 3 + 4 * 2 — 1 сначала выполняется умножение 4 * 2, затем сложение 3 + 8, и в конце вычитание 11 — 1, что дает результат 10.

Важно помнить о приоритетах операций при решении сложных выражений, чтобы получить правильный ответ.

Примеры сложных выражений с одним оператором

Сложное выражение в математике представляет собой выражение, состоящее из нескольких операндов, связанных одним оператором. В данном случае рассмотрим примеры сложных выражений с одним оператором.

Пример 1:

Вычислим значение выражения 3 + 2 + 4 + 1. Здесь оператором является сложение, а операндами — числа 3, 2, 4 и 1. Сложив все эти числа, получим результат: 10.

Пример 2:

Рассмотрим выражение 5 * 3 * 2 * 4. В данном случае оператором является умножение, а операндами — числа 5, 3, 2 и 4. Умножив все эти числа, получим результат: 120.

Пример 3:

Пусть дано выражение 10 — 4 — 2 — 1. Оператором здесь является вычитание, операндами — числа 10, 4, 2 и 1. Выполнив последовательное вычитание, получим результат: 3.

Таким образом, сложные выражения с одним оператором позволяют объединить несколько операндов в одну математическую операцию, которую можно вычислить для получения конечного результата.

Примеры сложных выражений с несколькими операторами

Сложные выражения в математике могут содержать несколько операторов, таких как сложение, вычитание, умножение и деление. Рассмотрим несколько примеров таких выражений:

1. Выражение 3 + 4 * 5 — 2 содержит операторы сложения, умножения и вычитания. Сначала выполняется умножение: 4 * 5 = 20. Затем сложение: 3 + 20 = 23. И наконец, вычитание: 23 — 2 = 21.
2. Выражение (8 + 2) / (4 — 2) содержит операторы сложения, вычитания и деления. Сначала выполняются операции в скобках: 8 + 2 = 10 и 4 — 2 = 2. Затем деление: 10 / 2 = 5.
3. Выражение 2 * (3 + 4) — 6 / 2 содержит операторы умножения, сложения, вычитания и деления. Сначала выполняется операция в скобках: 3 + 4 = 7. Затем умножение: 2 * 7 = 14. И наконец, деление и вычитание: 6 / 2 = 3 и 14 — 3 = 11.

Это лишь некоторые примеры сложных выражений с несколькими операторами. Математика предлагает бесконечное множество комбинаций, которые могут быть использованы для создания еще более сложных выражений.

Вопрос-ответ:

Что такое сложное выражение в математике?

Сложное выражение в математике представляет собой математическое выражение, содержащее несколько операций и переменных.

Какие операции могут содержаться в сложном выражении?

Сложное выражение может содержать операции сложения, вычитания, умножения, деления, возведения в степень, а также функции и операторы.

Какие переменные могут содержаться в сложном выражении?

Сложное выражение может содержать различные математические переменные, которые представляют значения, подлежащие вычислению.

Какие примеры сложных выражений можно привести?

Примерами сложных выражений могут быть: «2x + 3y», «4(x — 2) + 5y», «sin(x) + cos(y)», «a^2 + b^2 — 2ab», «log(x) / ln(y)», «sqrt(x^2 + y^2)».

Решение сложных выражений с помощью скобок

В математике сложные выражения могут содержать различные операции и числа. Чтобы правильно решить такие выражения, нужно использовать скобки.

Скобки позволяют установить порядок выполнения операций. Выражения внутри скобок всегда рассматриваются в первую очередь. Внутри скобок также могут быть другие скобки, и их порядок выполнения определяется изнутри наружу. Например, в выражении (2 + 3) * 4, сначала выполняется операция внутри скобок (2 + 3), а затем результат умножается на 4.

Скобки могут быть разных видов: круглые (), квадратные [], фигурные {}. Обычно круглые скобки используются для обозначения арифметических операций, квадратные — для обозначения массивов или матриц, а фигурные — для обозначения множеств.

При решении сложных выражений с помощью скобок следует придерживаться следующих правил:

• Выполняйте операции внутри скобок первыми.
• При наличии нескольких скобок сначала решайте выражения внутри самых внутренних скобок.
• Следуйте основным правилам математики: умножение и деление выполняются перед сложением и вычитанием.

Например, рассмотрим выражение: 2 * (3 + 4) — (5 — 2) * 6. Сначала решим выражения внутри скобок: (3 + 4) и (5 — 2). Получим: 2 * 7 — 3 * 6. Затем выполняем умножение и вычитание: 14 — 18. Итоговый ответ: -4.

Использование скобок в решении сложных выражений позволяет установить порядок выполнения операций и получить правильный результат.

Видео по теме: