Что такое смешанные числа 6 класс в математике

Смешанные числа в математике – это числа, состоящие из целой и десятичной части, которые обычно используются для представления нецелых значений. В 6 классе учатся работать с смешанными числами, выполнять операции сложения, вычитания, умножения и деления с ними. Узнайте, как правильно записывать и решать задачи с смешанными числами в данной статье.

Смешанные числа — это числа, которые состоят из целой и дробной частей. Они используются для представления нецелых величин, которые не могут быть выражены только с помощью десятичных дробей. В шестом классе в математике смешанные числа изучаются как важная составляющая десятичной системы счисления.

Основная особенность смешанных чисел заключается в том, что они позволяют нам представлять нецелые величины более точно. В смешанном числе целая часть записывается перед дробной частью, разделяя их знаком целочисленного деления, чаще всего дробью или запятой.

Например, смешанное число 3 1/2 представляет собой сумму целого числа 3 и дроби 1/2. Это означает, что у нас есть 3 целые единицы и еще половина целой единицы. Таким образом, смешанное число позволяет нам точно представить нецелую величину, которая находится между двумя целыми числами.

В шестом классе ученики изучают операции с смешанными числами, такие как сложение, вычитание, умножение и деление. Они также учатся приводить смешанные числа к общему знаменателю и сокращать дроби в смешанных числах. Изучение смешанных чисел помогает ученикам развивать навыки работы с десятичными числами и понимать их представление на числовой оси.

В заключение, смешанные числа играют важную роль в математике шестого класса. Они помогают ученикам более точно представлять нецелые величины и развивать навыки работы с десятичными числами. Изучение смешанных чисел является важным шагом в понимании десятичной системы счисления и подготовке к более сложным математическим концепциям.

Определение смешанных чисел 6 класс

Например, число 3+1/2 является смешанным числом. Здесь целая часть равна 3, а дробная часть – 1/2. Такое число можно интерпретировать как 3 целых единицы плюс половина единицы.

Смешанные числа обычно представляются в виде обыкновенных дробей. Например, число 3+1/2 можно записать как 7/2.

Смешанные числа широко используются в повседневной жизни, например, при измерении времени или расстояния.

Видео по теме:

Правила записи смешанных чисел

Смешанное число представляет собой комбинацию целой части и дробной части. Для правильной записи смешанного числа необходимо соблюдать определенные правила:

1. Целая часть отделяется от дробной части с помощью десятичной запятой или точки. Например: 4,5 или 4.5.

2. Целая часть записывается перед дробной частью. Например: 4,5 или 4.5.

3. Если смешанное число имеет целую часть равную нулю, то перед дробной частью ставится ноль. Например: 0,3 или 0.3.

4. В записи смешанного числа можно использовать пробелы для удобочитаемости. Например: 3 1/2 или 3 1/2.

5. Если смешанное число имеет целую часть и дробную часть равные нулю, то запишите только ноль. Например: 0 или 0.

При соблюдении указанных правил записи смешанных чисел становится удобной и понятной для чтения и работы с ними.

Перевод смешанных чисел в неправильные дроби

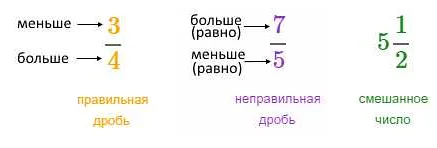
Смешанные числа состоят из целой части и дробной части, разделенных знаком «или». Для выполнения операций с смешанными числами удобно перевести их в неправильные дроби.

Чтобы перевести смешанное число в неправильную дробь, нужно:

1.	Умножить целую часть на знаменатель дробной части.
2.	Прибавить полученное произведение к числителю дробной части.
3.	Полученное число станет числителем новой неправильной дроби, а знаменателем останется тот же.

Например, для перевода смешанного числа 3 и 1/4 в неправильную дробь:

1. Умножаем целую часть (3) на знаменатель дробной части (4), получаем 3 * 4 = 12.

2. Прибавляем произведение (12) к числителю дробной части (1), получаем 12 + 1 = 13.

3. Полученная дробь будет выглядеть как 13/4.

Таким образом, смешанное число 3 и 1/4 равно неправильной дроби 13/4.

Перевод неправильных дробей в смешанные числа

Смешанное число — это число, которое состоит из целой части и дробной части. Например, число 3 1/2 является смешанным числом, потому что оно состоит из целой части 3 и дробной части 1/2.

Чтобы перевести неправильную дробь в смешанное число, нужно разделить числитель на знаменатель. Целая часть смешанного числа будет равна результату деления, а дробная часть будет состоять из остатка от деления и знаменателя. Например, чтобы перевести неправильную дробь 7/4 в смешанное число, мы делим 7 на 4. Результат деления равен 1 целой части и 3/4 дробной части. Таким образом, неправильная дробь 7/4 равна смешанному числу 1 3/4.

Таблица ниже показывает примеры перевода неправильных дробей в смешанные числа:

Неправильная дробьСмешанное число

5/2	2 1/2
9/3	3
11/4	2 3/4

Сложение смешанных чисел

Пример:

• Дано: 3 1/2 + 2 3/4
• Сначала складываем целые части: 3 + 2 = 5
• Затем складываем дробные части: 1/2 + 3/4 = 2/4 + 3/4 = 5/4
• Получаем результат: 5 1/4

Таким образом, смешанное число 3 1/2 плюс смешанное число 2 3/4 равно 5 1/4.

Вычитание смешанных чисел

1. Привести оба числа к общему знаменателю, умножив целую часть каждого смешанного числа на знаменатель и прибавив числитель. Полученные дроби будут иметь одинаковый знаменатель.

2. Вычесть числители полученных дробей и записать разность.

3. Если получившаяся разность является несократимой дробью, можно оставить ее в таком виде. Если же разность можно сократить, необходимо выполнить эту операцию.

Для более наглядного представления вычитания смешанных чисел можно использовать таблицу:

МинуендВычитаемоеРазность

Целая часть	Целая часть	Целая часть
Числитель	Числитель	Числитель
Знаменатель	Знаменатель	Знаменатель

Например, если нужно вычесть 2 3/4 из 5 1/2, то первым шагом приводим числа к общему знаменателю, который равен 4:

5 1/2 = 5 * 4/2 * 4 + 1 = 20/4 + 1 = 21/4

2 3/4 = 2 * 4/4 * 4 + 3 = 8/4 + 3 = 11/4

Затем вычитаем числители:

21/4 — 11/4 = (21 — 11)/4 = 10/4

Данная разность можно сократить:

10/4 = 5/2 = 2 1/2

Таким образом, 5 1/2 — 2 3/4 = 2 1/2.

Умножение смешанных чисел

Умножение смешанных чисел осуществляется следующим образом:

1. Произведение целой части чисел умножается на вторую дробь.

2. Произведение дробной части чисел умножается на первую дробь.

3. Полученные произведения складываются.

Пример:

Первое числоВторое числоПроизведение

3 1/2

2 3/4

(3 x 2) + (1/2 x 2) + (3/2 x 3/4) = 6 + 1 + 9/8 = 7 1/8

Деление смешанных чисел

1. Преобразовать оба смешанных числа в обыкновенные дроби.
2. Выполнить деление обыкновенных дробей.
3. Если результат деления обыкновенных дробей является неправильной дробью, то преобразовать ее обратно в смешанное число.

Пример:

Дано: 3 1/2 ÷ 1 2/3

Шаг 1: Преобразуем смешанные числа в обыкновенные дроби:

3 1/2 = (3 * 2 + 1) / 2 = 7/2

1 2/3 = (1 * 3 + 2) / 3 = 5/3

Шаг 2: Выполняем деление обыкновенных дробей:

(7/2) ÷ (5/3) = (7/2) * (3/5) = 21/10

Шаг 3: Проверяем результат и преобразуем его обратно в смешанное число:

21/10 = 2 1/10

Ответ: 3 1/2 ÷ 1 2/3 = 2 1/10

Таким образом, деление смешанных чисел выполняется путем преобразования их в обыкновенные дроби, выполнения деления этих дробей и, при необходимости, преобразования результата обратно в смешанное число.

Вопрос-ответ:

Что такое смешанные числа в математике?

Смешанные числа — это числа, которые состоят из целой части и дробной части, записанных вместе. Например, 3 1/2 или 4 3/4.

Как определить целую часть смешанного числа?

Целая часть смешанного числа — это целое число перед дробной частью. Например, в числе 3 1/2 целая часть равна 3.

Как определить дробную часть смешанного числа?

Дробная часть смешанного числа — это часть числа после целой части. Она записывается в виде обыкновенной дроби. Например, в числе 3 1/2 дробная часть равна 1/2.

Можете привести примеры смешанных чисел?

Конечно! Вот несколько примеров смешанных чисел: 2 3/4, 5 2/3, 7 1/5. В этих числах целая часть равна 2, 5 и 7 соответственно, а дробная часть — 3/4, 2/3 и 1/5.

Зачем нужны смешанные числа?

Смешанные числа используются, когда нужно записать число, которое больше целого, но меньше следующего целого числа. Они удобны для представления неполных частей или долей целого числа.

Что такое смешанные числа в математике?

Смешанные числа — это числа, которые состоят из целой части и дробной части. Например, 3 1/2 или 4 3/4.