Что такое сумма корней в математике
Содержимое
- 1 Что такое сумма корней в математике
- 1.1 Сумма корней в математике: общее понятие и применение
- 1.2 Что такое корень в математике?
- 1.3 Какие виды корней существуют?
- 1.4 Сумма корней: определение и особенности
- 1.5 Как вычислить сумму корней?
- 1.6 Примеры вычисления суммы корней
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Зачем нужно считать сумму корней в математике?
- 1.8.0.2 Как считается сумма корней квадратного уравнения?
- 1.8.0.3 Как считается сумма корней кубического уравнения?
- 1.8.0.4 Может ли сумма корней быть отрицательной?
- 1.8.0.5 Может ли сумма корней быть равна нулю?
- 1.8.0.6 Зачем нужно считать сумму корней в математике?
- 1.9 Сумма корней в квадратных уравнениях
- 1.10 Практическое применение суммы корней
Сумма корней в математике — это результат сложения всех корней уравнения или выражения. Узнайте, как найти сумму корней и как она связана с коэффициентами и степенями уравнения. Познакомьтесь с примерами и приложениями этого понятия в различных областях математики.
Сумма корней – это понятие, которое используется в математике для описания суммы всех корней уравнения. Корни уравнения являются значениями переменной, при которых уравнение становится истинным. Сумма корней может иметь важное значение при решении уравнений и в практической математике.
Сумма корней является одним из свойств уравнения и может быть положительной, отрицательной или нулевой. Знание суммы корней позволяет лучше понять характеристики и свойства уравнения, а также может быть использовано в дальнейших вычислениях или анализе данных.
Например, рассмотрим квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c – коэффициенты уравнения. Сумма корней в этом случае может быть выражена как S = -b/a. Это выражение позволяет нам найти сумму корней, не зная их точных значений, а только зная значения коэффициентов уравнения.
Знание понятия и свойств суммы корней является важным компонентом для понимания и решения уравнений в математике. Оно может быть применено в различных областях, таких как физика, экономика, инженерия и других, где уравнения являются неотъемлемой частью анализа данных и прогнозирования.
Сумма корней в математике: общее понятие и применение
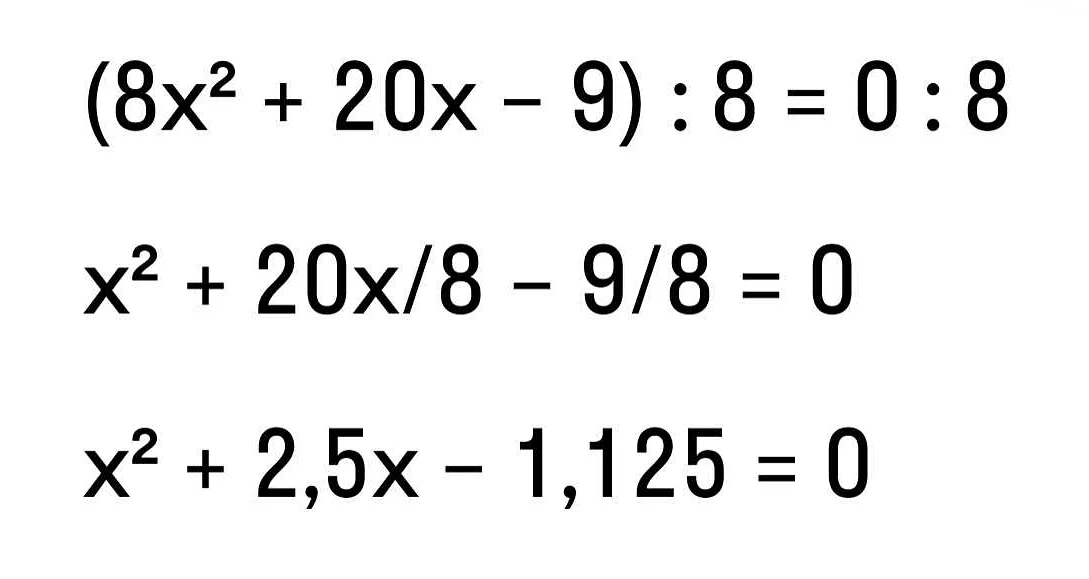
Сумма корней может быть полезна в различных областях математики и ее приложениях. Например, в алгебре сумма корней может помочь упростить выражение или найти решение уравнения. В геометрии сумма корней может использоваться для нахождения суммарного значения углов в многоугольнике или при решении задач на подобие фигур. В физике сумма корней может помочь определить значения переменных в уравнениях движения или решить задачи на определение скорости, ускорения и других физических величин.
Примером задачи, где требуется найти сумму корней, может быть уравнение вида:
x^2 + 4x — 5 = 0
Для нахождения корней этого уравнения можно воспользоваться формулой дискриминанта:
D = b^2 — 4ac
где a, b и c – коэффициенты уравнения. В данном примере a = 1, b = 4 и c = -5.
Если дискриминант больше нуля, то у уравнения есть два корня, которые можно найти по формуле:
x1 = (-b + √D) / (2a)
x2 = (-b — √D) / (2a)
Если дискриминант равен нулю, то у уравнения есть один корень, который можно найти по формуле:
x = -b / (2a)
Таким образом, сумма корней уравнения x^2 + 4x — 5 = 0 будет равна x1 + x2.
Что такое корень в математике?
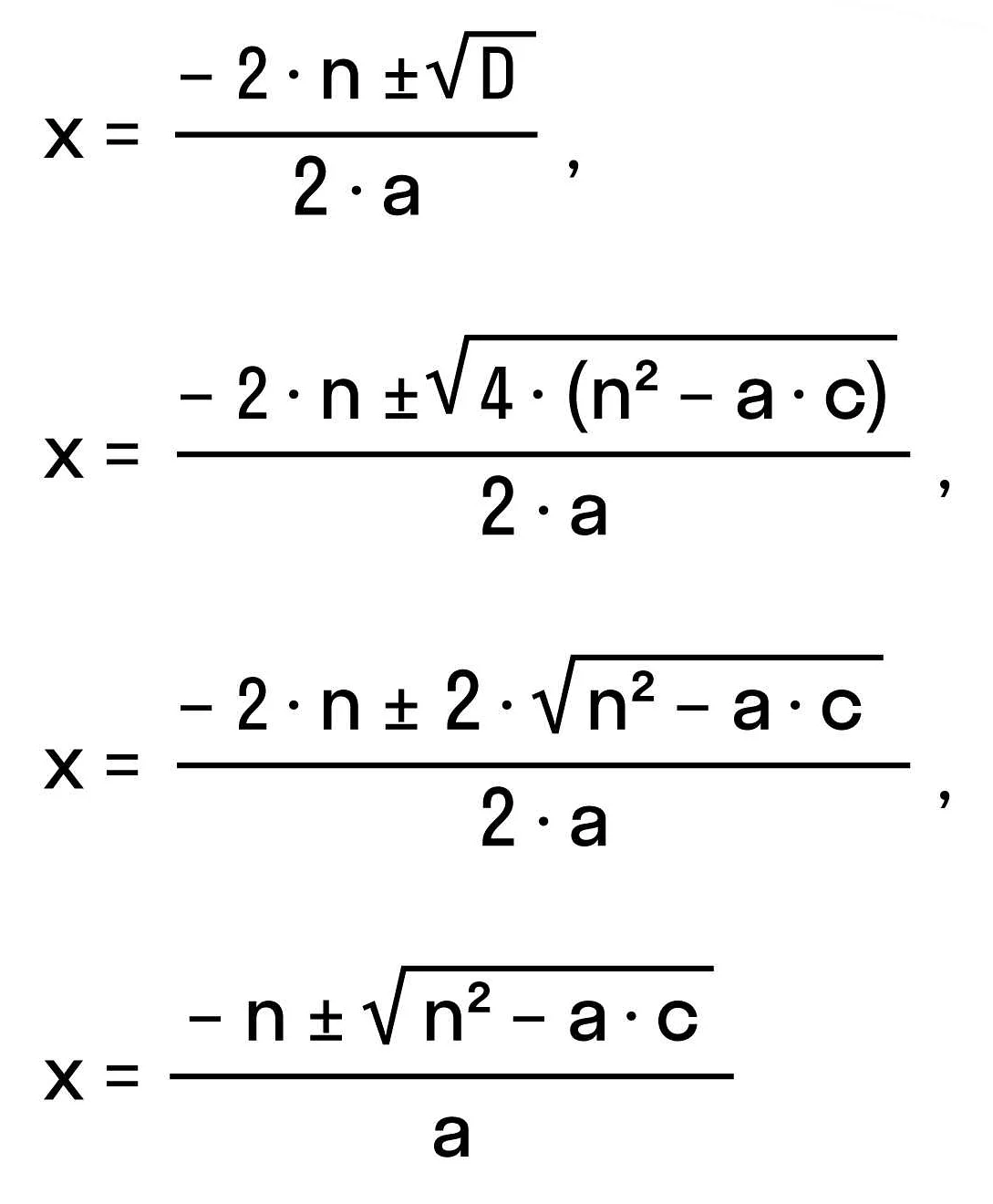
Например, корень квадратный из числа 9 равен 3, так как 3^2 = 9. Корень кубический из числа 8 равен 2, так как 2^3 = 8.
Корни могут быть как положительными, так и отрицательными. Например, корень квадратный из числа 16 может быть равен как 4, так и -4, так как и 4^2 = 16, и (-4)^2 = 16.
Корни в математике широко используются при решении уравнений, вычислении площадей и объемов геометрических фигур, а также в других областях науки и техники.
Какие виды корней существуют?

В математике существует несколько видов корней, которые используются в различных областях и задачах.
1. Квадратный корень
Квадратный корень это операция, обратная возведению числа в квадрат. Квадратный корень из числа а обозначается символом √a. Результатом извлечения квадратного корня из числа а является число b, такое что b^2 = a. Например, квадратный корень из 9 равен 3, так как 3^2 = 9.
2. Кубический корень
Кубический корень это операция, обратная возведению числа в куб. Кубический корень из числа а обозначается символом √3a. Результатом извлечения кубического корня из числа а является число b, такое что b^3 = a. Например, кубический корень из 8 равен 2, так как 2^3 = 8.
3. Натуральный корень
Натуральный корень это операция, обратная возведению числа в натуральную степень. Натуральный корень из числа а обозначается символом √na, где n — натуральное число. Результатом извлечения натурального корня из числа а является число b, такое что b^n = a. Например, натуральный корень второй степени из 25 равен 5, так как 5^2 = 25.
4. Рациональный корень
Рациональный корень это операция, обратная возведению числа в рациональную степень. Рациональный корень из числа а обозначается символом √m/na, где m и n — рациональные числа. Результатом извлечения рационального корня из числа а является число b, такое что b^(m/n) = a. Например, рациональный корень третьей степени из 64 равен 4, так как 4^(1/3) = 64.
5. Иррациональный корень
Иррациональный корень это корень, который не может быть представлен в виде десятичной дроби или дроби. Например, корень из числа 2 является иррациональным числом. Его значение приближенно равно 1.41421356 и так далее. Иррациональные корни обозначаются символом √a.
Знание различных видов корней поможет в решении различных математических задач и понимании математических концепций.
Сумма корней: определение и особенности
Для уравнения вида ax^2 + bx + c = 0, где a, b и c — это коэффициенты, сумма корней может быть найдена с использованием формулы:
S = -b/a
В случае квадратного уравнения, сумма корней будет равна -b/a. Это означает, что сумма корней равна отрицательному коэффициенту при x, деленному на коэффициент при x^2.
Особенностью суммы корней является то, что она может быть использована для определения некоторых свойств уравнения. Например, если сумма корней равна нулю, то это означает, что уравнение имеет один корень или два равных корня. Если сумма корней отрицательна, то уравнение имеет два различных корня. Если сумма корней положительна, то уравнение также имеет два различных корня.
Таблица ниже показывает примеры расчета суммы корней для нескольких уравнений:
УравнениеСумма корней
| x^2 + 4x + 3 = 0 | -4 |
| 2x^2 — 5x + 2 = 0 | 5/2 |
| 3x^2 + 2x + 1 = 0 | -2/3 |
Таким образом, сумма корней является важным показателем, который помогает понять свойства уравнения и решить его.
Как вычислить сумму корней?
Один из способов вычисления суммы корней — это использование формулы Виета для квадратного уравнения. Для квадратного уравнения вида ax^2 + bx + c = 0, сумма корней может быть найдена как сумма обоих корней x1 и x2, которая равна -b/a.
Другой способ вычисления суммы корней — это использование теоремы Виета для общего полинома. Теорема Виета утверждает, что сумма корней полинома равна коэффициенту x^(n-1) / a_n-1, где n — степень полинома, а a_n-1 — коэффициент при x^(n-1).
Также можно использовать метод суммирования рекуррентных формул для вычисления суммы корней. Например, для квадратного уравнения можно использовать формулу суммы корней x1 + x2 = -b/a, а для кубического уравнения — формулу x1 + x2 + x3 = -b/a, где b — коэффициент при x в уравнении.
В зависимости от конкретной задачи и доступных данных, можно выбрать наиболее подходящий метод для вычисления суммы корней. Важно учитывать, что вычисление суммы корней может помочь в решении различных задач, связанных с математикой, физикой и другими науками.
Примеры вычисления суммы корней

Рассмотрим несколько примеров, чтобы лучше понять, как вычислять сумму корней.
-
- Пример 1: Вычисление суммы корней квадратного уравнения
Дано квадратное уравнение: ax^2 + bx + c = 0. Чтобы найти сумму корней, нужно использовать формулу: x1 + x2 = -b/a, где x1 и x2 — корни уравнения. Например, для уравнения x^2 — 5x + 6 = 0, сумма корней будет: x1 + x2 = -(-5)/1 = 5/1 = 5.
-
- Пример 2: Вычисление суммы корней кубического уравнения
Дано кубическое уравнение: ax^3 + bx^2 + cx + d = 0. Чтобы найти сумму корней, нужно использовать формулу: x1 + x2 + x3 = -b/a, где x1, x2 и x3 — корни уравнения. Например, для уравнения x^3 — 6x^2 + 11x — 6 = 0, сумма корней будет: x1 + x2 + x3 = -(-6)/1 = 6/1 = 6.
-
- Пример 3: Вычисление суммы корней линейного уравнения
Дано линейное уравнение: ax + b = 0. Чтобы найти сумму корней, нужно решить уравнение и получить один корень. Например, для уравнения 2x + 3 = 0, сумма корней будет: x = -3/2.
Видео по теме:
Вопрос-ответ:
Зачем нужно считать сумму корней в математике?
Сумма корней является важным понятием в математике и используется для решения различных задач. Например, сумма корней квадратного уравнения может дать нам информацию о сумме значений переменной в этом уравнении. Также сумма корней может быть полезна при решении систем уравнений или при анализе графиков функций.
Как считается сумма корней квадратного уравнения?
Для нахождения суммы корней квадратного уравнения нужно просто сложить значения корней. Квадратное уравнение обычно имеет два корня, поэтому сумма корней будет равна сумме этих двух значений. Например, если у нас есть уравнение x^2 — 5x + 6 = 0, то его корни равны 2 и 3, и сумма корней будет равна 2 + 3 = 5.
Как считается сумма корней кубического уравнения?
Для нахождения суммы корней кубического уравнения нужно сложить значения корней. Кубическое уравнение обычно имеет три корня. Например, если у нас есть уравнение x^3 — 6x^2 + 11x — 6 = 0, то его корни равны 1, 2 и 3, и сумма корней будет равна 1 + 2 + 3 = 6.
Может ли сумма корней быть отрицательной?
Сумма корней может быть как положительной, так и отрицательной. В зависимости от уравнения и его корней, сумма может быть любым числом. Например, если у нас есть уравнение x^2 — 4x + 4 = 0, то его корни равны 2 и 2, и сумма корней будет равна 2 + 2 = 4, что является положительным числом.
Может ли сумма корней быть равна нулю?
Сумма корней может быть равна нулю, если один из корней равен нулю, а остальные корни равны противоположным числам друг другу. Например, если у нас есть уравнение x^3 — 6x^2 + 11x — 6 = 0, то его корни равны 1, 2 и 3, и их сумма равна 1 + 2 + 3 = 6. В этом случае сумма корней не равна нулю.
Зачем нужно считать сумму корней в математике?
Сумма корней в математике может быть полезной в различных задачах и исследованиях. Например, сумма корней может помочь определить сумму значений функции или решить уравнение.
Сумма корней в квадратных уравнениях
Сумма корней квадратного уравнения может быть найдена с использованием формулы суммы корней. Для квадратного уравнения ax^2 + bx + c = 0 с корнями x1 и x2 сумма корней равна -b/a.
Пример:
Рассмотрим квадратное уравнение 2x^2 — 5x + 2 = 0. Найдем корни данного уравнения.
Используя формулу дискриминанта, находим его значение: D = b^2 — 4ac = (-5)^2 — 4(2)(2) = 25 — 16 = 9.
Так как дискриминант положительный, уравнение имеет два действительных корня.
Применяем формулу для нахождения корней: x1 = (-b + √D) / (2a) = (5 + √9) / 4 = (5 + 3) / 4 = 2,
x2 = (-b — √D) / (2a) = (5 — √9) / 4 = (5 — 3) / 4 = 1/2.
Сумма корней равна: x1 + x2 = 2 + 1/2 = 2 1/2 = 5/2.
Таким образом, сумма корней в квадратных уравнениях может быть найдена с использованием формулы суммы корней, что позволяет получить важную информацию о свойствах уравнения и его корнях.
Практическое применение суммы корней
Кроме того, сумма корней может быть использована для расчета различных статистических показателей. Например, среднее арифметическое (среднее значение) набора чисел можно выразить через сумму корней и их количества. Другим важным применением является нахождение значения функции, если известны корни уравнения, задающего эту функцию.
Также сумма корней может использоваться в геометрии для нахождения координат точек пересечения графиков функций. Если заданы две функции, уравнения которых имеют корни, то координаты точек пересечения могут быть найдены через сумму корней уравнений.
Практическое применение суммы корней в математике позволяет решать различные задачи и находить значения неизвестных величин. Это важное понятие имеет широкий спектр применения и играет значительную роль в решении различных математических задач и проблем.
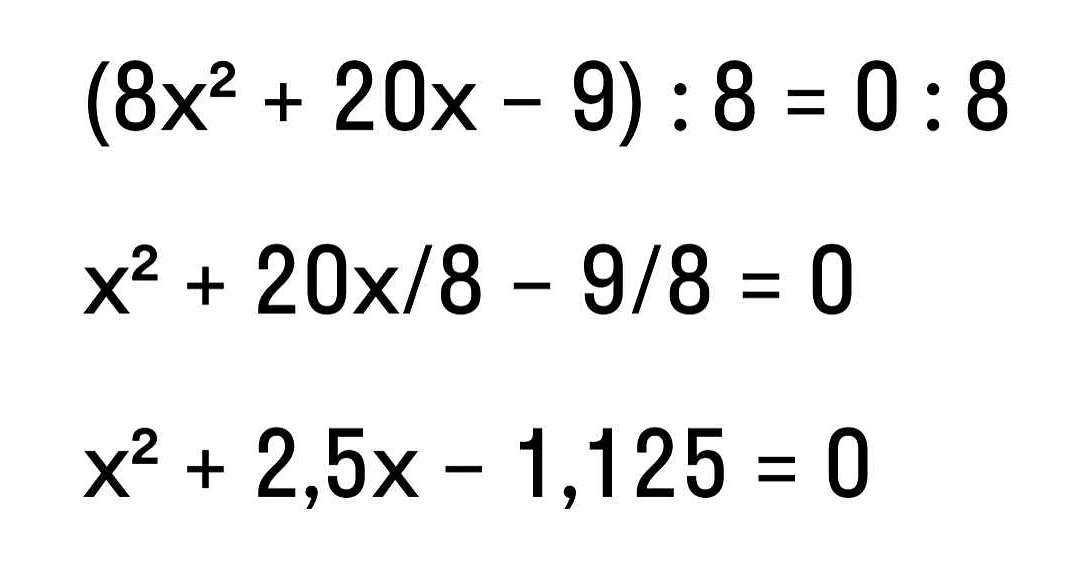




Уважаемый автор, благодарю вас за интересную статью на тему «Что такое сумма корней в математике: объяснение и примеры». Как читатель, мне было очень интересно узнать о данном математическом понятии. Ваше объяснение было понятным и легким для восприятия. Я особенно оценила примеры, которые вы привели, чтобы проиллюстрировать сумму корней. Это помогло мне лучше понять, как применять данное понятие на практике. Теперь я понимаю, что сумма корней — это сумма всех значений, которые удовлетворяют уравнению. Также хотелось бы отметить вашу ясную и систематическую структуру статьи. Вы начали с объяснения основных терминов и постепенно перешли к более сложным концепциям. Это помогло мне лучше понять материал и улучшило мою восприимчивость к теме. В целом, ваша статья была очень полезной и понятной. Я получила новые знания о сумме корней и теперь могу лучше разбираться в этой области математики. Спасибо за четкое объяснение и интересные примеры! Я с нетерпением жду новых статей от вас.
Статья очень понятно объясняет, что такое сумма корней в математике. Я всегда задавался вопросом, зачем нам нужны корни и как с ними работать. Теперь все стало ясно. Очень понравилось, что автор привел примеры, которые помогли мне лучше понять материал. Теперь я могу более уверенно решать задачи, связанные с суммой корней. Очень надеюсь, что в будущем автор напишет еще статей на подобные темы. Спасибо!