Что такое уравнение в математике

Уравнение в математике — это математическое выражение, которое содержит неизвестное значение или переменную. В уравнении подразумевается, что значение или переменная должны быть определены таким образом, чтобы соответствовать заданным условиям или равенству. Уравнения широко используются в различных областях математики и науки, а также в реальных приложениях, чтобы решить проблемы и найти неизвестные значения. Понимание уравнений является важной основой для развития математических навыков и решения сложных задач.

Уравнение — это математическое выражение, которое содержит как минимум одну переменную и знак равенства. Оно описывает равенство двух выражений и позволяет найти значения переменной, при которых это равенство выполняется. Уравнения являются фундаментальным понятием в математике и находят применение во многих областях науки и жизни.

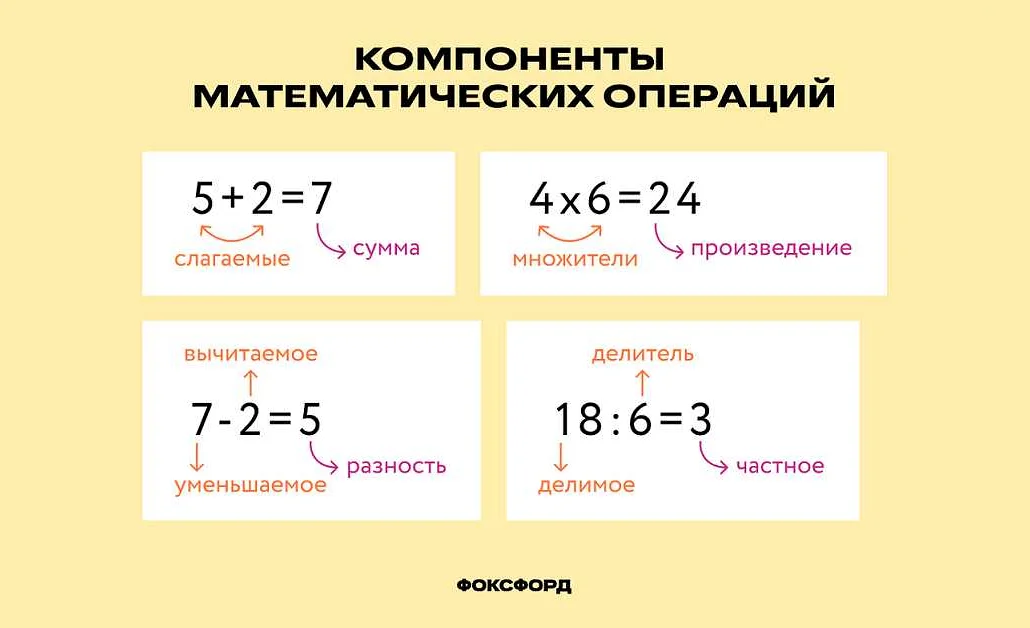
Основными понятиями, связанными с уравнениями, являются корень и степень уравнения. Корень уравнения — это значение переменной, при котором уравнение становится верным. Степень уравнения определяется как наивысшая степень переменной в уравнении. Например, уравнение вида 3x^2 — 2x + 1 = 0 имеет степень 2, так как переменная x возведена во вторую степень.

Уравнения могут быть линейными и квадратными, в зависимости от их степени. Линейные уравнения имеют степень 1 и имеют вид ax + b = 0, где a и b — константы. Квадратные уравнения имеют степень 2 и имеют вид ax^2 + bx + c = 0, где a, b и c — константы, а x — переменная.

Решение уравнений — это процесс нахождения всех значений переменной, при которых уравнение становится верным. Решение уравнения может быть аналитическим или численным. Аналитическое решение позволяет найти точные значения переменной, а численное решение предоставляет приближенные значения.

Что такое уравнение?

В уравнении есть две части: левая и правая. Левая часть содержит выражение, в котором используются известные числа и неизвестные. Правая часть содержит выражение, равное результату. Чтобы решить уравнение, нужно найти значения неизвестных, при которых левая часть равна правой.

Уравнения могут быть линейными или нелинейными. Линейные уравнения имеют степень 1, то есть в них отсутствуют степени переменных, кроме 1. Нелинейные уравнения имеют степень больше 1 и могут содержать различные математические операции, такие как возведение в степень, извлечение корня и другие.

Примеры уравнений:

Линейное уравнение: 2x + 3 = 9

Нелинейное уравнение: x^2 — 5x + 6 = 0

Решение уравнений — это нахождение значений неизвестных, при которых уравнение становится верным. Решение уравнения может быть одним или несколькими. Для решения уравнений используются различные методы, такие как подстановка, факторизация, приведение подобных членов и другие.

Какие основные понятия связаны с уравнением?

Основные понятия, связанные с уравнением:

1. Неизвестная — это величина, значение которой неизвестно и ищется в уравнении. Обозначается обычно буквой, например, x, y или z.
2. Известные величины — это величины, значения которых уже известны и входят в уравнение. Они могут быть числами или другими переменными.
3. Коэффициенты — это числа, которые умножаются на неизвестную величину в уравнении. Коэффициенты могут быть положительными, отрицательными или нулевыми.
4. Степень — это показатель, определяющий количество раз, сколько нужно умножить неизвестную величину саму на себя. Например, в уравнении x^2 = 9, степень неизвестной величины x равна 2.
5. Решение уравнения — это значения неизвестной величины, при которых уравнение становится верным. Решение может быть одно или несколько, а также может быть бесконечно много.

Понимание этих основных понятий помогает в решении уравнений различной сложности и является основой для изучения более продвинутых тем в математике.

Примеры уравнений

1. Простое линейное уравнение: 2x + 3 = 7. В данном уравнении неизвестное значение обозначено буквой x. Необходимо найти значение x, при котором уравнение будет выполняться.

2. Квадратное уравнение: x^2 + 4x + 4 = 0. В данном уравнении неизвестное значение также обозначено буквой x. Необходимо найти значение x, при котором уравнение будет выполняться и равенство будет верным.

3. Система уравнений:

2x + y = 10

x — y = 2

. В данном примере есть два уравнения с двумя неизвестными значениями x и y. Необходимо найти значения x и y, при которых оба уравнения будут выполняться и равенства будут верными.

Это лишь некоторые примеры уравнений, которые могут возникать в математике. Уравнения широко применяются в различных областях, включая физику, экономику, инженерию и т. д.

Как решать уравнения?

Одним из методов решения уравнений является метод подстановки. Он заключается в последовательной замене неизвестной переменной значениями из диапазона, заданного условием уравнения. Подставляя значения и проверяя, выполняется ли уравнение, можно найти корни уравнения.

Другим распространенным методом решения уравнений является метод факторизации. Он применяется к уравнениям, которые можно представить в виде произведения двух или более множителей. Разложив уравнение на множители и приравняв каждый множитель к нулю, можно найти значения переменных, удовлетворяющие уравнению.

Еще одним методом решения уравнений является метод дискриминанта. Он применяется к уравнениям второй степени и основан на вычислении дискриминанта, который позволяет определить тип корней уравнения. Зная значение дискриминанта, можно найти корни уравнения.

Существуют и другие методы решения уравнений, такие как метод графиков, метод итераций и методы численного решения. Каждый из методов имеет свои особенности и применяется в зависимости от типа и сложности уравнения.

Важно понимать, что для успешного решения уравнений необходимо знание основ математики, включая алгебру, арифметику и логику. Также важно умение применять различные методы решения и выбирать наиболее подходящий для конкретного уравнения.

Линейное уравнение

ax + b = 0,

где a и b — коэффициенты, а x — переменная, подлежащая определению. Решение линейного уравнения — это значение переменной x, при котором уравнение выполняется.

Примеры линейных уравнений:

2x — 3 = 0

3y + 5 = 2y — 3

4z + 2 = 10

Решение линейных уравнений может быть найдено путем применения различных методов, таких как метод подстановки, метод исключения и метод графического представления. Решение линейных уравнений имеет важное значение в различных областях математики и физики, а также в прикладных науках и инженерии.

Квадратное уравнение

ax2 + bx + c = 0,

где a, b и c – известные числа, а x – неизвестная. Коэффициент a не может быть равным нулю.

Решение квадратного уравнения может быть найдено с использованием формулы:

x = (-b ± √(b2 — 4ac)) / 2a.

Если значение дискриминанта (D = b2 — 4ac) равно нулю, то уравнение имеет одно решение. Если D больше нуля, то уравнение имеет два различных решения. Если D меньше нуля, то уравнение не имеет решений в области действительных чисел.

Примеры квадратных уравнений:

УравнениеРешение

x2 — 5x + 6 = 0	x1 = 2, x2 = 3
2×2 + 3x — 2 = 0	x1 = -2, x2 = 0.5
3×2 + 4x + 2 = 0	Нет решений

Системы уравнений

Система уравнений представляет собой набор нескольких уравнений, которые должны быть решены одновременно. В основном, системы уравнений используются для моделирования различных физических и математических задач.

Система уравнений может быть линейной или нелинейной. В линейной системе уравнений все уравнения являются линейными, то есть степени переменных в уравнениях не превышают первой степени. Нелинейная система уравнений содержит хотя бы одно уравнение с переменными степенями более первой.

Решение системы уравнений — это набор значений переменных, который удовлетворяет всем уравнениям системы. Решениями могут быть как числа, так и бесконечные множества значений. В зависимости от числа решений системы уравнений, она может быть разрешимой, неразрешимой или иметь бесконечное количество решений.

Системы уравнений могут быть решены различными методами, такими как метод подстановки, метод исключения и метод графического представления. Выбор метода решения зависит от сложности системы и требуемой точности результата.

Одним из примеров системы уравнений является система уравнений с двумя неизвестными:

2x + 3y = 7

4x — 2y = 2

Для решения этой системы уравнений можно использовать, например, метод исключения или метод подстановки.

Вопрос-ответ:

Что такое уравнение в математике?

Уравнение в математике — это математическое выражение, содержащее неизвестные значения, которые нужно найти, и символ равенства.

Какие основные понятия связаны с уравнением?

Основными понятиями, связанными с уравнением, являются неизвестная величина (или неизвестные величины), коэффициенты, степень уравнения, корни уравнения и решение уравнения.

Какие примеры уравнений существуют?

Примеры уравнений могут включать линейные уравнения, квадратные уравнения, уравнения с рациональными выражениями, тригонометрические уравнения, логарифмические уравнения и другие.

Как решать уравнения?

Для решения уравнений применяются различные математические методы, такие как подстановка, факторизация, извлечение корней, использование формул и т.д. В зависимости от типа уравнения и его сложности выбирается соответствующий метод решения.

Зачем нужны уравнения в математике?

Уравнения в математике являются мощным инструментом для моделирования и решения различных задач. Они позволяют находить неизвестные значения, определять зависимости между величинами, решать задачи из различных областей науки, техники, экономики и других сфер жизни.

Какое определение уравнения в математике?

Уравнение в математике — это математическое выражение, в котором присутствуют неизвестные величины, которые нужно найти, и известные величины, которые заданы. Оно представляет собой равенство двух выражений и используется для нахождения значений неизвестных величин.

Какие основные понятия связаны с уравнением в математике?

Основными понятиями, связанными с уравнением в математике, являются: неизвестные величины, известные величины, коэффициенты, степени, корни, решения. Неизвестные величины — это те величины, которые нужно найти. Известные величины — это те величины, которые заданы. Коэффициенты — это числа, умноженные на неизвестные величины. Степень — это показатель, в котором величина входит в уравнение. Корни — это значения неизвестных величин, при которых уравнение выполняется. Решения — это значения неизвестных величин, при которых уравнение выполняется.

Видео по теме: