Что такое сыс в математике

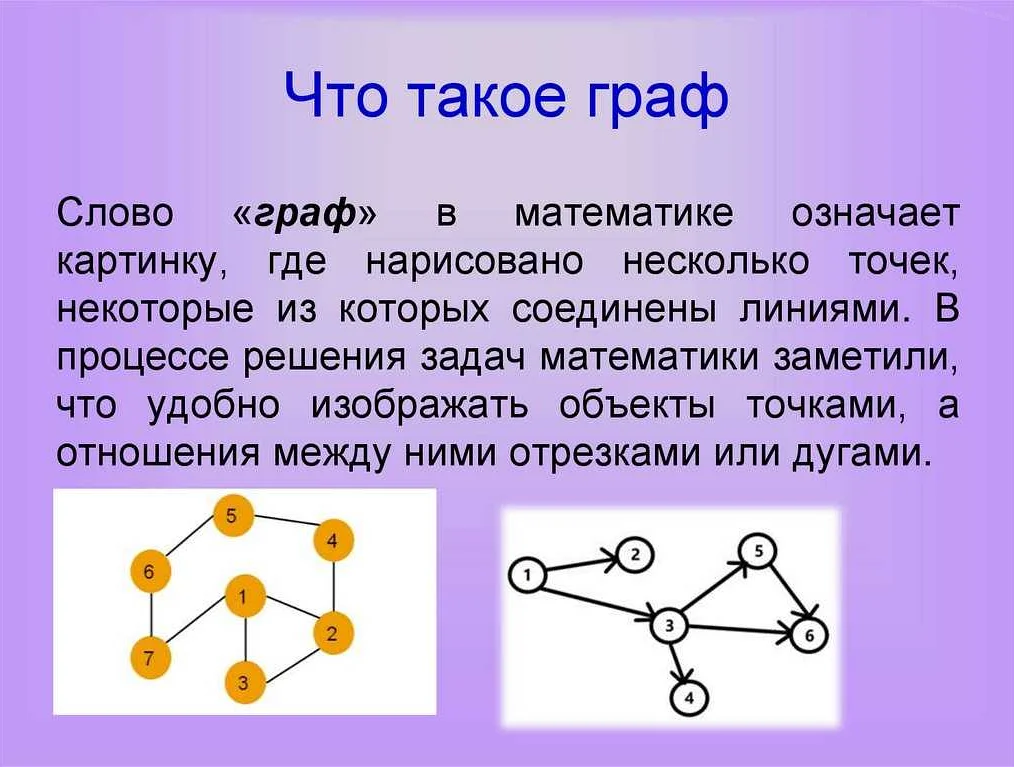
Сыс в математике является частным случаем графа, представляющего собой упорядоченное множество вершин и связей между этими вершинами. Сыс используется для моделирования и анализа сложных систем и процессов, таких как социальные сети, транспортные сети, электрические цепи и другие. В данной статье рассматривается понятие сыса, его свойства и применение в математике и реальном мире.

Сыс (от английского слова «система») — это термин, который используется в математике для обозначения набора взаимосвязанных компонентов, представляющих собой целостную структуру. Сыс может включать в себя различные элементы, такие как уравнения, функции, операции и т.д. Сыс является важным инструментом в математическом анализе и моделировании, позволяя упростить сложные задачи и решать их с помощью систематического подхода.

Одной из основных причин использования сыс в математике является возможность анализировать и прогнозировать поведение системы в различных условиях. Сыс позволяет устанавливать взаимосвязи между различными переменными и исследовать их взаимодействие. Например, сыс может быть использован для моделирования экономической системы, физического процесса или биологической популяции. Анализ сыс позволяет нам определить, какие факторы влияют на поведение системы и как они взаимодействуют друг с другом.

Пример использования сыс в математике: моделирование популяции животных

Допустим, мы хотим исследовать динамику популяции животных в определенной области. Мы можем использовать сыс, чтобы определить, как различные факторы, такие как доступность пищи, количество хищников и рождаемость, влияют на размер популяции животных. Мы можем разработать уравнения, описывающие изменение численности популяции во времени, и использовать их для прогнозирования будущего развития популяции.

Сыс также позволяет нам исследовать различные стратегии управления популяцией, такие как ограничение охоты на животных или введение новых видов в экосистему. Мы можем использовать сыс, чтобы определить, какие меры будут наиболее эффективными в сохранении популяции и предотвращении ее вымирания.

Понятие сыс в математике

Сыс может быть представлен в виде таблицы, где каждая строка представляет собой отдельный объект, а столбцы указывают на различные свойства или атрибуты этого объекта. Например, сыс может описывать набор студентов, где каждая строка представляет собой отдельного студента, а столбцы могут содержать информацию о его имени, возрасте, поле и т. д.

ИмяВозрастПол

Иван	25	Мужской
Анна	23	Женский
Петр	27	Мужской

В данном примере, сыс представляет собой набор студентов, каждый из которых имеет имя, возраст и пол. Такая структура данных может быть полезной, например, для хранения информации о студентах в учебной базе данных.

Примеры сыс в математике

Рассмотрим следующую систему уравнений:

• 2x + 3y = 7
• 4x — 5y = -3

Для решения этой системы уравнений методом Гаусса, мы можем записать расширенную матрицу:

(2 3 | 7)
(4 -5 | -3)

Затем мы применяем элементарные преобразования строк, чтобы привести матрицу к ступенчатому виду:

(1 0 | 17/11)
(0 1 | -5/11)

Таким образом, решением данной системы уравнений будет x = 17/11 и y = -5/11.

Это лишь один из примеров использования сыс в математике. Существуют и другие методы решения систем линейных уравнений с использованием сыс, такие как метод Крамера и метод прогонки.

Использование сыс в алгебре

Применение сыс в алгебре позволяет решать сложные математические задачи, связанные с нахождением неизвестных значений. Сыс позволяет свести систему уравнений или неравенств к одному уравнению или неравенству, что упрощает процесс решения и позволяет получить точные ответы.

Например, рассмотрим систему уравнений:

2x + 3y = 8

x — y = 2

С помощью сыс можно объединить эти два уравнения в одно:

2x + 3y = 8

2(x — y) = 2(2)

После объединения уравнений, мы можем решить полученное уравнение и найти значения переменных x и y.

Таким образом, использование сыс в алгебре является мощным инструментом для решения математических задач, связанных с системами уравнений и неравенств. Он позволяет упростить процесс решения и получить точные ответы.

Сыс и геометрия

В геометрии сыс используется для определения расстояния между двумя точками. Он может быть использован для измерения расстояния между двумя геометрическими фигурами, а также для нахождения длины отрезка или стороны фигуры.

Примеры использования сыса в геометрии включают нахождение длины отрезка между двумя точками на плоскости, нахождение расстояния от точки до прямой или плоскости, а также построение треугольников и других фигур.

• Нахождение длины отрезка между точками A и B: сыс AB.
• Нахождение расстояния от точки C до прямой AB: сыс СAB.
• Построение треугольника ABC, где сыс AB, BC и CA являются сторонами треугольника.

Сыс является фундаментальным понятием в геометрии и широко применяется в решении различных задач и построении геометрических фигур.

Сыс и анализ

Анализ, с другой стороны, это процесс разложения сложных объектов или проблем на более простые и понятные составляющие. В математике анализ используется для изучения функций, пределов, производных и интегралов.

Сыс и анализ тесно связаны друг с другом. Используя систему счисления, мы можем анализировать числа и выполнять различные операции над ними. Анализ, в свою очередь, позволяет нам понять особенности и закономерности, связанные с числами и их представлением в определенной системе счисления.

Например, при анализе чисел в десятичной системе счисления мы можем определить их разрядность, узнать, является ли число четным или нечетным, и так далее. Также, используя систему счисления, мы можем проводить анализ функций и находить их производные и интегралы, что позволяет нам изучать и понимать их свойства и поведение.

Таким образом, сыс и анализ взаимосвязаны и играют важную роль в математике, позволяя нам понять и работать с числами и функциями.

Видео по теме:

Вопрос-ответ:

Что такое сыс в математике?

Сыс (сокращение от слов «система счисления») — это способ представления чисел, который основан на определенной системе цифр и правилах их комбинирования.

Какие существуют примеры использования сыс в математике?

Примерами использования сыс в математике являются десятичная система счисления (основана на цифрах от 0 до 9), двоичная система счисления (основана на цифрах 0 и 1), восьмеричная система счисления (основана на цифрах от 0 до 7) и шестнадцатеричная система счисления (основана на цифрах от 0 до 9 и буквах A-F).

Какую роль играет сыс в математике?

Сыс играет важную роль в математике, так как позволяет нам представлять числа и выполнять математические операции с ними. Она также позволяет удобно записывать и обрабатывать числовую информацию в компьютерах.

Какие преимущества имеет использование сыс в математике?

Использование сыс в математике позволяет более компактно представлять числа, удобно выполнять математические операции, а также обрабатывать числовую информацию в компьютерных системах. Кроме того, различные системы счисления могут быть полезны для решения различных задач в разных областях науки и техники.

Можете привести примеры использования сыс в реальной жизни?

Одним из примеров использования сыс в реальной жизни может быть работа с IP-адресами в компьютерных сетях, которые представляются в виде четырех чисел, разделенных точками (например, 192.168.0.1). Также сыс используется в деньговом учете, где суммы могут записываться в виде десятичных дробей, а в некоторых странах деньги могут быть представлены в виде разных систем счисления (например, иены в Японии).

Что такое сыс в математике?

Сыс в математике — это обозначение для суммы, которая может иметь бесконечное число слагаемых.

Какие примеры использования сыса в математике?

Сыс используется, например, при вычислении суммы бесконечного ряда или при записи пределов функций.

Значение сыс в теории вероятностей

Вероятность сыс вычисляется с использованием формулы условной вероятности:

P(A|B) = P(A ∩ B) / P(B)

Где P(A|B) — вероятность наступления события A при условии, что событие B уже произошло; P(A ∩ B) — вероятность одновременного наступления событий A и B; P(B) — вероятность наступления события B.

Значение сыс в теории вероятностей позволяет рассчитывать вероятности сложных случайных событий, учитывая уже произошедшие события. Это особенно полезно при моделировании реальных ситуаций, где часто возникают зависимости между различными событиями.

Сыс в теории чисел

Сыс можно представить в виде a + b, где a и b — целые числа. Числа a и b могут быть как положительными, так и отрицательными. Важно отметить, что сыс обладает свойством коммутативности, то есть порядок слагаемых не имеет значения.

Сысы играют важную роль в различных областях математики. Например, в алгебре они используются для классификации чисел или элементов в кольцах. В теории чисел сысы могут быть полезны при решении некоторых задач, например, для нахождения суммы последовательности чисел или для нахождения решений диофантовых уравнений. Они также могут быть полезны при анализе свойств простых чисел или при изучении теоремы Вильсона.

Примеры использования сысов в теории чисел:

• Сумма двух сысов: (a + b) + (c + d) = (a + c) + (b + d)
• Произведение сыса на целое число: n(a + b) = na + nb, где n — целое число
• Сумма двух сысов возводится в квадрат: (a + b)^2 = a^2 + 2ab + b^2

Сысы представляют собой важный инструмент в теории чисел и имеют широкий спектр применений. Понимание этого понятия помогает математикам решать различные задачи и исследовать свойства чисел в глубину.