Что такое ребро графа в математике

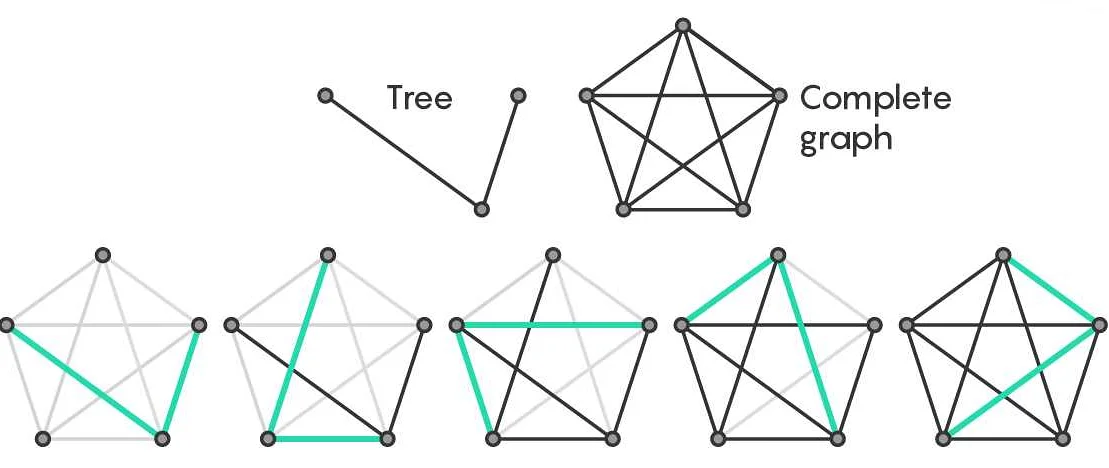
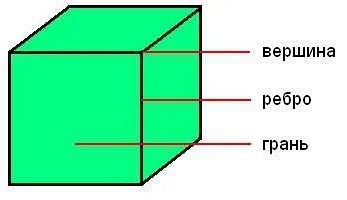
Ребро графа в математике — это связь или соединение между двумя вершинами. Оно определяет отношение или взаимодействие между этими вершинами и является основным строительным блоком графов. Ребра могут быть направленными или ненаправленными, иметь вес или не иметь. Понимание ребер графа важно для анализа и решения различных задач, связанных с моделированием и сетевыми структурами.

Ребро графа — это одно из основных понятий в теории графов, ветви математики, изучающей связности и структуру связей между объектами. Граф представляет собой набор вершин и ребер, где каждое ребро соединяет две вершины. Таким образом, ребро графа можно представить как линию, которая соединяет две точки на плоскости или в пространстве.

Ребра графа могут быть направленными или ненаправленными. В случае направленных ребер каждое ребро имеет определенное направление, то есть можно указать, какая вершина является началом ребра, а какая — его концом. В случае ненаправленных ребер направление не имеет значения, и ребра можно представить как неориентированные линии, которые связывают вершины графа.

Примеры ребер графа в различных областях знаний весьма обширны. В компьютерной графике ребра используются для визуализации связей между объектами. В транспортных сетях ребра графа представляют дороги и маршруты. В социальных сетях ребра могут представлять отношения между пользователями и их взаимодействия. В математике ребра графа активно используются для решения задач комбинаторики, теории вероятностей и других областей.

Ребро графа: определение и примеры

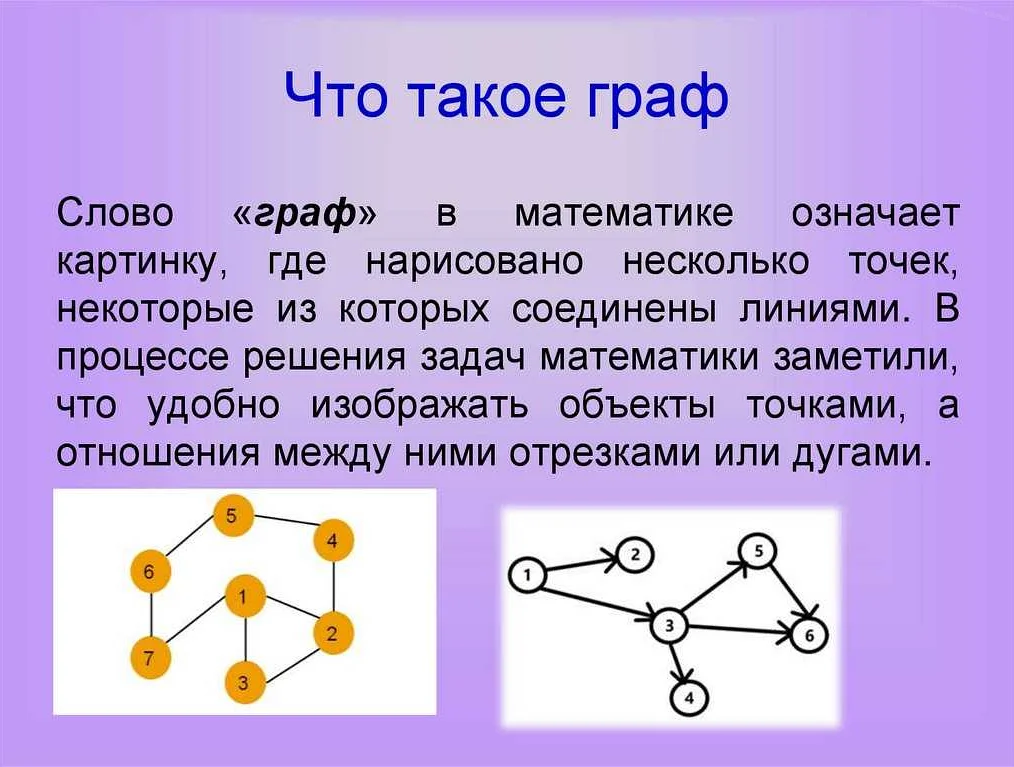
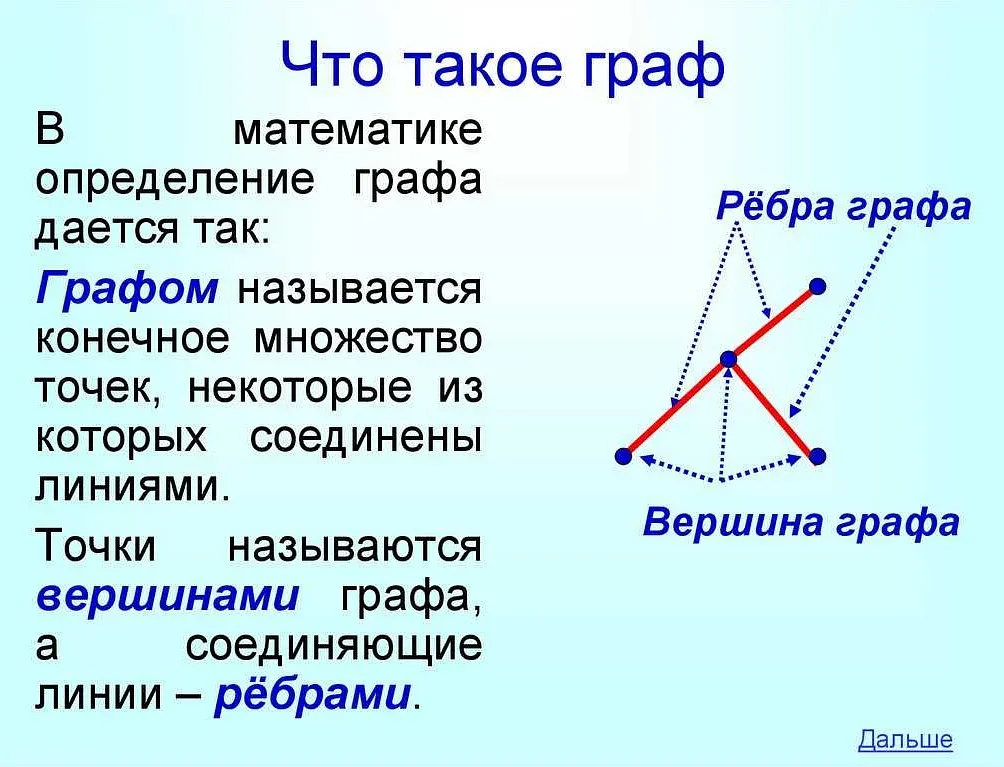
Пример 1: Рассмотрим граф дружбы между людьми. Каждый человек представляется вершиной, а дружеские связи — ребрами. Если два человека дружат друг с другом, то между их вершинами будет нарисовано ребро. Таким образом, ребра графа покажут, кто из друзей связан между собой.

Пример 2: Рассмотрим граф дорожной сети. Каждый город представляется вершиной, а дороги между городами — ребрами. Если между двумя городами есть дорога, то между соответствующими вершинами будет нарисовано ребро. Таким образом, ребра графа покажут, какие города связаны дорогами.

Из этих примеров видно, что ребра графа помогают визуализировать и анализировать различные отношения и связи между объектами. Они играют важную роль в теории графов и имеют множество применений в различных областях, таких как социология, логистика, компьютерные науки и многое другое.

Определение ребра графа

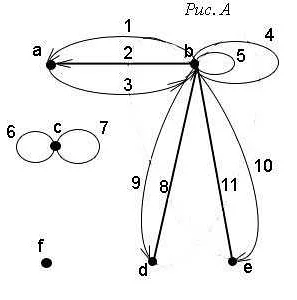
Граф представляет собой абстрактную структуру данных, состоящую из множества вершин и ребер, где каждое ребро указывает на связь между двумя вершинами.

Ребра могут быть направленными или ненаправленными. В направленном графе ребро указывает на направление связи между вершинами, тогда как в ненаправленном графе связь между вершинами является взаимной.

Ребра графа могут иметь различные атрибуты, такие как вес или стоимость, которые отражают дополнительную информацию о связи между вершинами.

Примеры ребер графа:

• В графе дорожной сети, вершины могут представлять города, а ребра — дороги, соединяющие эти города.
• В социальном графе, вершины могут представлять людей, а ребра — связи между людьми, такие как дружба или родство.
• В графе интернета, вершины могут представлять веб-страницы, а ребра — ссылки между страницами.

Ребра графа являются важным понятием в теории графов, которая находит применение в различных областях, таких как компьютерные науки, транспортная логистика, социальные сети и другие.

Ориентированное ребро графа

Ориентированные ребра используются для моделирования различных взаимодействий и отношений в графе. Они могут быть использованы для представления направления движения, потока информации, зависимостей или заказов.

Например, представим граф, который моделирует зависимость предметов в учебном плане. Каждая вершина будет представлять предмет, а ориентированное ребро будет указывать на то, что для изучения одного предмета необходимо предварительно изучить другой предмет.

В математике ориентированное ребро графа обозначается стрелкой, которая указывает направление от одной вершины к другой. Например, если есть ориентированное ребро, идущее от вершины A к вершине B, то оно будет обозначаться как (A, B).

Ориентированные ребра могут быть использованы в различных алгоритмах, таких как алгоритмы поиска пути или алгоритмы топологической сортировки. Они позволяют более точно моделировать и решать различные задачи, связанные с графами.

Неориентированное ребро графа

Неориентированные ребра играют важную роль в анализе и моделировании различных систем. Например, в социальных сетях вершины могут представлять пользователей, а неориентированные ребра могут соединять пользователей, которые являются друзьями или имеют какое-либо другое взаимодействие.

Примером неориентированного ребра может служить мост, который соединяет два берега реки. Мост не имеет начала или конца, и вы можете перейти с одного берега на другой в любом направлении. Также неориентированными ребрами могут быть дороги, которые соединяют два города, или провода, которые связывают электронные компоненты в электрической схеме.

Примеры ребер графа

Ребро графа представляет собой связь между двумя вершинами. Ниже приведены несколько примеров ребер графа:

Пример 1: Рассмотрим граф, представляющий собой дорожную сеть города. Вершины графа будут представлять различные узлы и перекрестки дорог, а ребра — сами дороги между этими узлами. Например, ребро может соединять два перекрестка и представлять собой конкретную улицу или дорогу.

Пример 2: Рассмотрим граф, представляющий собой социальную сеть. Вершины графа будут представлять пользователей социальной сети, а ребра — связи между этими пользователями. Например, ребро может соединять двух пользователей, если они являются друзьями или имеют другие виды взаимосвязи.

Пример 3: Рассмотрим граф, представляющий собой сеть компьютеров в локальной сети. Вершины графа будут представлять компьютеры, а ребра — связи между этими компьютерами, обозначающие возможность обмена данными. Например, ребро может соединять два компьютера, если они находятся в одной сети и могут обмениваться информацией.

Таким образом, ребра графа являются ключевыми элементами структуры графа, определяющими связи и взаимодействие между вершинами. Они позволяют анализировать и моделировать различные типы сетей и систем.

Ребро графа в математическом анализе

Ребра графа могут иметь различные характеристики, такие как направленность, вес или метку. Направленные ребра указывают на однонаправленную связь между вершинами, тогда как ненаправленные ребра описывают двухстороннюю связь. Вес ребра может указывать на стоимость или длину связи, а метка может представлять дополнительную информацию о ребре.

Примерами ребер графа в математическом анализе могут служить:

• Дороги между городами, где вершины представляют собой города, а ребра — дороги;
• Связи между страницами веб-сайта, где вершины — страницы, а ребра — ссылки;
• Отношения между людьми в социальных сетях, где вершины — пользователи, а ребра — связи между ними.

Ребра графа являются важным инструментом для анализа и моделирования различных систем и явлений. Они позволяют представить связи между объектами и изучать их свойства и взаимодействия.

Видео по теме:

Вопрос-ответ:

Что такое ребро графа?

Ребро графа в математике — это соединяющая линия или дуга, которая соединяет две вершины графа.

Какие свойства имеет ребро графа?

Ребро графа может быть направленным или ненаправленным. Также ребро может иметь вес, который указывает на стоимость или расстояние между двумя вершинами.

Приведите примеры ребер графа.

Примеры ребер графа могут включать дороги, которые соединяют города, ребра на поле шахматной доски или соединения между страницами веб-сайта.

Какие виды ребер графа существуют?

В графе могут быть направленные ребра, которые указывают на однонаправленную связь между вершинами, и ненаправленные ребра, которые позволяют перемещаться между вершинами в любом направлении.

Какое значение имеет вес ребра графа?

Вес ребра графа может указывать на стоимость прохождения пути между двумя вершинами, такую как расстояние или время. Вес может быть использован для определения наименьшего или наиболее оптимального пути в графе.

Что такое ребро графа?

Ребро графа — это элементарная часть графа, которая соединяет две вершины. Оно представляет собой связь или отношение между двумя вершинами графа.

Ребро графа в компьютерных науках

Ребра графа в компьютерных науках широко используются для моделирования различных систем и связей. Например, в сетях компьютеров ребра могут представлять собой физические соединения между узлами, а в графовых базах данных они могут представлять отношения между сущностями.

Ребра графа в компьютерных науках могут иметь различные атрибуты, такие как вес или стоимость. Вес ребра может использоваться для определения длины или затраты прохождения через это ребро, а стоимость может представлять собой некоторую цену или ресурс, связанный с этим ребром.

Одним из примеров использования ребер графа в компьютерных науках является алгоритм поиска кратчайшего пути. В этом случае ребра представляют собой связи между различными вершинами графа, а алгоритм используется для определения наименьшего количества ребер, необходимых для достижения одной вершины из другой.

Таким образом, ребра графа в компьютерных науках играют важную роль в решении различных задач, связанных с моделированием и анализом систем и связей. Их свойства и атрибуты могут быть использованы для определения различных характеристик и свойств графа, что позволяет эффективно решать разнообразные задачи в компьютерных науках.

Ребро графа в социальных науках

Ребра графа в социальных науках могут иметь различные характеристики и значения, в зависимости от контекста исследования. Например, в социальной сети ребро может представлять дружескую связь между двумя людьми, а в организационной структуре ребро может означать иерархическую связь между руководителем и подчиненным.

Анализ ребер графа в социальных науках позволяет исследователям понять структуру и динамику социальных сетей, идентифицировать ключевых актеров или группы, а также выявить паттерны взаимодействия и потенциальные влияния. Такой анализ может быть полезен в различных областях, включая социологию, психологию, политическую науку и маркетинг.

Примеры ребер графа в социальных науках:

1. Дружеские связи между пользователями социальной сети.
2. Связи между сотрудниками внутри организации.
3. Отношения между политическими партиями или кандидатами на выборах.
4. Связи между актерами в киноиндустрии.
5. Связи между научными статьями или авторами в академическом мире.

Изучение ребер графа в социальных науках позволяет увидеть связи и отношения, которые могут оказывать влияние на различные аспекты социальной жизни и поведения.