Что такое теория вероятности в математике

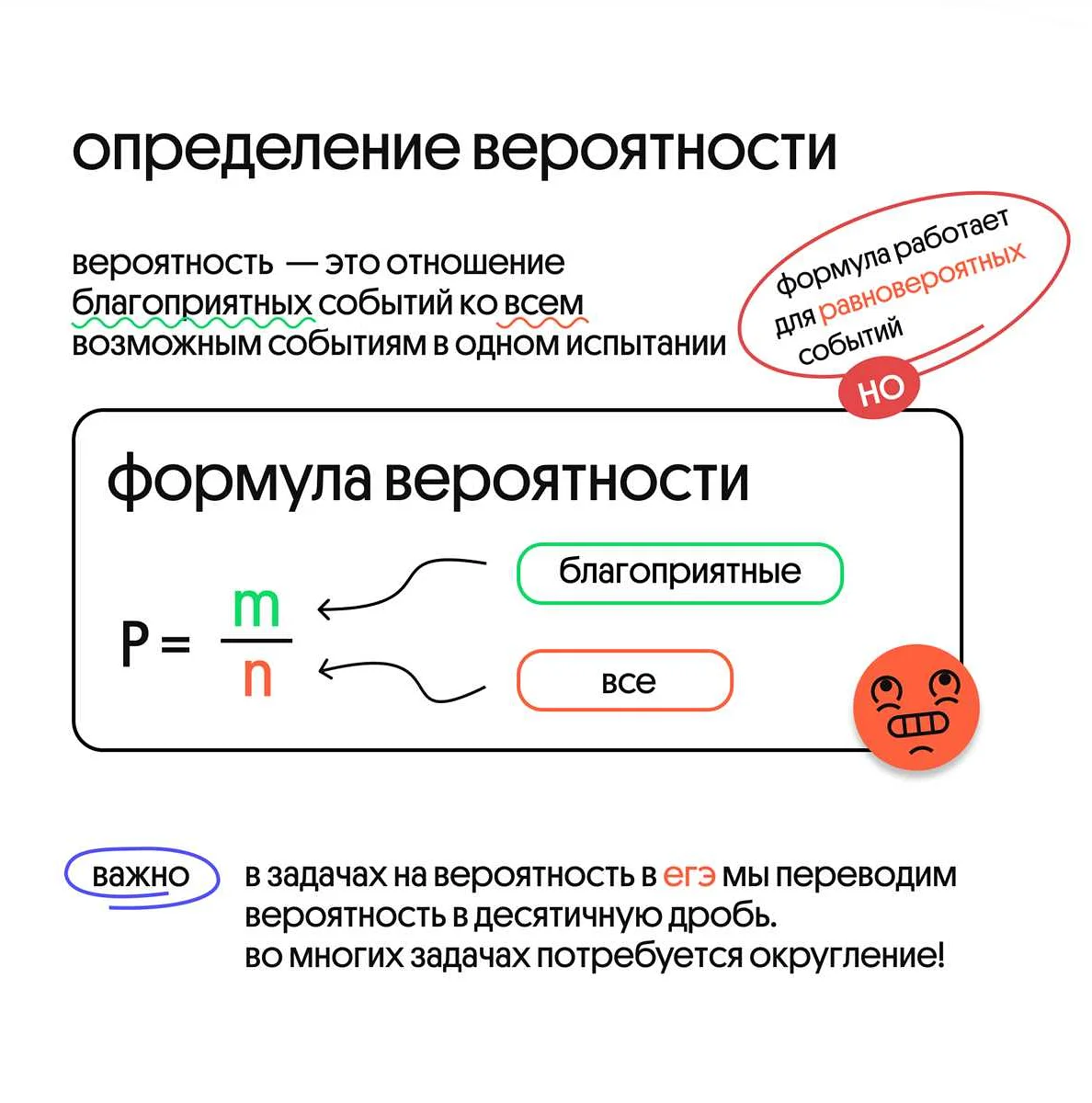
Теория вероятности — это раздел математики, который изучает случайные события и их вероятности. В данной статье рассмотрены основные понятия и принципы теории вероятности, а также примеры и приложения этой науки. Узнайте, как оценивать вероятность различных событий и использовать теорию вероятности в решении практических задач.

Теория вероятности – это раздел математики, который изучает случайные явления и вероятности их возникновения. Основная задача теории вероятности – изучить и описать вероятности различных событий и их свойства. Также она позволяет прогнозировать вероятности будущих событий на основе изученных данных.

Основные понятия теории вероятности включают в себя понятия вероятности, случайной величины, события, вероятностного пространства, статистической зависимости и независимости. Вероятность – это числовая характеристика случайного события, которая показывает, насколько оно вероятно. Случайная величина – это функция, которая сопоставляет каждому элементарному исходу некоторого случайного эксперимента числовое значение. Событие – это некоторое множество элементарных исходов, которое может произойти или не произойти.

Применение теории вероятности находится во многих областях. Например, в статистике, физике, экономике, биологии, психологии и т.д. В статистике теория вероятности используется для анализа данных и вывода статистических закономерностей. В физике она применяется при моделировании случайных процессов и описании случайных флуктуаций. В экономике теория вероятности используется для прогнозирования финансовых рынков и оценки рисков. А в биологии и психологии она помогает изучать случайные процессы в организмах и исследовать поведение людей.

Определение и история развития

Понятие вероятности и первые идеи теории вероятности возникли еще в античности. Древнегреческими философами, такими как Аристотель и Эпикур, были предложены первые основные принципы вероятности. Однако, формальное развитие теории вероятности началось только в XVII веке.

В 1654 году французский математик Блез Паскаль и его коллега Пьер де Ферма занимались изучением проблемы разделения ставок при незавершенных играх в азартные игры. Они разработали основные правила для распределения выигрыша в зависимости от вероятности наступления определенного исхода. Это и стало отправной точкой для развития теории вероятности.

В XVIII веке теория вероятности получила развитие благодаря работам Абрахама де Муавра, который стал одним из основоположников статистики и теории вероятностей. В своей работе «Расчеты по играм случая» Муавр предложил методы анализа случайных явлений и определения их вероятностей.

Основные понятия и принципы теории вероятности были формализованы в XIX веке. В 1814 году французский математик Пьер-Симон Лаплас опубликовал свою работу «Теория аналитических вероятностей», в которой он предложил математический аппарат для изучения случайных явлений. Лаплас внес значительный вклад в развитие теории вероятностей и статистики.

В XX веке теория вероятности стала широко применяться в различных областях науки и техники — от физики и экономики до биологии и информатики. С появлением компьютеров стала возможной численная обработка больших объемов данных и моделирование различных случайных процессов.

Сегодня теория вероятности является одной из основных дисциплин математики, которая находит применение во многих областях науки, техники и практических задачах. Она позволяет рассчитывать вероятности различных событий, строить статистические модели и прогнозировать возможные исходы случайных процессов.

Видео по теме:

Вероятностное пространство и элементарные события

Элементарные события — это возможные исходы некоторого случайного эксперимента, которые не могут быть разделены на более простые исходы. Например, при броске правильной монеты элементарные события могут быть «выпадение герба» и «выпадение решки».

Вероятностное пространство задается тройкой (Ω, F, P), где:

• Ω — множество всех возможных исходов случайного эксперимента;
• F — сигма-алгебра, которая содержит некоторые подмножества Ω, называемые событиями;
• P — функция вероятности, сопоставляющая каждому событию из F число от 0 до 1.

Функция вероятности P должна удовлетворять некоторым условиям. В частности, сумма вероятностей всех событий должна быть равна 1.

Вероятностное пространство позволяет формализовать и изучать случайные явления и вычислять вероятность различных событий.

Пример:

Рассмотрим эксперимент броска игральной кости. Множество возможных исходов этого эксперимента будет содержать числа от 1 до 6. Событиями могут быть, например, «выпадение четного числа» или «выпадение числа больше 4». Функция вероятности будет присваивать каждому событию вероятность, равную отношению количества благоприятных исходов к общему количеству исходов.

События и операции над ними

События можно комбинировать с помощью операций над ними. Основные операции включают:

Объединение (обозначается как A ∪ B) — это операция, при которой событие A или событие B или оба события происходят одновременно. Например, если A — выпадение орла, а B — выпадение решки, то A ∪ B — выпадение орла или решки.

Пересечение (обозначается как A ∩ B) — это операция, при которой событие A и событие B происходят одновременно. Например, если A — выпадение орла, а B — выпадение решки, то A ∩ B — невозможное событие, так как орел и решка не могут выпасть одновременно.

Дополнение (обозначается как ¬A) — это операция, при которой происходит событие, противоположное событию A. Например, если A — выпадение орла, то ¬A — выпадение решки.

Разность (обозначается как A \ B) — это операция, при которой происходит событие A, но не происходит событие B. Например, если A — выпадение орла, а B — выпадение решки, то A \ B — выпадение орла без выпадения решки.

Зная базовые операции над событиями, можно строить более сложные комбинации событий и рассчитывать их вероятности. Также операции над событиями позволяют формулировать и доказывать различные теоремы и правила в теории вероятности.

Вероятность события и ее свойства

Вероятность события обладает следующими свойствами:

1. Вероятность события всегда находится в диапазоне от 0 до 1, то есть 0 ≤ P(A) ≤ 1. Вероятность 0 означает, что событие никогда не произойдет, а вероятность 1 означает, что событие обязательно произойдет.
2. Вероятность противоположного события равна единице минус вероятность данного события. То есть P(¬A) = 1 — P(A), где ¬A — противоположное событие к A.
3. Если два события A и B несовместны (не могут произойти одновременно), то вероятность их объединения равна сумме их вероятностей. То есть P(A ∪ B) = P(A) + P(B).
4. Если событие A влечет за собой событие B, то вероятность события B не меньше вероятности события A. То есть если A → B, то P(B) ≥ P(A).
5. Если два события A и B независимы (наступление одного события не влияет на наступление другого), то вероятность их пересечения равна произведению их вероятностей. То есть P(A ∩ B) = P(A) * P(B).

Эти свойства вероятности являются основными и широко используются в применении теории вероятности для решения различных задач и моделирования случайных явлений.

Условная вероятность и независимость событий

Формула для вычисления условной вероятности:

P(A|B) = P(A и B) / P(B)

Где P(A и B) — вероятность того, что произойдут и событие A, и событие B, а P(B) — вероятность наступления события B.

Примером условной вероятности может служить следующая ситуация: из колоды в 52 карты мы выбираем одну карту. Если наш выбор падает на червовую карту, то мы хотим вычислить вероятность того, что эта карта будет дамой. Здесь A — событие «выбранная карта — дама», а B — событие «выбранная карта — червовая».

Независимость событий — это свойство двух или более событий, при котором наступление или не наступление одного из них не влияет на вероятность наступления другого. То есть события независимы, если вероятность наступления одного события не зависит от наступления или не наступления другого события.

Два события A и B называются независимыми, если выполняется следующее условие:

P(A и B) = P(A) * P(B)

Если условие P(A и B) = P(A) * P(B) выполняется, то события называются независимыми. Если же это условие не выполняется, то события являются зависимыми.

Пример независимости событий: если мы подбрасываем монету два раза, то вероятность выпадения герба на первом броске не влияет на вероятность выпадения герба на втором броске. Это значит, что события «герб на первом броске» и «герб на втором броске» являются независимыми.

Статистические законы и распределения

Теория вероятности в математике изучает случайные явления и события, и статистические законы и распределения играют важную роль в этой области. Статистические законы описывают вероятности различных исходов случайных экспериментов, а распределения показывают, как вероятность распределена между этими исходами.

Одним из наиболее известных законов вероятности является закон больших чисел. Он утверждает, что с увеличением числа испытаний среднее значение случайной величины стремится к ее математическому ожиданию. Это означает, что при повторении эксперимента много раз мы получим результат, который близок к теоретическому ожиданию.

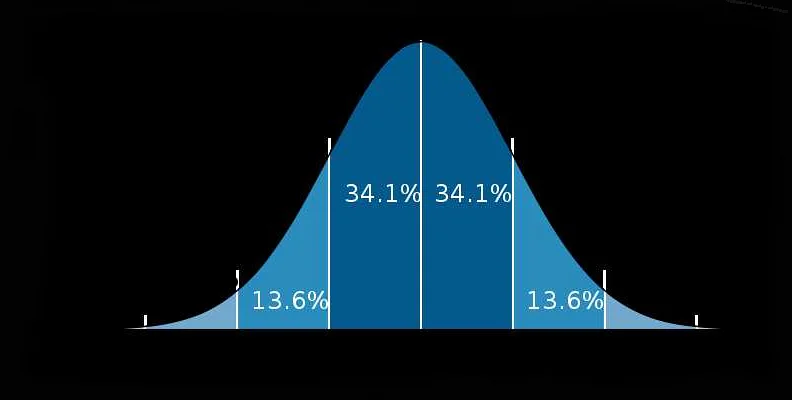
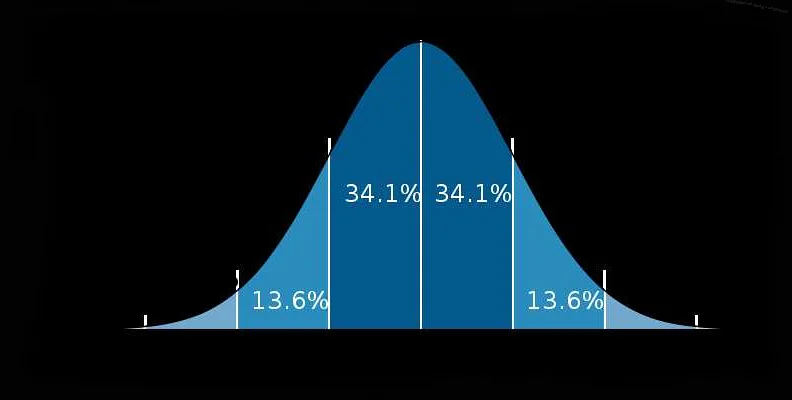
Существует также ряд распределений, которые часто используются в теории вероятности и статистике. Например, нормальное распределение часто встречается в природе и моделирует множество случайных явлений. Оно имеет симметричную форму и характеризуется своими параметрами — средним значением и стандартным отклонением.

РаспределениеОписание

Биномиальное распределение	Моделирует число успехов в серии независимых экспериментов с двумя возможными исходами.
Пуассоновское распределение	Моделирует количество редких событий, происходящих в определенном временном или пространственном интервале.
Экспоненциальное распределение	Моделирует время, прошедшее между последовательными редкими событиями.
Гамма-распределение	Моделирует время ожидания наступления заданного числа редких событий.

Статистические законы и распределения являются основой для многих статистических методов и моделей, которые используются для анализа данных и принятия решений на основе этих данных. Понимание этих законов и распределений позволяет ученым и исследователям проводить статистические исследования, прогнозировать вероятности и делать выводы на основе данных.

Применение теории вероятности в реальной жизни

Теория вероятности, разработанная в математике, имеет широкое применение в реальной жизни. Она позволяет анализировать вероятность наступления событий и принимать обоснованные решения на основе этой информации.

Одной из областей, где теория вероятности активно используется, является страхование. Страховые компании используют вероятностные модели для определения рисков и расчета страховых премий. На основе статистических данных и вероятностных расчетов, они могут предсказать вероятность наступления определенных событий, таких как автомобильная авария или возникновение пожара, и установить соответствующие страховые тарифы.

Теория вероятности также широко применяется в финансовой сфере. Финансовые аналитики используют статистические методы и модели вероятности для анализа рынка, прогнозирования цен акций и оценки рисков. Например, они могут использовать модели стохастического процесса для предсказания будущих изменений цен на акции или опционы.

В медицине теория вероятности играет важную роль в диагностике и прогнозировании заболеваний. Врачи и исследователи могут использовать статистические методы и анализ данных для определения вероятности развития определенного заболевания или эффективности лечения. Это помогает им принимать обоснованные решения о диагностике и лечении пациентов.

Теория вероятности также находит применение в инженерии и производстве. Инженеры используют вероятностные методы для анализа надежности и безопасности систем и процессов. Например, они могут рассчитывать вероятность отказа определенной детали или предсказывать время безотказной работы системы.

В заключение, теория вероятности играет важную роль в различных сферах жизни, помогая прогнозировать и анализировать вероятность наступления событий. Она позволяет принимать обоснованные решения, основанные на вероятностных расчетах и статистических данных. Без нее многие области науки и промышленности были бы значительно усложнены.

Основные области применения теории вероятности

1. Математическая статистика	Теория вероятности является основой для математической статистики. Она позволяет описывать и анализировать случайные явления, проводить статистические исследования на основе собранных данных, делать выводы и прогнозы.
2. Теория информации	Теория вероятности играет ключевую роль в теории информации. Она позволяет измерять количество информации, определять вероятность передачи или хранения информации, а также разрабатывать методы сжатия данных.
3. Физика	В физике теория вероятности применяется для описания случайных процессов и явлений, таких как распад атомных ядер, движение частиц, квантовая механика и т.д. Она позволяет предсказывать вероятность наступления определенных событий и проводить статистические измерения.
4. Финансовая математика	Теория вероятности широко используется в финансовой математике для моделирования и анализа финансовых рынков, оценки рисков и прогнозирования ценовых движений. Она позволяет определить вероятность получения прибыли или убытка при различных инвестиционных стратегиях.
5. Искусственный интеллект	Теория вероятности имеет применение в области искусственного интеллекта. Она используется для разработки алгоритмов машинного обучения, распознавания образов, обработки естественного языка и других задач, связанных с анализом больших объемов данных.

Это лишь небольшой перечень областей, в которых применяется теория вероятности. Ее применение распространено практически во всех научных и практических дисциплинах, где важно учитывать случайные факторы и неопределенность.

Вопрос-ответ:

Сколько времени занимает изучение теории вероятности?

Время, необходимое для изучения теории вероятности, может варьироваться в зависимости от уровня подготовки и интенсивности занятий. Если вы уже знакомы с математикой и имеете базовые знания о вероятности, то освоение основных понятий может занять несколько недель. Однако для полного понимания и углубленного изучения теории вероятности может потребоваться несколько месяцев или даже лет.

Каковы основные понятия теории вероятности?

Основные понятия теории вероятности включают вероятность, случайную величину, событие, пространство элементарных исходов, условную вероятность, независимость событий и т. д. Вероятность — это числовая характеристика того, насколько вероятно наступление данного события. Случайная величина — это функция, которая присваивает числовое значение каждому элементарному исходу в некотором эксперименте. Событие — это некоторое множество элементарных исходов, которые удовлетворяют определенному условию. Пространство элементарных исходов — это множество всех возможных исходов эксперимента. Условная вероятность — это вероятность наступления события при условии, что произошло другое событие. Независимость событий означает, что наступление одного события не влияет на вероятность наступления другого события.

В каких областях науки применяется теория вероятности?

Теория вероятности находит применение в различных областях науки и жизни. Например, в экономике она используется для моделирования финансовых рынков и оценки рисков. В физике вероятностные методы применяются при изучении квантовой механики и статистической физики. В биологии теория вероятности помогает анализировать мутации, эволюцию и генетические процессы. В компьютерных науках вероятностные методы используются для разработки алгоритмов искусственного интеллекта и обработки данных. Кроме того, теория вероятности применяется в статистике, игровой теории, теории управления и многих других областях.

Какие основные понятия входят в теорию вероятности?

Основные понятия в теории вероятности включают вероятностное пространство, случайные события, вероятность события, условная вероятность, независимость событий и математическое ожидание.

Какие практические применения имеет теория вероятности?

Теория вероятности имеет множество практических применений. Она используется в статистике для анализа данных, в финансовой математике для моделирования рисков, в технической диагностике для определения вероятности отказа оборудования, в машинном обучении для построения алгоритмов, и во многих других областях.

Какие свойства имеет вероятность события?

Вероятность события является числом от 0 до 1 и обладает несколькими свойствами. Вероятность объединения двух несовместных событий равна сумме их вероятностей. Вероятность противоположного события равна единице минус вероятность исходного события. Вероятность пустого события равна нулю. И вероятность выполнения хотя бы одного из нескольких независимых событий равна сумме их вероятностей минус вероятность их пересечения.