Что называют математическим ожиданием нсв

Математическое ожидание случайной величины (НСВ) – это среднее значение, которое можно ожидать в результате проведения эксперимента или случайного события. Узнайте, как вычислять математическое ожидание и зачем оно используется в статистике и вероятностных расчетах.

Математическое ожидание – один из фундаментальных понятий теории вероятностей, которое применяется при анализе случайных явлений. Оно позволяет оценить среднее значение случайной величины, то есть предсказать, каким будет ее среднее значение в долгосрочной перспективе. В контексте непрерывных случайных величин математическое ожидание определяется как интеграл от произведения значения случайной величины на ее плотность распределения.

Математическое ожидание непрерывной случайной величины имеет несколько интерпретаций. Во-первых, оно представляет собой среднюю оценку значения случайной величины в условиях большого числа испытаний. Во-вторых, математическое ожидание может рассматриваться как центр масс распределения случайной величины. В-третьих, оно может интерпретироваться как средневзвешенное значение, где весами являются вероятности, с которыми принимаются разные значения случайной величины.

Примером непрерывной случайной величины может служить время ожидания на остановке общественного транспорта. Предположим, что время ожидания имеет равномерное распределение на интервале от 0 до 10 минут. Тогда математическое ожидание можно рассчитать как среднее значение на этом интервале, то есть 5 минут. Это означает, что в среднем пассажир будет ждать автобус 5 минут.

Что такое математическое ожидание непрерывной случайной величины?

Математическое ожидание непрерывной случайной величины вычисляется по следующей формуле:

Где f(x) — плотность вероятности непрерывной случайной величины, а x — значение, для которого вычисляется математическое ожидание.

Например, для непрерывного равномерного распределения на отрезке [a, b], математическое ожидание вычисляется по формуле:

Где a и b — границы отрезка распределения.

Математическое ожидание непрерывной случайной величины является важной характеристикой, которая позволяет оценить среднее значение и предсказать поведение данной случайной величины в долгосрочной перспективе.

Определение математического ожидания

Формально, математическое ожидание для непрерывной случайной величины X может быть определено следующим образом:

ОпределениеФормула

Для дискретной случайной величины	E[X] = ∑ xi * pi
Для непрерывной случайной величины	E[X] = ∫ x * f(x) dx

В первом случае, где X — дискретная случайная величина, xi — возможное значение случайной величины, а pi — вероятность этого значения.

Во втором случае, где X — непрерывная случайная величина, f(x) — плотность вероятности случайной величины.

Математическое ожидание позволяет оценить среднее значение случайной величины и является одной из основных характеристик случайного процесса. Оно имеет важное теоретическое и практическое значение во многих областях науки, экономики и инженерии.

Основные свойства математического ожидания

Математическое ожидание обладает рядом свойств, которые делают его удобным инструментом для анализа случайных величин:

СвойствоФормулировка

Линейность	Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Аддитивность	Математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.
Масштабирование	Математическое ожидание произведения случайной величины на константу равно произведению этой константы на математическое ожидание случайной величины.
Нормировка	Математическое ожидание случайной величины, деленное на ее стандартное отклонение, равно 1.

Эти свойства позволяют упростить вычисление математического ожидания и использовать его для анализа различных случайных величин. Они являются основой для дальнейшего изучения и применения теории вероятностей и статистики.

Пример 1: Математическое ожидание равномерно распределенной случайной величины

Рассмотрим случайную величину X, которая равномерно распределена на отрезке [a, b]. Математическое ожидание такой случайной величины можно вычислить по формуле:

Математическое ожидание = (a + b) / 2

Например, пусть случайная величина X равномерно распределена на отрезке [0, 10]. Тогда математическое ожидание этой случайной величины будет равно:

Математическое ожидание = (0 + 10) / 2 = 5

Таким образом, в данном примере математическое ожидание равномерно распределенной случайной величины на отрезке [0, 10] равно 5.

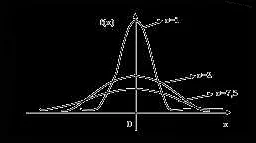
Пример 2: Математическое ожидание нормально распределенной случайной величины

Предположим, что у нас есть нормально распределенная случайная величина X с параметрами математического ожидания (средним значением) μ и дисперсией σ^2. Нормальное распределение часто используется в статистике для моделирования случайных величин.

Математическое ожидание нормально распределенной случайной величины можно вычислить по формуле:

E(X) = μ

То есть, математическое ожидание нормально распределенной случайной величины равно ее среднему значению, которое задается параметром μ.

Например, предположим, что у нас есть нормально распределенная случайная величина X, которая представляет собой рост взрослого населения. Пусть средний рост равен 170 см, а дисперсия равна 25 см^2. Тогда математическое ожидание этой случайной величины будет равно 170 см.

Математическое ожидание нормально распределенной случайной величины позволяет нам оценить среднее значение этой случайной величины и использовать его в дальнейших расчетах и анализе данных.

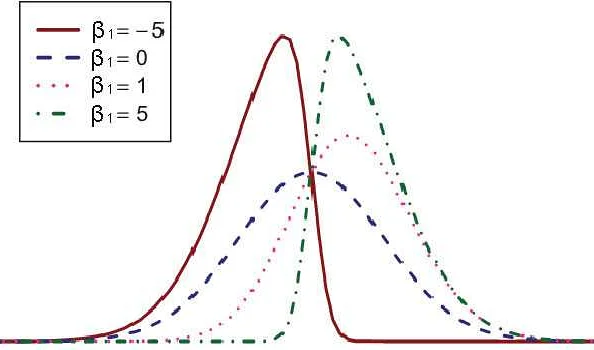
Пример 3: Математическое ожидание экспоненциально распределенной случайной величины

Рассмотрим случайную величину, распределенную по экспоненциальному закону. Экспоненциальное распределение описывает время между последовательными событиями в пуассоновском процессе.

Пусть случайная величина X имеет экспоненциальное распределение с параметром λ. Вероятность того, что X принимает значение x, можно выразить функцией плотности вероятности:

f(x) = λ * exp(-λx)

Математическое ожидание (математическое среднее) для экспоненциально распределенной случайной величины можно вычислить по формуле:

E(X) = 1/λ

То есть, математическое ожидание равно обратной величине параметра λ.

Например, пусть случайная величина X описывает время между приходом двух последовательных автобусов на остановку. Предположим, что среднее время между приходами автобусов составляет 10 минут. Тогда параметр λ будет равен 1/10, и математическое ожидание будет равно 10 минут.

Математическое ожидание позволяет оценить среднее значение случайной величины и предсказать ее поведение в среднем. В данном примере, математическое ожидание показывает, что в среднем время между приходами автобусов будет составлять 10 минут.

Значение математического ожидания в статистике и экономике

В экономике математическое ожидание позволяет оценить средний уровень доходов или расходов, что является важным при принятии решений в сфере экономики и финансов. Например, математическое ожидание может быть использовано для прогнозирования прибыли или убытков от определенной инвестиции.

Для расчета математического ожидания в статистике и экономике используется формула:

E(X) = ∫x * f(x) dx

где E(X) — математическое ожидание случайной величины X, x — значение случайной величины, f(x) — функция плотности вероятности случайной величины.

Таким образом, математическое ожидание позволяет получить числовую характеристику случайной величины, на основе которой можно делать выводы о ее поведении и прогнозировать будущие значения.

Вопрос-ответ:

Что такое математическое ожидание непрерывной случайной величины?

Математическое ожидание непрерывной случайной величины — это среднее значение этой случайной величины, которое можно ожидать в результате многократного повторения эксперимента. Оно вычисляется путем интегрирования произведения значения случайной величины на ее плотность вероятности по всем возможным значениям.

Как вычислить математическое ожидание непрерывной случайной величины?

Для вычисления математического ожидания непрерывной случайной величины нужно умножить каждое значение случайной величины на его вероятность и просуммировать эти произведения по всем возможным значениям. В случае непрерывной случайной величины, эта сумма заменяется на интеграл, где вместо суммирования используется интегрирование по всем возможным значениям.

Какие примеры можно привести для наглядного представления математического ожидания непрерывной случайной величины?

Примерами математического ожидания непрерывной случайной величины могут быть: вычисление среднего значения длительности звонков в минутах, среднего значения возраста людей в определенной группе, среднего значения дохода населения в определенном регионе.

Как математическое ожидание непрерывной случайной величины помогает в решении задач?

Математическое ожидание непрерывной случайной величины помогает в решении задач, связанных с описанием и предсказанием случайных явлений. Например, оно может использоваться для вычисления среднего значения прибыли от продажи товара, среднего значения времени ожидания на кассе в супермаркете, среднего значения скорости движения автомобилей на дороге.

Видео по теме: