Топология в математике: основные понятия и примеры

Топология — это раздел математики, изучающий свойства геометрических фигур и их изменения без учета размера и формы. В статье вы узнаете, что такое топологические пространства, открытые и замкнутые множества, связность и компактность, а также примеры применения топологии в других областях науки.

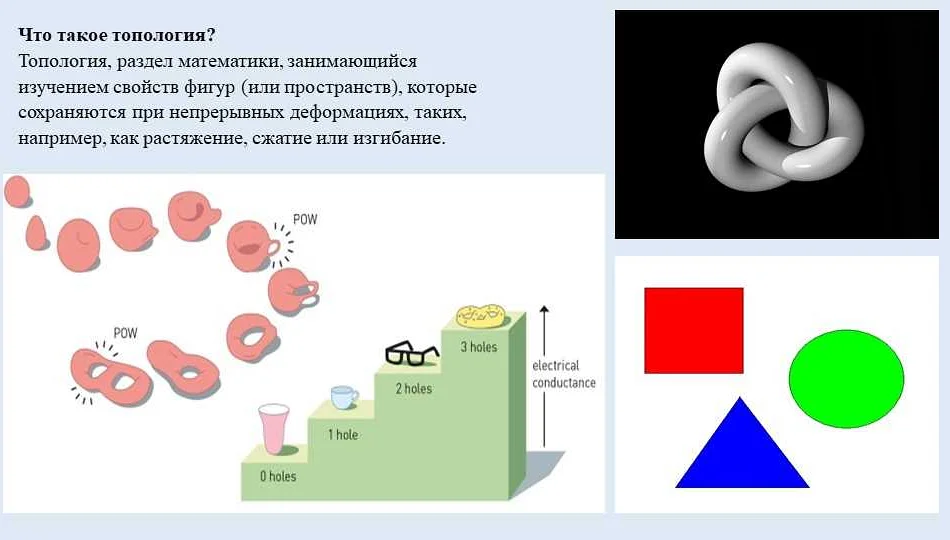
Топология — это раздел математики, изучающий свойства и отношения между пространствами, которые сохраняются при непрерывном деформировании. Другими словами, топология рассматривает геометрические объекты, которые можно размещать и преобразовывать без изменения их основных свойств.

Основные понятия топологии включают в себя топологические пространства, связность, компактность и сходимость. Топологические пространства — это множества, для которых задана топология, то есть совокупность открытых и замкнутых множеств, удовлетворяющих некоторым условиям.

Связность относится к тому, насколько близко связаны два или более множества в топологическом пространстве. Компактность — это свойство, при котором любое открытое покрытие множества содержит конечное подпокрытие. Сходимость в топологии — это понятие, которое описывает, как близки могут быть между собой различные точки в топологическом пространстве.

Примеры топологических пространств включают в себя точки на плоскости, замкнутые линии и поверхности. Топология играет важную роль в различных областях математики, таких как алгебраическая геометрия, теория вероятностей и дифференциальные уравнения.

Топология в математике: основы и применение

Топология — это одна из важнейших областей математики, занимающаяся исследованием свойств геометрических объектов, не меняющихся при непрерывных преобразованиях.

Основными понятиями топологии являются топологическое пространство, открытое и замкнутое множества, связность, компактность и метрическое пространство.

Применение топологии находится во многих областях, включая анализ данных, физику, географию, теорию графов, теорию алгоритмов и многие другие. Например, топологический анализ данных используется для выявления структурных особенностей в сложных данных, таких как многомерные массивы, графы и т.д.

Топология также широко используется в теоретической физике, особенно в теории струн, где топологические дефекты могут быть обнаружены в пространстве-времени.

Таким образом, топология является важным инструментом для изучения структуры и свойств геометрических объектов в математике, науке и инженерии.

Что такое топология в математике и зачем она нужна?

Топология — это раздел математики, изучающий свойства геометрических фигур, которые не изменятся при небольших деформациях этих фигур. Топология занимается абстрактными объектами, такими как множества и их свойствами, в том числе отношением близости, но не вдаваясь в детали их конкретного геометрического вида.

Топология находит применение в различных областях математики, физики, химии и экономики. Например, в геометрической топологии изучаются свойства многомерных фигур, в теории множеств и теории меры — свойства произвольных множеств, в теории графов — свойства связных графов. Топология также позволяет формализовать и решать различные задачи в теории вероятностей, в теории управления и даже в компьютерных науках.

Одной из главных целей топологии является классификация объектов по их топологическим свойствам. Например, два геометрически различных объекта могут быть классифицированы как «одинаковые» по своей топологии, если они обладают одинаковым набором топологических свойств. Это позволяет сводить изучение различных геометрических объектов к изучению их общих топологических свойств, что значительно облегчает и ускоряет работу в различных областях науки и техники.

Таким образом, топология играет важную роль в науке, позволяя изучать объекты на более высоком уровне абстракции и сводить изучение множества геометрических объектов к изучению их общих топологических свойств.

Основные понятия топологии: связность, компактность, открытые и замкнутые множества

Топология – это раздел математики, изучающий свойства пространств и их трансформаций. Одним из ключевых понятий топологии является понятие топологического пространства, которое состоит из множества точек и семейства подмножеств, называемых открытыми множествами.

Открытые множества в топологическом пространстве определяются таким образом, что для каждой точки этого множества можно найти ее окрестность, целиком содержащуюся в этом множестве. Замкнутые множества, наоборот, наиболее широко определяются как дополнения открытых множеств – они содержат все свои предельные точки.

Связность в топологии описывает, как множество состоит из единственного связного куска. Если множество не связно, то можно выделить несколько связных компонент, таких что внутри каждой из них не проходит никаких недопустимых разрывов.

Компактность – это свойство множества, которое позволяет найти конечное покрытие открытыми множествами, полностью покрывающее данное множество. Более формально, множество компактно, если из любого его открытого покрытия можно выбрать конечное подпокрытие.

Пространства и отображения в топологии: метрические, топологические и гомеоморфные

Топология изучает свойства пространств, которые сохраняются при непрерывном деформировании. Исследования в топологии связаны с объектами, у которых нет метрики, это значит, что не существует расстояния между элементами пространства.

В метрических пространствах используется метрика, которая определяет расстояние между элементами. Метрическая топология основывается на понятии расстояния и метрики, которая задает его. Открытые и замкнутые множества в метрическом пространстве обычно определяются исходя из метрики.

Топологические пространства определяются путем указания открытых множеств и изучаются без использования метрики. Тонкие свойства топологии не зависят от метрики и продолжают справедливость даже для пространств, где расстояние отсутствует.

Гомеоморфные отображения являются важным понятием в топологии. Две топологические структуры называются гомеоморфными, если существует биективное непрерывное отображение между ними и у обратного отображения есть те же свойства. Это значит, что они существенно «одинаковы» и могут быть преобразованы друг в друга непрерывным образом, сохраняя топологические свойства.

В заключении следует отметить, что понимание пространств и отображений в топологии имеет важное значение в различных областях математики и физики, а также при решении задач в компьютерных науках и теории информации.

Сфера и тор: примеры топологических пространств

Сфера и тор — это два известных примера топологических пространств. Топология изучает свойства, которые сохраняются при непрерывных преобразованиях. Из этого следует, что топология, в отличие от геометрии, не учитывает расстояния и размеры объектов.

Сфера — это знакомое всем геометрическое тело, ограниченное поверхностью с равномерной кривизной. Топологически, сфера является пространством, состоящим из одного связного компонента и одной дыры. Это означает, что если мы вырежем точку на сфере, то она кроме этой точки не может быть разорвана на две отдельные части.

Тор — это топологическое пространство, которое можно получить путем склеивания противоположных сторон квадрата. Тор имеет две дыры и является примером пространства с двумя связными компонентами.

Сфера и тор являются простыми и понятными примерами топологических пространств, но топологическая теория изучает и более сложные и абстрактные конструкции. Топология имеет множество приложений в науке и технике и используется, например, в теории управления, при моделировании структуры белков, и в решении задач современной математики.

Свойства топологических пространств: хаусдорфовость и нормальность

Одним из основных свойств топологических пространств является хаусдорфовость. Пространство называется хаусдорфовым, если для любых двух точек этого пространства можно найти окрестности, которые не пересекаются. Другими словами, хаусдорфово пространство достаточно «разреженное», что позволяет удобно работать с ним в теории и на практике.

Еще одним важным свойством топологических пространств является нормальность. Пространство называется нормальным, если любые два непересекающихся замкнутых множества в нем можно разделить окрестностями. То есть, если области в пространстве достаточно «выделены» друг от друга, что позволяет проводить в них независимые исследования.

Хаусдорфовость и нормальность являются важными свойствами топологических пространств и широко используются в математике и на практике. Часто, для удобства работы, именно хаусдорфовые и нормальные пространства рассматриваются вместо более общих.

Схемы баз топологии: определение и примеры

Схема базы топологии — это семейство подмножеств топологического пространства, которое удовлетворяет определенным условиям. Такие схемы представляют собой важный инструмент в топологии, поскольку позволяют задавать топологические пространства без необходимости задания всех их подмножеств.

Для того, чтобы схема базы была допустимой, необходимо, чтобы она удовлетворяла двум условиям. Во-первых, каждая точка пространства должна содержаться хотя бы в одном элементе схемы базы. Во-вторых, пересечение любых двух элементов схемы базы должно быть открытым множеством в пространстве.

Примером схемы базы может служить набор окрестностей точки в метрическом пространстве. Для любой точки существует окрестность с радиусом, например, 1, 0.5, 0.1 и т.д. Если выбрать множество всех таких окрестностей для каждой точки, получится схема базы. Эта схема базы определяет топологию, которая соответствует стандартной топологии на метрическом пространстве.

Еще одним примером может служить схема базы открытых множеств, ограниченных по размеру. Например, можно рассмотреть семейство открытых шаров в трехмерном евклидовом пространстве, радиусы которых не превышают некоторое фиксированное значение.

Различные виды топологий: дискретная, индуцированная, произведение и слабая топология

Дискретная топология: в этом виде топологии все подмножества множества являются открытыми множествами. Другими словами, каждая точка множества является открытым подмножеством.

Индуцированная топология: создается только из открытых подмножеств множества. Например, если у нас есть множество X со своей топологией, то подмножество Y является открытым в индуцированной топологии, если существует открытое подмножество U множества X такое, что U ∩ Y = Y.

Произведение топологий: создается из двух или более топологий. Этот вид топологии наиболее часто используется в топологии и многомерной геометрии. Например, если у нас есть множества X и Y, то их произведение X × Y имеет топологию, где открытое подмножество является объединением подмножеств вида U × V, где U открытое подмножество X, V открытое подмножество Y.

Слабая топология: обычно связана с теорией функционального анализа. Она определяется как наибуертая топология, в которой линейный функционал является непрерывным. В этой связи важно также отметить, что слабая топология образована непрерывными линейными функционалами и она слабее чем топология порождаемая метрикой.

• Дискретная топология: все подмножества являются открытыми;
• Индуцированная топология: строится из открытых множеств;
• Произведение топологий: создается из двух или более топологий;
• Слабая топология: определяется как наибуертая топология, в которой линейный функционал является непрерывным.

Связность топологических пространств: определение и свойства

Связность топологических пространств — это свойство, определяющее, насколько близко друг к другу расположены его точки. Если все точки tопологического пространства можно связать непрерывной кривой, то это пространство связное, иначе нет.

Если топологическое пространство распадается на две несвязных частей, то оно называется несвязным.

Путь в топологическом пространстве — это непрерывная функция из [0,1] в этом пространстве. Если для любых двух точек топологического пространства существует путь, связывающий их, то это пространство называется путь-связным.

Очевидно, что связные пространства всегда путь-связны, но не обязательно наоборот.

Компонентами связности называются максимальные связные подмножества топологического пространства. Каждое множество, не принадлежащее ни одной компоненте связности, несвязно.

Таким образом, связность топологических пространств — это важное понятие теории топологии, позволяющее описать структуру этих пространств и определить их свойства.

Компактность топологических пространств: определение и свойства

Компактность топологического пространства является одним из основных понятий топологии и связана с его свойствами и структурой. Топологическое пространство называется компактным, если из любого открытого покрытия данного пространства можно выбрать конечное подпокрытие.

Другими словами, компактное топологическое пространство является чрезвычайно плотным, что делает его особенно полезным для многих математических приложений. Например, компактные топологические пространства используются в теории дифференциальных уравнений, анализе функций и алгебре, а также в физике и инженерии.

Основные свойства компактных топологических пространств состоят в том, что они являются замкнутыми и ограниченными. Это позволяет использовать их для построения различных математических объектов и решения различных задач, включая задачи оптимизации и определение крайних точек функций.

Знание компактности топологических пространств является важным для понимания многих других концепций топологии и математики в целом, поэтому оно является неотъемлемой частью математического образования.

Видео по теме:

Вопрос-ответ:

Что такое топология в математике?

Топология — это раздел математики, изучающий свойства геометрических объектов, которые не изменятся при непрерывном деформировании их без резких пересечений и прерываний. Кратко говоря, это наука о форме и структуре объектов.

Какие основные понятия используются в топологии?

Основные понятия в топологии — это пространство, открытые и замкнутые множества, непрерывность, компактность, связность, гомеоморфность. Все эти понятия позволяют описать различные свойства и структуры в топологических пространствах.

Какие вещественные примеры можно привести для понимания топологии?

В топологии существует множество примеров, которые можно найти в повседневной жизни. Например, открытый шар является открытым множеством, а замкнутый шар — замкнутым множеством. Непрерывная деформация кольца в точки позволяет понять понятие гомеоморфизма. Также топология находит применение в картографии, географии, биологии и т.д.

Чем открытое множество отличается от замкнутого множества?

Открытое множество — это множество, для которого каждая точка внутри множества имеет окрестность, целиком содержащуюся в этом множестве. Замкнутое множество — это множество, содержащее все свои предельные точки. Иными словами, для замкнутого множества предельные точки также принадлежат этому множеству.

Что такое непрерывность в топологии?

Непрерывность — это свойство отображения, которое сохраняет топологическую структуру. То есть, если имеются два топологические пространства и отображение между ними, то это отображение является непрерывным, если прообразы открытых множеств входного пространства отображаются в открытые множества выходного пространства.

Что такое связность в топологии?

Связность — это свойство топологических пространств, которое описывает их единственность и целостность. Топологическое пространство называется связным, если оно не может быть представлено в виде объединения двух открытых непустых множеств, которые не пересекаются. Иными словами, связное топологическое пространство не может быть разделено на несколько непересекающихся частей.

Как применяется топология в математических исследованиях?

Топология имеет широкое применение в математических исследованиях. Например, она используется в анализе данных, компьютерной графике, статистической физике, теории множеств, линейной алгебре и других областях математики. Также топология играет важную роль в фундаментальных исследованиях, например, в теории струн, математической физике и других областях науки.

Использование топологии в геометрии и физике: примеры и приложения

Топология находит свое применение в различных областях науки и техники. Одним из примеров использования топологии в геометрии является определение связности графов. Также топология находит применение в изучении свойств поверхностей и пространств.

В физике топология играет важную роль при исследовании свойств материалов. С помощью топологических инвариантов можно изучать свойства материалов при различных условиях и изменениях параметров.

Одним из ярких примеров применения топологии в физике является явление квантового голографического эффекта. Этот эффект объясняется топологическими свойствами пространства и имеет важное значение в современной квантовой физике.

Также топология находит применение в изучении свойств кристаллов и материалов с неупорядоченной структурой. С помощью топологических методов можно определить различные фазы материалов и изучить их свойства при различных условиях и изменениях параметров.

В целом, топология играет важную роль в научных и технических исследованиях, позволяя изучать свойства объектов и материалов при различных условиях и изменениях параметров.

Перспективы развития топологии в математике и смежных областях науки.

Топология – это важнейшая область математики, которая имеет широкое применение в различных областях науки и техники, таких как физика, химия, компьютерные науки, инженерия и другие.

Одним из важнейших направлений развития топологии является теория узлов. Эта дисциплина исследует замкнутые кривые в 3-мерном пространстве и связанные с ними вопросы. Эта область находится на стыке топологии и математической физики и находит широкое применение, например, в изучении структуры ДНК.

Еще одним важным направлением является топологическая квантовая фазовая теория. Она изучает квантовые явления с помощью топологических методов и может использоваться в будущем для создания новых материалов и устройств.

Также различные задачи из информатики и компьютерных наук, такие как оптимизация маршрутов и проектирование сетей, могут быть решены с помощью топологии.

В целом, топология как область науки не перестает развиваться и находить новые области применения. Ее перспективы развития включают создание новых методов и идей для решения сложных проблем, а также расширение сферы ее применения в различных научных областях.