Что такое трехзначное число в математике

Трехзначное число в математике — это число, состоящее из трех цифр, которые могут быть любыми от 0 до 9. Трехзначные числа играют важную роль в арифметике, алгебре и других разделах математики. Узнайте больше о свойствах и использовании трехзначных чисел в математике.

Трехзначное число — это число, состоящее из трех цифр. Оно может принимать значения от 100 до 999 включительно. В математике трехзначные числа играют важную роль при решении задач и вычислении различных величин.

Каждая цифра в трехзначном числе имеет свое место и значение. Например, в числе 356 первая цифра 3 представляет сотни, вторая цифра 5 — десятки, а третья цифра 6 — единицы. Это позволяет нам определить вес каждой позиции и выполнять различные операции с числами, такие как сложение, вычитание, умножение и деление.

Примеры трехзначных чисел:

1) 123 — трехзначное число, где 1 — сотни, 2 — десятки, 3 — единицы.

2) 789 — также трехзначное число, где 7 — сотни, 8 — десятки, 9 — единицы.

3) 502 — трехзначное число, где 5 — сотни, 0 — десятки, 2 — единицы.

Трехзначные числа широко используются в различных сферах, таких как физика, экономика, программирование и т.д. Изучение и понимание их структуры и свойств поможет вам лучше понять и применять математические концепции в практических задачах и решениях.

Определение трехзначного числа

Трехзначные числа могут принимать значения от -999 до -100 и от 100 до 999 включительно.

Примеры трехзначных чисел:

ЧислоОписание

123	Положительное трехзначное число
-456	Отрицательное трехзначное число
789	Положительное трехзначное число
-321	Отрицательное трехзначное число

Трехзначные числа используются в различных математических операциях и задачах, а также в программировании и науке.

Конструкция трехзначного числа

ABС

Где A, B и C — цифры, принимающие значения от 0 до 9. Цифра A обозначает значение сотен, цифра B — значение десятков, а цифра C — значение единиц.

Например, число 356 является трехзначным числом. В этом случае A=3, B=5 и C=6.

Трехзначные числа могут принимать любые значения от 100 до 999. Зная конструкцию трехзначного числа, можно проводить различные операции с этими числами, такие как сложение, вычитание, умножение и деление.

Трехзначные числа широко используются в математике и других областях науки. Они могут быть использованы для представления количества предметов, измерения времени, представления координат и т.д.

Знание конструкции трехзначного числа поможет вам лучше понять и использовать математические операции и концепции в своих учебных и повседневных задачах.

Примеры трехзначных чисел

100, 101, 102, 103, 104, 105, 106, 107, 108, 109,

110, 111, 112, 113, 114, 115, 116, 117, 118, 119,

120, 121, 122, 123, 124, 125, 126, 127, 128, 129,

и так далее, до 999.

Трехзначное число в позиционной системе счисления

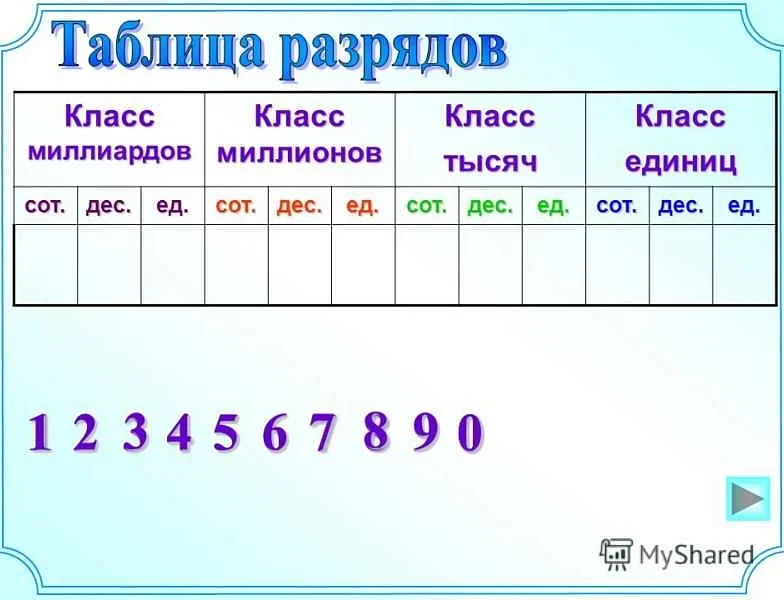
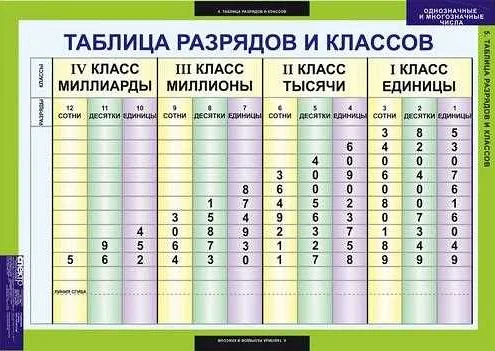
Трехзначное число представляет собой число, состоящее из трех цифр, которые находятся в определенных позициях относительно друг друга. В позиционной системе счисления каждая позиция имеет свою весовую степень, которая определяет значение цифры. Позиция самой левой цифры имеет весовую степень, равную 100 (десять в кубе), средней цифры — 10 (десять в первой степени), а самой правой цифры — 1 (десять в нулевой степени).

Примером трехзначного числа в позиционной системе счисления может быть число 247. В этом числе цифра 2 находится в позиции с весовой степенью 100, цифра 4 — в позиции с весовой степенью 10 и цифра 7 — в позиции с весовой степенью 1. При расчете значения числа учитывается вес каждой позиции: 2 * 100 + 4 * 10 + 7 * 1 = 200 + 40 + 7 = 247.

Трехзначные числа находят широкое применение в различных областях, таких как физика, экономика, информатика и других. Они позволяют удобно и компактно представлять большие числовые значения и оперировать ими в рамках позиционной системы счисления.

Трехзначное число в арифметических операциях

В арифметических операциях трехзначные числа можно складывать, вычитать, умножать и делить.

При сложении трехзначных чисел, слагаемые должны быть выровнены по разрядам (сотни, десятки, единицы) и складываться последовательно, начиная с единиц. Например:

• 123 + 456 = 579
• 789 + 321 = 1110

При вычитании трехзначных чисел, вычитаемое также должно быть выровнено по разрядам и вычитаться последовательно, начиная с единиц. Например:

• 987 — 654 = 333
• 543 — 210 = 333

При умножении трехзначного числа на однозначное число, каждая цифра множителя умножается на трехзначное число по очереди, начиная с единиц. Например:

• 123 * 4 = 492
• 789 * 5 = 3945

При делении трехзначного числа на однозначное число, деление также производится по разрядам, начиная с сотен. Если результатом деления получается число с остатком, остаток записывается после запятой. Например:

• 987 / 3 = 329
• 543 / 6 = 90,5

Таким образом, трехзначные числа в арифметических операциях обрабатываются по правилам сложения, вычитания, умножения и деления в зависимости от вида операции.

Трехзначное число в геометрии

В геометрии трехзначное число может представлять различные объекты, такие как углы, длины отрезков или площади фигур.

Например, трехзначное число может указывать на меру угла. Угол может быть измерен в градусах или радианах, и трехзначное число может указывать на величину этого угла. Например, угол в 120 градусов будет представлен трехзначным числом 120.

Трехзначное число также может указывать на длину отрезка. Например, отрезок длиной 357 единиц будет представлен трехзначным числом 357.

Еще одним примером трехзначного числа в геометрии может быть площадь фигуры. Площадь фигуры может быть измерена в квадратных единицах, и трехзначное число может указывать на величину площади. Например, площадь квадрата со стороной 456 единиц будет представлена трехзначным числом 456.

Таким образом, трехзначное число в геометрии может использоваться для представления различных характеристик геометрических объектов, таких как углы, длины отрезков или площади фигур.

Вопрос-ответ:

Что такое трехзначное число в математике?

Трехзначное число — это число, которое состоит из трех цифр и находится в диапазоне от 100 до 999.

Можете привести примеры трехзначных чисел?

Конечно! Примерами трехзначных чисел могут быть 123, 456, 789 и так далее.

Как определить, является ли число трехзначным?

Чтобы определить, является ли число трехзначным, нужно посмотреть, состоит ли оно из трех цифр и находится ли в диапазоне от 100 до 999.

Все ли трехзначные числа могут быть записаны в троичной системе счисления?

Нет, не все трехзначные числа могут быть записаны в троичной системе счисления. Например, число 100 в десятичной системе счисления будет записано как 10201 в троичной системе.

Можно ли найти сумму всех трехзначных чисел?

Да, можно найти сумму всех трехзначных чисел. Сумма всех трехзначных чисел равна 494550.

Трехзначное число в комбинаторике

В комбинаторике, трехзначное число обозначает число, состоящее из трех цифр. В отличие от обычного понятия трехзначного числа в математике, трехзначное число в комбинаторике не обязательно имеет десятичное представление. Оно может быть представлено в различных системах счисления, таких как двоичная, восьмеричная или шестнадцатеричная системы.

Когда речь идет о трехзначном числе в комбинаторике, часто имеется в виду число, в котором каждая цифра может принимать значения от 0 до 9. Такое число может быть интерпретировано как комбинация трех элементов из десяти возможных. Например, число 123 можно рассматривать как комбинацию трех элементов, где первая цифра 1, вторая цифра 2 и третья цифра 3.

Однако, в комбинаторике трехзначное число может также иметь другое значение. Например, в двоичной системе счисления число 101 может быть интерпретировано как трехзначное число. В этом случае, каждая цифра может быть либо 0, либо 1, и число 101 может быть рассматриваться как комбинация из трех элементов, где первая цифра 1, вторая цифра 0 и третья цифра 1.

Трехзначные числа в комбинаторике имеют широкое применение в различных областях, таких как теория вероятностей, шифрование и компьютерные науки. Они используются для представления и манипулирования информацией, а также для разработки алгоритмов и решения задач.

Примеры трехзначных чисел в комбинаторике:

123

456

789

Видео по теме: