Что такое произведение цифр в математике

Произведение цифр в математике представляет собой операцию умножения, при которой перемножаются все цифры числа. Узнайте, как вычислять произведение цифр и как это применяется в различных математических задачах.

Произведение цифр является одним из основных понятий в математике. Это операция, которая применяется к числам и представляет собой умножение всех цифр, входящих в состав данного числа. Таким образом, произведение цифр позволяет получить новое число, которое является результатом умножения всех цифр исходного числа.

Наиболее простым примером произведения цифр является число 123. В данном случае, произведение цифр равно 1 * 2 * 3 = 6. То есть, произведение цифр числа 123 равно 6. Для числа 1234 произведение цифр будет равно 1 * 2 * 3 * 4 = 24. Аналогично, для числа 5678 произведение цифр составит 5 * 6 * 7 * 8 = 1680.

Произведение цифр находит свое применение не только в математике, но и в других науках, таких как физика, химия и информатика. Оно позволяет анализировать и взаимодействовать с различными числовыми данными. Например, в информатике произведение цифр может использоваться для проверки чисел на делимость, а также для решения задач по поиску палиндромов или чисел Армстронга.

В заключение, произведение цифр является важным понятием в математике и имеет широкое применение в различных областях науки. Оно позволяет анализировать и манипулировать с числовыми данными, а также решать разнообразные задачи. Знание и понимание этого понятия помогает развивать логическое и аналитическое мышление, а также находить решения для сложных математических проблем.

Что такое произведение цифр?

Произведение цифр может использоваться для решения различных задач в математике. Например, оно может быть полезно при определении кратности числа или при нахождении цифровых корней. Также произведение цифр может быть использовано для проверки правильности набора цифр или для генерации различных комбинаций чисел.

Произведение цифр может быть вычислено как с помощью программного кода, так и вручную. Для вычисления произведения цифр необходимо последовательно умножать все цифры числа друг на друга. В случае, если в числе присутствует ноль, произведение цифр будет равно нулю, так как любое число, умноженное на ноль, равно нулю.

Использование произведения цифр позволяет более глубоко исследовать структуру числа и его составляющих. Этот математический метод является важной составляющей в анализе чисел и может быть применен в различных областях, включая алгебру, геометрии и теорию чисел.

Определение произведения цифр

Для любого натурального числа, состоящего из цифр a1a2a3…an, произведение цифр можно выразить следующим образом:

ЧислоПроизведение цифр

a1a2a3…an

a1 * a2 * a3 * … * an

Например, для числа 1234 произведение цифр будет равно 1 * 2 * 3 * 4 = 24.

Произведение цифр может быть полезно при решении различных задач, например, при проверке числа на делимость, определении кратности и других математических операциях.

Как вычислить произведение цифр?

1. Возьмите число, цифры которого вы хотите перемножить.

2. Разделите число на отдельные цифры. Для этого можно использовать деление по модулю 10. Например, число 12345 разделится на цифры 1, 2, 3, 4 и 5.

3. Умножьте все полученные цифры между собой. Например, для числа 12345 произведение цифр будет равно 1 * 2 * 3 * 4 * 5 = 120.

Некоторые примеры:

Для числа 123: 1 * 2 * 3 = 6

Для числа 456: 4 * 5 * 6 = 120

Для числа 789: 7 * 8 * 9 = 504

Таким образом, вычисление произведения цифр позволяет получить результат, равный перемножению всех цифр данного числа.

Пример вычисления произведения цифр

Для наглядности предположим, что у нас есть число 12345. Чтобы вычислить произведение его цифр, необходимо умножить все цифры между собой. В данном случае:

1 * 2 * 3 * 4 * 5 = 120.

Таким образом, произведение цифр числа 12345 равно 120.

Свойства произведения цифр

Вот некоторые свойства произведения цифр:

СвойствоОписаниеПример

Произведение цифр числа всегда больше или равно нулю.	Произведение цифр числа не может быть отрицательным.	Произведение цифр числа 1234: 1 * 2 * 3 * 4 = 24.
Произведение цифр нуля равно нулю.	Если в числе есть цифра ноль, то произведение цифр будет равно нулю.	Произведение цифр числа 1023: 1 * 0 * 2 * 3 = 0.
Произведение цифр единицы равно самой единице.	Если в числе есть только цифра один, то произведение цифр будет равно единице.	Произведение цифр числа 111: 1 * 1 * 1 = 1.
Произведение цифр числа равно самому числу, если число однозначное.	Если число состоит из одной цифры, то произведение цифр будет равно этой цифре.	Произведение цифр числа 5: 5 = 5.

Знание свойств произведения цифр помогает в решении различных задач и облегчает анализ числовых данных.

Коммутативность произведения цифр

Например, при перемножении цифр 2 и 3 получается результат 6. Это можно записать как 2 * 3 = 6. Из этого выражения видно, что порядок цифр в произведении не важен. То есть, результат будет таким же, если поменять местами цифры: 3 * 2 = 6.

Коммутативность произведения цифр широко используется в различных математических операциях и задачах. Например, при вычислении площади прямоугольника, не важно, какая из его сторон будет обозначаться первой, а какая второй. Важно лишь перемножить размеры сторон, и результат будет одинаковым.

Также коммутативность произведения цифр может быть использована при решении задач по комбинаторике. Например, при вычислении количества возможных перестановок объектов, порядок элементов не важен, и можно воспользоваться коммутативностью произведения цифр для упрощения вычислений.

В заключение, коммутативность произведения цифр является важным свойством математических операций, которое позволяет упростить вычисления и решение задач. Знание этого свойства помогает лучше понять и применять математические концепции в различных областях.

Ассоциативность произведения цифр

Пусть у нас есть три числа: а, b и c. Тогда ассоциативность произведения цифр можно записать следующим образом:

(а * b) * c = а * (b * c)

Это означает, что результат умножения трех чисел будет одинаковым, независимо от того, в каком порядке мы будем их умножать. Например:

2 * (3 * 4) = 2 * 12 = 24

(2 * 3) * 4 = 6 * 4 = 24

Таким образом, ассоциативность произведения цифр позволяет нам упрощать выражения и сокращать количество операций.

Произведение цифр в различных областях математики

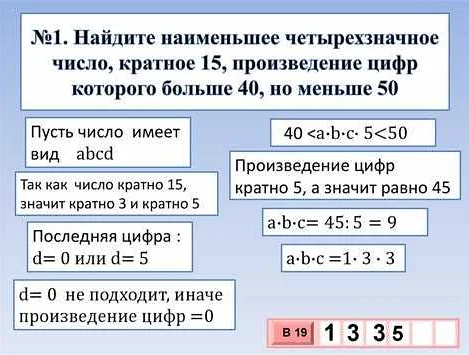
В арифметике произведение цифр используется для определения общего произведения чисел, а также для анализа свойств чисел и выражений.

В теории чисел произведение цифр может использоваться для изучения свойств простых чисел, например, для определения простого числа на основе свойств его цифр.

В математическом анализе и алгебре произведение цифр может быть полезным при решении уравнений и систем уравнений, а также при анализе свойств функций.

В теории вероятности и статистике произведение цифр может использоваться для анализа случайных величин и исследования их свойств.

Произведение цифр также может быть применимо в компьютерной науке и криптографии, где используется для шифрования и дешифрования данных.

В заключение, произведение цифр является важной математической операцией, которая находит применение в различных областях математики и имеет широкий спектр применений.

Произведение цифр в алгебре

Произведение цифр может быть полезно при решении различных задач, таких как нахождение делителей числа, проверка числа на простоту, определение суммы цифр числа и других операций.

Примеры произведения цифр:

• Для числа 123 произведение его цифр равно 1 * 2 * 3 = 6.
• Для числа 4567 произведение его цифр равно 4 * 5 * 6 * 7 = 840.
• Для числа 98765 произведение его цифр равно 9 * 8 * 7 * 6 * 5 = 15120.

Использование произведения цифр позволяет сократить вычисления и облегчить анализ чисел в алгебре.

Вопрос-ответ:

Что такое произведение цифр?

Произведение цифр — это результат умножения двух или более цифр между собой.

Как вычислить произведение цифр?

Для вычисления произведения цифр необходимо умножить каждую цифру, указанную в задаче, на остальные цифры и затем сложить полученные произведения. Например, если нужно вычислить произведение цифр числа 123, то мы умножаем 1 на 2 и на 3, а затем складываем результаты: 1 * 2 * 3 = 6.

В каких задачах можно использовать произведение цифр?

Произведение цифр часто используется в задачах, связанных с комбинаторикой, вероятностью и числами. Например, произведение цифр может быть использовано для вычисления количества возможных комбинаций в различных задачах или для определения вероятности наступления определенного события.

Можете привести пример задачи, в которой используется произведение цифр?

Конечно! Представим, что у нас есть 3 различных карточки, на каждой из которых написана одна из цифр 1, 2 или 3. Мы хотим узнать, сколько всего возможных комбинаций можно составить, используя эти карточки. Для этого мы можем использовать произведение цифр: количество комбинаций равно произведению количества вариантов для каждой цифры, то есть 3 * 2 * 1 = 6 комбинаций.

Можно ли использовать произведение цифр для решения задачи на вероятность?

Да, можно. Например, предположим, что у нас есть мешок с 5 шарами, пронумерованными от 1 до 5. Мы случайным образом вытаскиваем один шар. Вероятность того, что вытащим шар с четной цифрой, можно рассчитать, используя произведение цифр: 2 и 4 являются четными цифрами, поэтому вероятность равна 2/5, так как у нас 2 возможных четных цифры из 5 возможных вариантов.

Что такое произведение цифр в математике?

Произведение цифр в математике — это результат умножения двух или более цифр. Например, произведение цифр 3 и 4 равно 12.

Какую роль играют произведение цифр в математике?

Произведение цифр в математике играет важную роль в различных операциях и задачах. Например, оно используется для умножения чисел и нахождения общего кратного. Кроме того, произведение цифр может быть использовано для нахождения числа цифр в числе или определения свойств чисел.

Произведение цифр в теории вероятностей

Рассмотрим пример. Пусть у нас есть число 456. Чтобы найти произведение цифр этого числа, нам необходимо умножить 4 на 5 на 6, что равно 120.

Произведение цифр может быть полезно при решении различных задач в теории вероятностей. Например, при вычислении вероятности того, что в результате броска двух кубиков выпадет определенная комбинация чисел.

Для более наглядного представления произведения цифр можно использовать таблицу. Ниже приведена таблица, которая показывает произведение цифр для некоторых чисел:

ЧислоПроизведение цифр

123	6
456	120
789	504

Таким образом, произведение цифр является важной операцией в теории вероятностей и может использоваться для вычисления вероятностей различных событий.

Видео по теме: