Что такое три четверти в математике
Содержимое
- 1 Что такое три четверти в математике
- 1.1 Определение три четверти в математике
- 1.2 Три четверти: концепция и применение
- 1.3 Три четверти в геометрии
- 1.4 Примеры использования три четверти в математике
- 1.5 Три четверти и дроби
- 1.6 Три четверти в процентах
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое три четверти в математике?
- 1.8.0.2 Как можно представить три четверти в виде десятичной дроби?
- 1.8.0.3 Какая десятичная дробь эквивалентна трем четвертым?
- 1.8.0.4 Можно ли сократить три четверти?
- 1.8.0.5 Как можно представить три четверти с помощью геометрической модели?
- 1.8.0.6 Что такое три четверти в математике?
- 1.9 Задания с использованием три четверти
- 1.10 Выводы о три четверти в математике
Три четверти в математике — это понятие, которое обозначает одну третью или 75% от целого. Это важное понятие, используемое в различных вычислениях и задачах. Узнайте больше о том, что такое три четверти и как его использовать в математике.
Три четверти — это математическое понятие, которое обозначает три части от целого, каждая из которых равна одной четверти. В математике, четверть — это одна из четырех равных частей, на которые можно разделить целое число или предмет. Термин «три четверти» означает, что имеется три таких равных части, которые в сумме составляют три четверти или 75% от целого.
Примеры использования термина «три четверти» в математике:
1. Если у вас есть пирог, и вы съели три четверти от него, то осталась только одна четверть. В этом случае можно сказать, что вы съели 75% пирога.
2. Рассмотрим еще один пример: если у вас есть час, и за первые три четверти часа вы выполнили задание, то осталось выполнить только одну четверть задания. Это означает, что вы уже сделали 75% работы.
Таким образом, понятие «три четверти» в математике относится к трем равным частям, каждая из которых составляет одну четверть или 25% от целого. Это понятие применяется в различных областях, где важно определить долю или процент от целого.
Определение три четверти в математике
Три четверти в математике представляют собой меру, равную трем четвертям или трем четвертым части от целого. Это означает, что при делении целого на четыре равные части, три из этих частей будут составлять три четверти.
Три четверти можно представить в виде десятичной дроби — 0.75 или в виде процента — 75%. Они также могут быть представлены в виде обыкновенной дроби — 3/4.
Примеры использования три четверти в математике включают расчеты вероятности, доли или долей, а также разделение объектов или количества на равные части.
Три четверти: концепция и применение
Применение концепции три четверти может быть найдено в различных областях. Например, в рецептах кулинарии, 3/4 часть ингредиентов может быть представлена в виде трех четвертей, чтобы облегчить процесс мерения и смешивания. Также, во время выполнения музыкальных произведений, ритм может быть разделен на три равные части, каждая из которых составляет одну четверть.
Другой пример применения три четверти в математике может быть найден в статистике, где 3/4 может использоваться для описания процента или части, соответствующей трем четвертям от общего числа наблюдений. Таким образом, три четверти могут быть полезны для анализа данных и описания их доли.
Итак, концепция три четверти имеет широкое применение и может быть использована для описания долей, отношений и процентов в различных сферах жизни.
Три четверти в геометрии
В геометрии понятие «три четверти» относится к разделению отрезка или круга на три равные части. Это может быть полезно при решении задач, связанных с построением или измерением фигур.
Например, если у нас есть отрезок длиной 12 сантиметров, то мы можем разделить его на три равные части, каждая из которых будет составлять 4 сантиметра.
В случае круга, три четверти означают деление его на три равных дуги. Если у нас есть круг с общей длиной окружности 36 сантиметров, то каждая дуга будет составлять 12 сантиметров.
Три четверти в геометрии являются одной из основных концепций, используемых для разделения фигур на равные части и решения геометрических задач.
Примеры использования три четверти в математике
ПримерРасчет три четверти
| Пример 1 | Если у нас есть пирог, разделенный на четыре равные части, то три четверти пирога будет составлять три из этих частей. |
| Пример 2 | Если у нас есть круг, то три четверти круга будет равняться углу 270 градусов, так как полный угол в круге составляет 360 градусов. |
| Пример 3 | Если у нас есть линия, разделенная на четыре равные части, то три четверти этой линии будет составлять три из этих частей. |
Таким образом, три четверти является удобным способом представления равных долей целого в математике и применяется в различных задачах и ситуациях.
Три четверти и дроби
Три четверти также можно представить в виде десятичной дроби — 0,75. Это означает, что три четверти составляют 75 процентов от целого.
Примеры использования три четверти и дробей можно найти в различных ситуациях. Например, если у вас есть пирог, и вы съели три из четырех частей, то вы съели три четверти пирога.
Три четверти также может быть использовано для представления времени. Если час прошел, и осталась три четверти часа, это означает, что осталось 45 минут до полного часа.
- Три четверти + одна четверть = целое
- Три четверти < восьми четвертей
- Три четверти > двух четвертей
Три четверти и дроби — важные понятия в математике, которые могут быть использованы для представления частей целого и долей времени, а также в других различных контекстах.
Три четверти в процентах
3/4 × 100 = 75%
Таким образом, три четверти равны 75 процентам. Это значит, что если у нас есть целое число, то три четверти от него будут составлять 75% от этого числа.
Например, если у нас есть 100 рублей, то три четверти от этой суммы будут составлять 75 рублей.
Три четверти в процентах также используются для обозначения вероятности. Если у нас есть какое-то событие, и оно имеет вероятность 3/4, то можно сказать, что это событие имеет вероятность 75%.
Таким образом, три четверти в процентах равны 75% и используются для выражения долей или вероятностей.
Видео по теме:
Вопрос-ответ:
Что такое три четверти в математике?
Три четверти в математике — это дробь, равная трем четвертым от целого.
Как можно представить три четверти в виде десятичной дроби?
Три четверти в виде десятичной дроби равны 0.75.
Какая десятичная дробь эквивалентна трем четвертым?
Три четверти эквивалентны десятичной дроби 0.75.
Можно ли сократить три четверти?
Нет, три четверти нельзя сократить, так как числитель и знаменатель не имеют общих делителей.
Как можно представить три четверти с помощью геометрической модели?
Три четверти можно представить с помощью круга, разделенного на четыре равные части, где три из четырех частей будут закрашены.
Что такое три четверти в математике?
Три четверти в математике — это выражение, которое означает три части от целого, равные четверти. В математическом понимании, одна четверть равна 1/4 или 25% от целого. Таким образом, три четверти представляют собой 3/4 или 75%.
Задания с использованием три четверти
Примеры заданий, в которых используются три четверти:
- Задача на вычисление: Если весь пирог был разделен на четыре равные части, и я съел три из них, какая часть пирога осталась?
- Задача на сравнение: В классе 25 учеников, из которых 3/4 ходят в спортивную секцию. Сколько учеников ходит в спортивную секцию?
- Задача на проценты: В магазине проводится распродажа, на которую скидка составляет 75% от общей стоимости. Какую сумму нужно заплатить, если исходная цена товара была 1000 рублей?
- Задача на вероятность: В колоде из 52 карты 39 карт являются червами. Какова вероятность вытянуть из колоды три червовые карты подряд?
Это лишь некоторые примеры заданий, в которых можно использовать три четверти. В математике эта доля широко применяется для решения различных задач, связанных с долями, долями и процентами или вероятностью.
Выводы о три четверти в математике
Три четверти можно представить в виде десятичной дроби, которая равна 0,75.
Три четверти также можно представить в процентном виде, где они эквивалентны 75%.
Примеры использования три четверти:
— Если у нас есть пирог, и мы съели 3 из 4 частей, то мы съели три четверти пирога. Это можно записать как 3/4 или 0,75 или 75%.
— Если у нас есть 12 яблок и мы отдаем 3 четверти яблок другу, то мы отдаем ему 9 яблок. Это можно записать как 3/4 или 0,75 или 75% от всех яблок.
— Если у нас есть 24 часа, и мы проводим 3 четверти времени на учебу, то мы проводим 18 часов на учебу. Это можно записать как 3/4 или 0,75 или 75% от всех часов.


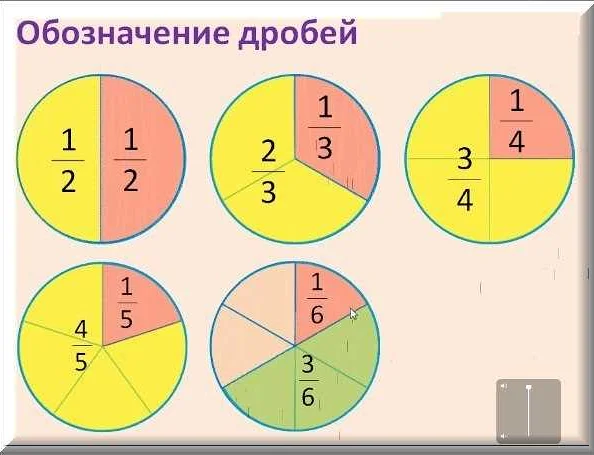

Три четверти — это дробное число, которое равно трем четвертям целого. В математике три четверти обозначается как 3/4 или 0.75 в десятичном представлении. Данная дробь показывает, что объект или количество разделено на четыре равные части, и мы берем три из этих частей. Примеры использования три четверти в повседневной жизни могут быть разнообразными. Например, представьте, что у вас есть пирог, и вы съели три четверти этого пирога. Это означает, что вы съели три равные части из четырех, а оставшаяся четверть пирога осталась нетронутой. Другой пример — футбольное поле. Если вы находитесь на одной трети поля и переходите на три четверти поля, это означает, что вы прошли почти всю его длину. Таким образом, понимание три четверти в математике помогает нам делить объекты на равные части и использовать эту информацию в различных контекстах. Это важное понятие для решения задач и повседневного применения математики.
Статья очень интересно и доступно рассказывает о таком понятии, как «три четверти» в математике. Я, как женщина, всегда интересовалась математикой и часто сталкивалась с этим термином, но у меня всегда были сомнения в его точном определении. Статья помогла мне понять, что три четверти — это обозначение для числа, равного трем четвертым или трем четвертям. Таким образом, три четверти можно записать как 3/4 или 0.75. Очень полезным было объяснение о том, как вычислять три четверти от числа. Например, чтобы найти три четверти от числа 12, нужно умножить 12 на 3/4 или 0.75. Это даёт нам результат 9. Теперь я знаю, что три четверти от числа — это просто 75% от него. Статья также приводит примеры использования три четверти в практических задачах. Например, в кулинарии, когда нужно отмерить определенное количество ингредиентов. Также три четверти можно использовать для определения времени, например, когда нужно рассчитать, сколько времени займет выполнение задачи, занимающей три четверти от общего времени. В целом, статья очень понятно и ясно объясняет, что такое три четверти в математике, и как его можно использовать в практических ситуациях. Я получила ответы на свои вопросы и расширила свои знания в этой области. Очень рекомендую всем, кто интересуется математикой и хочет расширить свой кругозор.