Что значит три четверти в математике

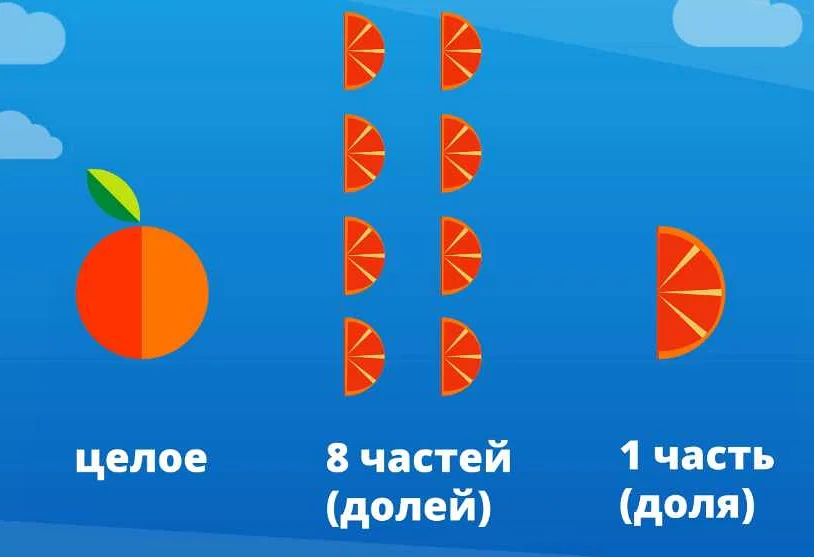
Три четверти в математике означают три из четырех одинаковых частей, на которые можно разделить целое число или объект. Узнайте, как работать с тремя четвертями и решать задачи с их использованием в математике.

Три четверти — это понятие из области математики, которое используется для обозначения дробей или долей. Три четверти означает, что мы имеем дело с дробью, равной трем четвертым или трем четвертым целой единицы. В математике дроби часто используются для представления частей целого числа, когда целое число не может быть разделено на равные части.

Три четверти можно записать в виде десятичной дроби — 0.75, а также в виде процента — 75%. Они также могут быть представлены в виде обыкновенной дроби — 3/4.

Использование три четверти в математике может быть очень полезным во многих ситуациях. Например, если у нас есть пирог, который разделен на четыре равные части, то три четверти означает, что мы взяли три из этих четырех частей. Три четверти также могут быть использованы для выражения вероятности — например, если вероятность события равна 75%, то это означает, что из 100 возможных исходов, это событие произойдет в 75 случаях.

Три четверти также могут быть использованы для измерения времени. Например, если час разделен на четыре равные части, то три четверти часа означает, что прошло 45 минут. Это может быть полезно при планировании или измерении времени в различных ситуациях.

В заключение, три четверти — это важное понятие в математике, которое используется для обозначения дробей и долей. Оно может быть представлено в виде десятичной дроби, процента или обыкновенной дроби. Использование три четверти может быть полезным в различных ситуациях, таких как измерение времени, выражение вероятности или разделение объектов на равные части.

Понятие три четверти

В математике понятие «три четверти» относится к дробям и процентам. Оно указывает на то, что количество или значение представлено в третьей части от целого.

Три четверти в дробном виде обозначаются как 3/4 или 0,75. В данном случае числитель равен 3, что означает, что имеется 3 единицы измерения, а знаменатель равен 4, что означает, что единица измерения разделена на 4 равные части.

Три четверти также могут быть выражены в процентах. В данном случае, 3/4 равно 75%. Это означает, что из целого значения, 75% принадлежит к трем четвертям.

Понятие три четверти в математике может быть использовано для представления долей, доли времени или доли поверхности. Например, если у вас есть пирог, разделенный на 4 части, то 3 четверти пирога будет означать, что осталась 1 четверть или 25% пирога.

Три четверти также могут использоваться для описания времени. Если у вас есть час, поделенный на 4 равные части, то 3 четверти часа будет равно 45 минутам.

Таким образом, понятие три четверти в математике является важным для понимания долей и процентов. Оно помогает нам представлять количество или значение в третьей части от целого.

Видео по теме:

История возникновения

Понятие «три четверти» в математике возникло в древнем Египте, где делились песчаные часы на четыре равные части. Одна из этих частей, составляющая три четверти от общего времени, стала называться «три четверти».

В дальнейшем, это понятие было внедрено в математику и получило более точное определение. Три четверти обозначают три равные части от целого, которые в сумме составляют 75%.

Три четверти широко используются в различных областях, таких как статистика, финансы и процентные расчеты. Они позволяют представить долю или доли от целого числа и упрощают математические вычисления.

Значение в математике

В математике понятие «значение» относится к численному результату вычислений или оценки выражения. Оно используется для определения конкретных чисел или точек на числовой оси.

В контексте три четверти, значение обычно относится к дробям или числам, которые представлены в виде отношения целых чисел, таких как 3/4. Значение такой дроби равно числу, которое получается при разделении числителя на знаменатель.

Например, если мы имеем дробь 3/4, то значение этой дроби равно 0,75. Это число представляет собой три четверти от единицы.

Значение в математике также может относиться к результату функции. Функция — это математическое правило, которое преобразует одно число в другое. Значение функции является численным результатом, полученным при подстановке определенного значения в функцию.

Например, если у нас есть функция f(x) = 2x + 3, то значение функции при x = 4 будет равно 2*4 + 3 = 11. Таким образом, значение функции при x = 4 равно 11.

Значение в математике играет важную роль при решении уравнений, оценке выражений и анализе данных. Оно позволяет нам получить конкретные численные результаты, которые можно использовать для принятия решений или сравнения различных значений.

Вопрос-ответ:

Что такое три четверти в математике?

Три четверти в математике – это то же самое, что и три четвертых. Это дробное число, которое равно 3/4 или 0.75. Оно означает, что из целого числа было взято три равные части из четырех возможных.

Как использовать три четверти в математике?

В математике три четверти можно использовать для различных расчетов. Например, если у вас есть целое число, вы можете умножить его на три четверти, чтобы найти 75% от этого числа. Также, вы можете использовать три четверти для представления доли чего-либо, например, если у вас есть торт, и вы хотите разделить его на части, то три четверти будут означать три из четырех равных кусочков.

Можно ли представить три четверти в виде десятичной дроби?

Да, три четверти можно представить в виде десятичной дроби. Она будет равна 0.75. Это значит, что из целого числа было взято три равные части из четырех возможных. Один целый кусок составляет 0.25, поэтому три кусочка будут равны 0.75.

Как найти три четверти от числа?

Чтобы найти три четверти от числа, нужно это число умножить на 0.75 или на 3/4. Например, если у вас есть число 100, то три четверти от него будут равны 75. Для этого нужно умножить 100 на 0.75 или на 3/4. Получится 75, что составляет три четверти от 100.

Как можно представить три четверти геометрически?

Геометрически три четверти можно представить с помощью круга или прямоугольника. Если мы возьмем круг и разделим его на четыре равные части, то три из этих четырех частей будут составлять три четверти круга. Аналогично, если мы возьмем прямоугольник и разделим его на четыре равные части, то три из этих четырех частей будут составлять три четверти прямоугольника.

Что такое три четверти в математике?

В математике три четверти представляют собой дробь, равную трем четвертым или трем частям от целого. Три четверти можно записать как 3/4 или 0,75 в десятичной форме. Это означает, что целое число разделено на четыре равные части, и три из них составляют три четверти.

Как можно использовать три четверти в математике?

Три четверти могут быть использованы в самых разных ситуациях. Например, если у вас есть пирог, вы можете разделить его на четыре равные части и взять три из них, чтобы представить три четверти пирога. Это может быть полезно, если вы хотите поделиться пирогом с тремя друзьями, и каждый из вас будет получать одинаковую часть. Три четверти также могут использоваться для представления процентного соотношения, например, если у вас есть 100 яблок и 3/4 из них — это зеленые яблоки, то это означает, что 75 из 100 яблок зеленые.

Применение в статистике

Три четверти играют важную роль в статистике, особенно в анализе данных и построении графиков. Они помогают нам понять, как данные распределены и какую часть они занимают в общей выборке.

Одним из основных способов использования три четверти является построение ящика с усами (box and whisker plot). Ящик с усами позволяет визуализировать основные характеристики выборки, такие как медиана, нижний и верхний квартили, а также выбросы.

Медиана, или второй квартиль, представляет собой значение, которое делит выборку на две равные части. Она находится точно посередине между первым и третьим квартилями. Первый квартиль, или нижний квартиль, разделяет нижнюю четверть выборки от остальных значений. Третий квартиль, или верхний квартиль, разделяет верхнюю четверть выборки от остальных значений.

Построение ящика с усами позволяет наглядно увидеть, как распределены данные, какая часть значений сосредоточена внутри интерквартильного диапазона (между первым и третьим квартилями) и какие значения являются выбросами. Это может помочь в определении распределения данных, обнаружении необычных значений и сравнении нескольких выборок.

Также три четверти используются для вычисления межквартильного размаха (interquartile range), который позволяет оценить разброс данных внутри интерквартильного диапазона. Межквартильный размах определяется вычитанием первого квартиля из третьего квартиля.

В статистике три четверти являются удобным инструментом для анализа данных и визуализации их распределения. Они помогают нам лучше понять характеристики выборки и выделить основные особенности данных.

Применение в геометрии

Например, если у нас есть круг, то 3/4 этого круга будет означать, что круг разделен на 4 равные части, и 3 из этих частей будут заполнены. Таким образом, 3/4 круга будет означать, что круг заполнен на 75%.

Также три четверти могут использоваться для определения площади прямоугольника. Если у нас есть прямоугольник со сторонами a и b, то площадь этого прямоугольника равна a*b. Если мы хотим найти площадь прямоугольника, заполненного три четвертями, то мы можем умножить площадь всего прямоугольника на 3/4.

Применение три четверти в геометрии может быть полезным при решении различных задач, связанных с определением площадей и долей фигур. Оно позволяет нам более точно описывать и измерять различные геометрические объекты.

Как использовать три четверти

Одним из применений три четверти является представление времени. Например, если вам нужно представить время половины часа, вы можете использовать три четверти. В одном часе 60 минут, а половина часа составляет 30 минут. Поэтому, чтобы представить половину часа с использованием три четверти, вы можете записать это как 45 минут (так как 30 * 3/4 = 45).

Другим примером использования три четверти является представление доли чего-либо. Например, если у вас есть 100 яблок и вы хотите представить три четверти от этого количества, вы можете умножить 100 на 3/4 и получить 75 яблок — три четверти от исходного количества.

Также стоит отметить, что три четверти можно представить в виде десятичной дроби. Для этого нужно разделить числитель (3) на знаменатель (4). В результате получится 0.75, что означает 75 процентов или три четверти.

Использование три четверти в математике помогает нам представлять различные доли и части целого. Этот способ особенно полезен при решении задач, связанных с долями, временем и процентами.

Расчет величин

Для расчета величин в три четверти необходимо знать общую величину и разделить ее на три равные части. Например, если у нас есть отрезок длиной 12 единиц, то одна четверть составляет 12 / 4 = 3 единицы, а три четверти — это 3 * 3 = 9 единиц.

Три четверти могут быть использованы для расчета долей, доли целого числа или процентного соотношения. Например, если мы хотим вычислить 75% от некоторой величины, мы можем использовать три четверти как приближение. В этом случае мы умножаем общую величину на 0.75 (три четверти) и получаем искомую величину.

Также три четверти могут быть использованы для расчета временных интервалов. Например, если у нас есть часовой интервал длительностью 60 минут, то одна четверть этого интервала составляет 60 / 4 = 15 минут, а три четверти — это 15 * 3 = 45 минут.

В заключение, три четверти — это удобная и полезная фракция, которая позволяет легко и точно расчитывать величины, доли и временные интервалы. Она находит широкое применение в различных областях математики, физики, экономики, а также в повседневной жизни.

Анализ данных

Существует несколько методов анализа данных:

1. Описательный анализ данных — представление и интерпретация данных с помощью статистических показателей, таких как среднее значение, медиана и стандартное отклонение. Этот вид анализа помогает понять основные характеристики данных и их распределение.
2. Кластерный анализ данных — группировка схожих объектов или наблюдений в отдельные кластеры. Этот метод позволяет выявить скрытые паттерны и группы в данных, что может быть полезно для сегментации клиентов, поиска аномалий или классификации данных.
3. Прогнозирование и предсказание — использование статистических моделей и алгоритмов машинного обучения для предсказания будущих значений или событий на основе имеющихся данных. Прогнозы могут быть использованы для оптимизации запасов, планирования производства или прогнозирования спроса.
4. Ассоциативный анализ данных — выявление связей и взаимосвязей между различными переменными в наборе данных. Ассоциативный анализ может помочь в поиске скрытых зависимостей, например, между покупками товаров или поведением пользователей.
5. Визуализация данных — представление данных в графическом или графическом виде для лучшего восприятия и понимания. Визуализация данных может помочь выявить тренды, аномалии и паттерны, которые не всегда заметны при простом анализе числовых значений.

Анализ данных играет важную роль в различных сферах, таких как бизнес, медицина, финансы, маркетинг и наука. Он позволяет принимать обоснованные решения и улучшать результаты деятельности, основанные на фактах и информации.

Построение графиков

Для построения графика необходимо иметь набор значений переменных, для которых вычисляются соответствующие значения функции. Затем эти точки отмечаются на графике и соединяются линией. Таким образом, с помощью графика можно наглядно увидеть изменение функции в зависимости от значений переменных.

Для построения графиков в математике широко используется таблица значений. В таблице значения переменных записываются в первом столбце, а соответствующие значения функции – во втором столбце. Затем эти точки отмечаются на графике и соединяются линией.

Построение графика позволяет анализировать функции и исследовать их свойства. Например, с помощью графика можно определить максимальное и минимальное значение функции, найти точки пересечения с осями координат, определить периодичность функции и т.д.

Графики широко используются в различных областях науки и техники, таких как физика, экономика, биология и другие. Они позволяют визуализировать сложные зависимости и делают математические модели легче понятными.

Значение переменнойЗначение функции

1	3
2	5
3	7
4	9

Применение в финансовых расчетах

В финансовых расчетах три четверти могут использоваться для определения процентов от суммы или для разбиения времени на участки, например, в расчетах по депозитам или инвестициям.

Например, если вы хотите рассчитать, сколько процентов составляет определенная сумма от общего капитала, вы можете использовать формулу: процент = (сумма / общий капитал) * 100%. Здесь три четверти используются для представления процентов.

Также три четверти могут быть полезны при расчете процентов от долга или при расчете ежемесячных платежей по кредиту. Например, если вы должны выплатить долг в размере 100 000 рублей за три года, вы можете использовать формулу: ежемесячный платеж = (сумма долга / количество месяцев) * (3 четверти). Здесь три четверти представляют собой период времени, равный трем годам.

Три четверти также могут быть полезны при расчете времени, которое требуется для достижения определенной финансовой цели. Например, если вы хотите накопить определенную сумму денег через 5 лет и у вас есть возможность вкладывать каждый месяц 3 четверти вашего дохода, вы можете рассчитать, сколько нужно вкладывать каждый месяц, чтобы достичь цели.

ПримерФормула

Расчет процентов	процент = (сумма / общий капитал) * 100%
Расчет ежемесячного платежа	ежемесячный платеж = (сумма долга / количество месяцев) * (3 четверти)
Расчет времени	время = (накопленная сумма / ежемесячное вложение) / (3 четверти)

Таким образом, использование три четверти в финансовых расчетах позволяет более точно определить проценты, разбить время на участки и рассчитать ежемесячные платежи или вложения.