Что значит возрастания в математике
Содержимое
- 1 Что значит возрастания в математике
- 1.1 Возрастание в математике: определение и примеры
- 1.2 Что такое возрастание в математике?
- 1.3 Как определить возрастание функции?
- 1.4 Как определить точки возрастания функции?
- 1.5 Математические условия возрастания функции
- 1.6 Примеры функций с возрастанием
- 1.7 Как использовать возрастание функции в решении задач?
- 1.8 Значение возрастания функции в реальной жизни
- 1.9 Вопрос-ответ:
- 1.9.0.1 Что такое возрастание в математике?
- 1.9.0.2 Как можно определить, что функция возрастает?
- 1.9.0.3 Какие примеры возрастающих функций можно привести?
- 1.9.0.4 Каким образом возрастание функции отличается от убывания?
- 1.9.0.5 Какое значение имеет возрастание функции в математике?
- 1.9.0.6 Что такое возрастание в математике?
- 1.10 Видео по теме:
Возрастание в математике означает, что последовательность чисел, функция или график увеличиваются по значению. Узнайте, как определить возрастание и применить это понятие в решении задач и анализе данных.
Возрастание — это понятие, которое встречается во многих разделах математики, но особенно важно оно в анализе. Возрастание описывает изменение значения функции по мере увеличения аргумента. Иначе говоря, функция считается возрастающей, если при увеличении аргумента значения функции также увеличиваются.
Определение возрастания можно сформулировать следующим образом: функция f(x) называется возрастающей на промежутке [a, b], если для любых двух точек x1 и x2 из этого промежутка, где x1 < x2, выполняется неравенство f(x1) < f(x2). Аналогично, функция считается строго возрастающей на промежутке [a, b], если для всех x1 и x2 из этого промежутка, где x1 < x2, выполняется строгое неравенство f(x1) < f(x2).
Примерами функций, которые могут быть возрастающими, являются линейная функция f(x) = kx + b, где k > 0, и показательная функция f(x) = a^x, где a > 1. Также можно привести пример функции, которая является строго возрастающей: квадратная функция f(x) = x^2, определенная на промежутке [0, +∞).
Знание понятия возрастания в математике полезно для анализа функций и решения различных задач. Оно позволяет определить, как изменяется функция в зависимости от изменения ее аргумента и использовать это знание для прогнозирования и описания различных явлений в реальном мире.
Возрастание в математике: определение и примеры
Более точно, функция говорится возрастающей на интервале, если для любых двух точек этого интервала, значение функции в первой точке меньше значения функции во второй точке. Математически это можно записать следующим образом:
Для функции f(x), определенной на интервале (a, b), она является возрастающей, если для любых двух точек x1 и x2 из интервала (a, b) таких, что x1 < x2, выполняется неравенство f(x1) < f(x2).
Например, рассмотрим функцию f(x) = x^2. Мы можем заметить, что при увеличении значения аргумента x, значение функции f(x) также увеличивается. Таким образом, функция f(x) = x^2 является возрастающей на всей числовой прямой.
Возрастание в математике — важное понятие, которое используется во многих областях, включая анализ функций, оптимизацию и теорию вероятностей. Понимание этого понятия позволяет нам анализировать и понимать свойства функций и их поведение.
Что такое возрастание в математике?
Чтобы определить возрастание функции, можно рассмотреть её график. Если график функции идёт вверх, то функция возрастает. Например, функция y = x^2 возрастает, так как её график представляет собой параболу, которая открывается вверх и вершина которой находится выше оси абсцисс.
Математически возрастание функции можно записать следующим образом: если для любых двух значений аргумента x1 и x2, при условии x1 < x2, выполняется неравенство f(x1) < f(x2), то функция f(x) возрастает на данном промежутке.
Аргумент (x)Значение функции (f(x))
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
В приведённой выше таблице представлены значения функции f(x) = x^2 для различных значений аргумента x. Заметим, что при увеличении значения x, значение функции также увеличивается. Это означает, что функция возрастает.
Как определить возрастание функции?
В математике, возрастание функции означает, что значения функции увеличиваются при увеличении аргумента.
Для определения возрастания функции можно использовать производную. Если производная функции положительна на некотором интервале, то функция возрастает на этом интервале.
Также можно использовать таблицу значений функции. Если значения функции увеличиваются при увеличении аргумента, то функция возрастает.
Например, для функции f(x) = x^2, производная равна f'(x) = 2x. Производная положительна для всех значений x, кроме x = 0. Следовательно, функция f(x) = x^2 возрастает на всей числовой прямой, кроме точки x = 0.
Таким образом, для определения возрастания функции важно анализировать значение производной на интервалах и использовать таблицу значений функции.
Как определить точки возрастания функции?
В математике точкой возрастания функции называется точка на графике функции, в которой значение функции строго увеличивается по мере движения по оси абсцисс. Иными словами, если в окрестности такой точки все значения функции больше значений слева от нее, то говорят, что функция возрастает в этой точке.
Для определения точек возрастания функции необходимо:
- Найти производную функции.
- Решить неравенство, полученное при приравнивании производной к нулю.
- Построить интервалы возрастания и убывания функции, используя найденные точки.
Полученные точки являются критическими точками функции, в которых может быть локальный максимум или минимум. Для определения, является ли точка максимумом или минимумом, необходимо анализировать знаки производной в окрестностях этих точек.
Например, рассмотрим функцию f(x) = x^2. Ее производная равна f'(x) = 2x. Приравняем производную к нулю: 2x = 0. Получаем x = 0. Таким образом, точка (0, 0) является критической точкой функции. Далее, анализируем знаки производной в окрестности точки x = 0. Если x < 0, то f'(x) < 0, значит функция убывает. Если x > 0, то f'(x) > 0, функция возрастает. Таким образом, точка (0, 0) является точкой минимума функции f(x) = x^2.
Математические условия возрастания функции

1. Производная функции должна быть положительной на данном интервале. Производная функции показывает скорость изменения функции в каждой точке. Если производная положительна на интервале, то функция возрастает.
2. График функции должен иметь положительный наклон на данном интервале. Если наклон графика функции положительный, то функция возрастает.
3. Значения функции должны увеличиваться с увеличением аргумента на данном интервале. Если значения функции возрастают при увеличении аргумента, то функция возрастает.
Все эти условия вместе говорят о том, что функция возрастает на определенном интервале. Они позволяют определить, является ли функция монотонно возрастающей, то есть возрастает на всей области определения.
Пример: рассмотрим функцию f(x) = x^2. Ее производная f'(x) = 2x. Заметим, что производная положительна для всех значений x, кроме нуля. Значит, функция возрастает на интервале (-∞, 0) и (0, +∞). График функции также имеет положительный наклон на этих интервалах. И значения функции увеличиваются с увеличением аргумента на данных интервалах. Таким образом, функция f(x) = x^2 является монотонно возрастающей на всей области определения.
Примеры функций с возрастанием
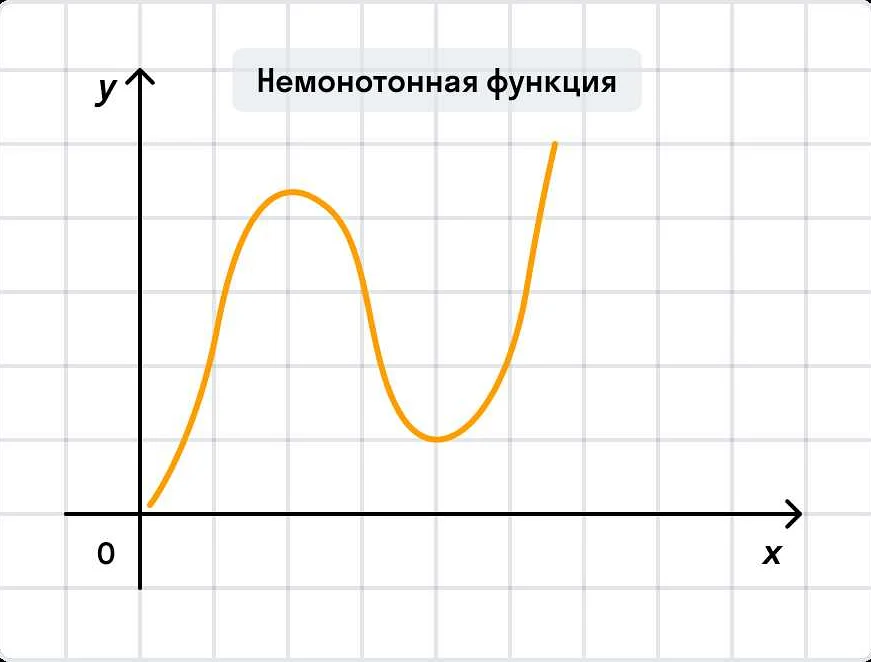
1. Линейная функция: Функция вида f(x) = kx, где k — постоянное число. Например, f(x) = 2x — это линейная функция с возрастанием. При увеличении значения x на единицу, значение функции увеличивается на 2.
2. Квадратичная функция: Функция вида f(x) = ax^2 + bx + c, где a, b, c — постоянные числа. Например, f(x) = x^2 — это квадратичная функция с возрастанием. При увеличении значения x, значение функции увеличивается.
3. Экспоненциальная функция: Функция вида f(x) = a^x, где a — положительное число. Например, f(x) = 2^x — это экспоненциальная функция с возрастанием. При увеличении значения x на единицу, значение функции увеличивается в два раза.
4. Логарифмическая функция: Функция вида f(x) = loga(x), где a — положительное число, a ≠ 1. Например, f(x) = log2(x) — это логарифмическая функция с возрастанием. При увеличении значения x, значение функции увеличивается.
5. Тригонометрическая функция: Некоторые тригонометрические функции могут также быть возрастающими на определенных интервалах. Например, функция f(x) = sin(x) возрастает на интервале от 0 до π.
Это лишь несколько примеров функций с возрастанием. В математике существует много других функций, у которых также есть это свойство. Знание и понимание возрастания функций полезно при изучении и анализе математических моделей и решении задач из различных областей.
Как использовать возрастание функции в решении задач?
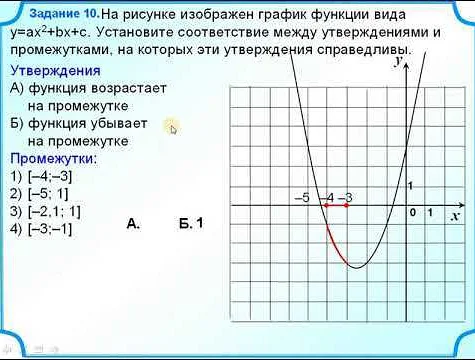
Когда функция возрастает, это означает, что значения функции увеличиваются по мере увеличения аргумента. То есть, если мы увеличиваем значение аргумента, значение функции тоже будет увеличиваться.
Для использования возрастания функции в решении задач, мы можем использовать следующие шаги:
- Определить, что функция является возрастающей на заданном интервале. Для этого мы должны проверить, что производная функции положительна на данном интервале. Если производная положительна, это означает, что функция возрастает.
- Найти значения функции на концах заданного интервала. Если значение функции на левом конце интервала меньше значения функции на правом конце интервала, то функция возрастает на этом интервале.
- Использовать свойства возрастания функции для решения задачи. Например, если нам нужно найти максимальное значение функции на заданном интервале, мы можем использовать информацию о возрастании функции для ограничения поиска только на этом интервале.
Возрастание функции может быть использовано в различных областях математики и ее приложениях. Например, в экономике можно использовать возрастание функции для определения оптимального производства и максимизации прибыли. В физике возрастание функции может быть использовано для определения максимальной скорости движения тела.
Значение возрастания функции в реальной жизни
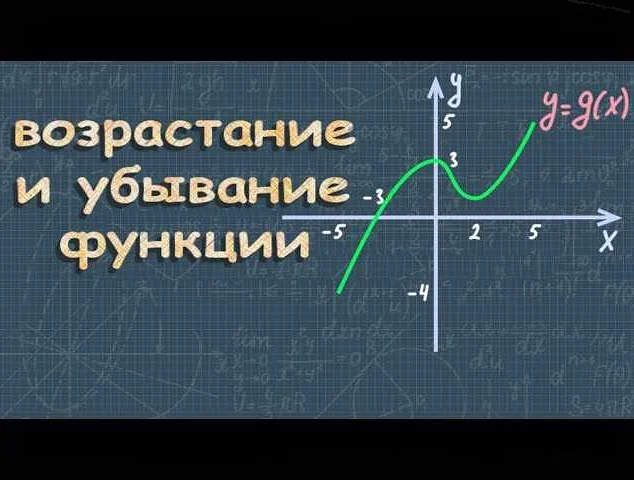
Например, представим себе ситуацию, когда производительность рабочего завода зависит от числа работников. Пусть функция P(n) описывает производительность (P) завода в зависимости от числа работников (n). Если функция P(n) возрастает при увеличении числа работников, это означает, что с увеличением числа работников производительность завода также увеличивается. Таким образом, возрастание функции в данном случае имеет практическое значение, так как позволяет оптимизировать работу завода, увеличивая число работников для повышения производительности.
Другой пример возрастания функции в реальной жизни – это изменение температуры воздуха в зависимости от времени суток. Пусть функция T(t) описывает температуру (T) воздуха в зависимости от времени суток (t). Если функция T(t) возрастает при увеличении времени суток, это означает, что с увеличением времени суток температура воздуха также увеличивается. Такое знание может быть полезно для планирования активностей, связанных с погодными условиями, например, для выбора оптимального времени для прогулки или занятий спортом.
Вопрос-ответ:
Что такое возрастание в математике?
Возрастание — это свойство функции, при котором ее значения увеличиваются по мере увеличения аргумента. То есть, если для любых двух точек x1 и x2, где x1 < x2, значение функции f(x1) будет меньше значения функции f(x2), то функция является возрастающей.
Как можно определить, что функция возрастает?
Для определения возрастания функции нужно сравнить значения функции в двух разных точках. Если для любых двух точек x1 и x2, где x1 < x2, значение функции f(x1) будет меньше значения функции f(x2), то функция является возрастающей.
Какие примеры возрастающих функций можно привести?
Примеры возрастающих функций включают линейную функцию y = kx + b, где k > 0, экспоненциальную функцию y = a^x, где a > 1, и много других. Возрастание может быть представлено различными типами функций.
Каким образом возрастание функции отличается от убывания?
Возрастание функции означает, что ее значения увеличиваются по мере увеличения аргумента, тогда как убывание функции означает, что ее значения уменьшаются по мере увеличения аргумента. То есть, при возрастании функции значение f(x1) будет меньше значения f(x2), если x1 < x2, а при убывании — больше.
Какое значение имеет возрастание функции в математике?
Возрастание функции является важным понятием в математике, так как позволяет анализировать поведение функции и находить ее экстремумы, определять интервалы монотонности и другие характеристики функции. Оно также может иметь практическое применение в решении задач различных областей, таких как физика, экономика и т. д.
Что такое возрастание в математике?
Возрастание в математике – это свойство функции, при котором значение функции возрастает с увеличением аргумента. Другими словами, если для любых двух значений аргумента x1 и x2, при условии x1 < x2, значение функции f(x1) меньше значения функции f(x2), то функция называется возрастающей.




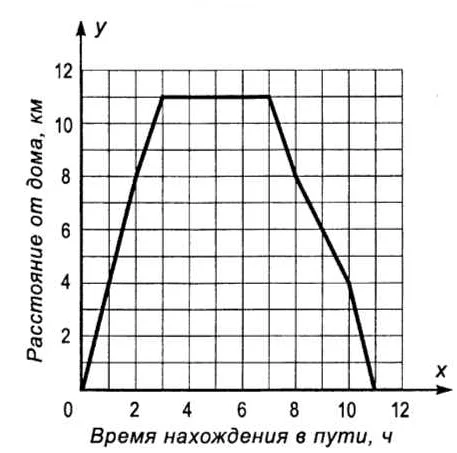
Возрастание в математике — это увеличение значения функции или числа с увеличением независимой переменной. Это понятие широко применяется в различных областях математики, физики и экономики. Например, если рассматривать функцию, описывающую движение тела, и время является независимой переменной, то увеличение времени будет приводить к увеличению позиции тела. Также возрастание может быть представлено в виде графика, где ось абсцисс отражает независимую переменную, а ось ординат — значение функции. При возрастании график будет стремиться вверх. Возрастание — одно из основных понятий математики, позволяющее анализировать и описывать различные процессы и явления.
Отличная статья! Наконец-то я понял, что такое возрастание в математике. Спасибо автору за простое и понятное объяснение. Теперь я знаю, что функция возрастает, если значение функции увеличивается при увеличении аргумента. Это очень важно в решении различных задач и построении графиков. Например, функция y = x^2 возрастает на всей числовой прямой, так как при увеличении x увеличивается и значение функции. Теперь я могу легко определить, возрастает ли функция или нет. Спасибо за познавательную статью!
Очень интересная статья! Всегда было любопытно узнать, что такое возрастание в математике. Благодаря данной статье я понял, что это рост или увеличение значений функции при увеличении аргумента. Примеры, представленные в статье, действительно помогли мне лучше понять эту концепцию. Например, график возрастающей функции, который постепенно поднимается вверх, или пример с возрастанием температуры с каждым днем. Это применение возрастания в реальной жизни дает мне уверенность в том, что эта тема имеет практическую ценность. Большое спасибо автору за ясное объяснение и интересные примеры!
Возрастание в математике — это понятие, которое означает, что последовательность чисел или функция увеличивается по мере увеличения аргумента. То есть, каждый следующий элемент или значение функции больше предыдущего. Это важное понятие в арифметике и анализе, которое помогает нам анализировать и понимать различные математические модели и явления. Примером возрастания может служить последовательность натуральных чисел: 1, 2, 3, 4 и так далее. Каждое следующее число в этой последовательности больше предыдущего. Также функция y = x^2 является примером возрастающей функции. При увеличении значения аргумента x, значение функции y также увеличивается. Возрастание в математике имеет важное значение не только в теории чисел, но и в различных областях науки и техники. Это понятие помогает нам анализировать и предсказывать различные математические модели и явления в реальном мире. Поэтому понимание возрастания является важным для всех, кто интересуется математикой и ее приложениями.
Математика — это наука, которая изучает законы и свойства чисел, формул и уравнений. Одним из важных понятий в математике является возрастание. Возрастание — это процесс увеличения значений функции или числовой последовательности по мере увеличения аргумента или номера элемента последовательности. Возрастание можно представить как движение вперед, увеличение чисел на числовой оси или графике функции. Например, если у нас есть функция f(x), и для каждого увеличения значения x, значение f(x) также увеличивается, то мы можем сказать, что функция возрастает. Примером возрастания может служить простая арифметическая последовательность, где каждый следующий член больше предыдущего. Например, рассмотрим последовательность чисел: 1, 3, 5, 7, 9. Здесь каждый следующий член увеличивается на 2, и мы видим, что последовательность возрастает. Возрастание имеет много практических применений в различных областях, включая финансы, экономику, физику и т. д. Понимание этого понятия помогает нам анализировать и прогнозировать данные, строить графики и решать различные задачи. Таким образом, возрастание в математике — это процесс увеличения значений функции или последовательности по мере увеличения аргумента или номера элемента. Это концепция, которая играет важную роль в понимании и использовании математических моделей и решении различных задач.