Графики в математике 6 класс: определение, функции и примеры

В статье вы узнаете, что такое графики в математике для учеников 6 класса. Рассмотрены основные понятия: координатная плоскость, оси координат, построение графиков и их анализ. Описание простых примеров и упражнений помогут легко понять эту тему и успешно решать задачи.

График – это графическое представление математического объекта. Он позволяет визуализировать зависимость одной величины от другой. Графики широко используются в математике, физике, экономике и многих других науках. Графики в математике 6 класса – это одна из основных тем, которую изучают школьники на уроках.

Изучение темы «Графики в математике 6 класса» позволяет ученикам научиться строить графики линейных функций, определять их смысловой смысл и решать задачи, связанные с графиками. Одним из главных преимуществ графиков является возможность увидеть закономерности и зависимости между величинами, что в свою очередь помогает принимать правильные решения и находить оптимальные решения проблем.

В данной статье мы рассмотрим основные понятия, примеры, задачи и решения связанные с графиками в математике 6 класса. Кроме того, мы предоставим полезные советы и инструкции, которые помогут ученикам более глубоко усвоить эту важную для математики тему.

Что такое график?

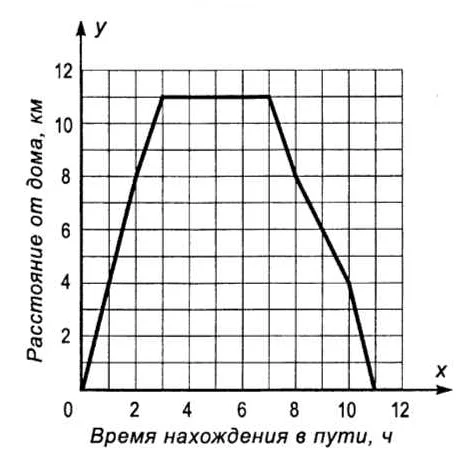
График – это изображение зависимости одной величины от другой. Обычно, на графике отображаются значения функции в зависимости от изменяющегося аргумента. В математике, график является отражением различных функций и уравнений, позволяющих подробно изучить их свойства. В графическом виде, искомые величины наглядно представлены на координатной плоскости.

Например, график функции y = 2x + 1 – это множество точек на плоскости, где координаты y определяются по формуле y = 2x + 1.

Графики также используются для решения задач различной сложности. На графиках можно определить, где значение функции равно 0, максимально или минимально. Они позволяют точно определить точки пересечения графиков разных функций, а также установить, имеет ли функция решения и какие они будут.

Координатная плоскость – это графический способ представления системы координат, в котором горизонтальная ось (x) пересекается с вертикальной осью (y) в одной точке, называемой началом координат. Размещение и размеры графика (или графиков) определяются на основании значений переменных и их возможного изменения. Координатная плоскость представляет двумерную систему координат, где оси каждая из которых представлены числами, и их цифры можно указывать на диаграмме.

Например, на графике функции y = f(x) значения на оси x могут изменяться от -5 до 5, а значения на оси y могут изменяться от -10 до 10.

Графики прямых и функций

График прямой — это геометрическая фигура, представляющая отрезок, на котором лежат все её точки. Коэффициенты уравнения такой прямой могут иметь значения любых чисел и определяют её угловой коэффициент и точку, через которую она проходит.

Функция представляет собой зависимость между двумя переменными — аргументом и значением. График функции — это множество точек (x, y), где x — значение аргумента, а y — значение функции. График функции может быть представлен кривой или несколькими линиями, в зависимости от формулы функции и её типа.

Чтобы построить графики прямых и функций, можно использовать координатную плоскость — систему двух пересекающихся прямых, называемых осями координат. Горизонтальная ось называется осью абсцисс, а вертикальная ось называется осью ординат.

Один из способов построения графика — задать несколько значений для аргумента и рассчитать соответствующие значения функции, затем отметить точки на координатной плоскости и соединить их линией. Таким образом, можно построить график функции.

• Графиком линейной функции y=kx+b является прямая, проходящая через точку (0, b) и с угловым коэффициентом k.
• График квадратичной функции y=ax^2+bx+c является параболой с вершиной в точке (-b/2a, f(-b/2a)), где f(-b/2a) — значение функции в данной точке.

Зная основные особенности графиков прямых и функций, можно решать задачи на их построение и анализ. Например, требуется найти точки пересечения двух прямых или определить область значений функции. Для этого нужно использовать знания о свойствах и формулах прямых и функций, а также умение работать с координатной плоскостью.

Примеры построения графиков

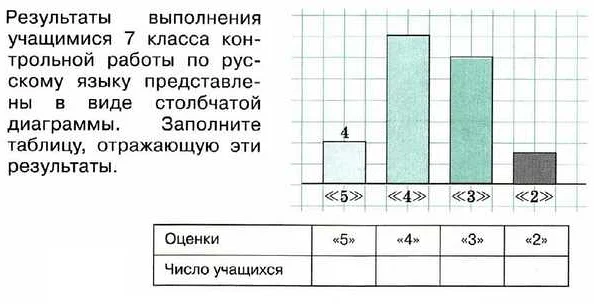
1. График прямой линии:

Прямую линию можно построить по двум точкам, через которые она проходит. Например, если у нас есть точки (3,5) и (7,9), то прямую линию можно нарисовать следующим образом:

ХY

3	5
7	9

Для построения графика необходимо провести прямую линию через эти точки.

2. График параболы:

Параболу можно построить по ее уравнению вида y = ax^2 + bx + c. Например, если у нас есть уравнение y = 2x^2 + 3x + 1, то можно построить график следующим образом:

1. Найти координаты вершины параболы: x = -b/2a, y = c — b^2/4a;
2. Найти хотя бы две точки на параболе, например, подставив x = 0 и x = 1;
3. Построить график, используя найденные точки и вершину параболы.

3. График функции, заданной таблицей:

Если функция задана таблицей значений x и y, то можно построить график, разместив точки на координатной плоскости и соединив их линиями. Например:

ХY

1	-2
2	1
3	4
4	5
5	6

Для построения графика необходимо провести линию по точкам, соответствующим значениям x и y в таблице.

Формулы функций и их графики

Функция – это соответствие между входным и выходным значениями, то есть, каждому входному значению функция ставит в соответствие определенное выходное значение. Функции могут быть заданы формулами, которые позволяют получить выходное значение для любого входного значения. Формулы функций могут быть выражены с помощью алгебраических операций, тригонометрических функций и других элементарных функций.

График функции – это геометрическое представление функции на плоскости. График функции представляет собой множество точек, координаты которых соответствуют входным и выходным значениям функции. Графики функций могут быть использованы для анализа и визуализации свойств функций.

Примером функции может служить, например, функция y = 2x + 3, которая задается следующей формулой: y = f(x) = 2x + 3. В данном случае, функция принимает на вход число x, умножает его на 2, прибавляет 3 и возвращает результат – число y. График этой функции будет представлен прямой линией на плоскости с координатной осью x и y.

Другим примером функции может быть квадратная функция y = x^2, которая задается следующей формулой: y = f(x) = x^2. В данном случае, функция принимает на вход число x, возводит его в квадрат и возвращает результат – число y. График этой функции будет представлен параболой на плоскости с координатной осью x и y.

• При анализе графиков функций, важно обратить внимание на следующие характеристики:
  • Область определения функции.
  • Область значений функции.
  • Нули функции и их местоположение на графике.
  • Экстремумы функции и их местоположение на графике.
  • Монотонность функции и ее изменение на интервалах.

Линейные функции

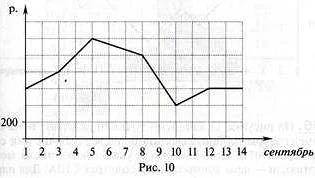
Линейные функции являются одними из основных объектов изучения в математике. Линейной функцией называется функция, график которой является прямой линией на плоскости. Она задаётся уравнением вида y = kx + b, где k и b — это некоторые константы.

Коэффициент k называется наклоном или скоростью изменения функции. Если k > 0, то функция возрастает, если k < 0, то функция убывает. Коэффициент b называется свободным членом. Он определяет точку пересечения графика функции с осью OY. Если b > 0, то точка пересечения находится выше оси OX, если b < 0 — то ниже.

Пример линейной функции: y = 2x — 3. Наклон функции равен 2, что означает, что при каждом увеличении x на 1, y увеличится на 2. Свободный член равен -3, что означает, что график функции пересечет ось OY на точке (0, -3).

Чтобы построить график линейной функции, нужно выбрать несколько значений для x, вычислить соответствующие значения y и отметить полученные точки на плоскости. Затем соединить точки прямой линией.

Линейные функции широко используются в реальной жизни для моделирования взаимосвязей и прогнозирования результатов. Например, график функции y = 2x — 3 может использоваться для определения стоимости товара в зависимости от его количества.

Квадратичные функции

Квадратичные функции являются одним из типов функций в математике. Такой тип функций имеет вид f(x) = ax^2 + bx + c, где a, b и c – числовые коэффициенты. Квадратичные функции образуют график параболы, которая может быть направленной вверх или вниз, в зависимости от коэффициента a. Если коэффициент a положительный, то парабола направлена вверх, если же отрицательный, то парабола направлена вниз.

Квадратичные функции часто используются для анализа и прогнозирования данных. Например, они могут быть использованы для анализа бизнес-процессов и прогнозирования продаж. Также, квадратичные функции могут использоваться для определения максимального и минимального значения функции, то есть точки экстремума. Это может быть полезным, например, при решении задач, связанных с максимальным и минимальным производством.

Для создания графика квадратичной функции можно использовать таблицу значений или компьютерную программу, в которой можно задать коэффициенты a, b и c и построить график с помощью функции-графикатора. Для решения задач, связанных с квадратичными функциями, необходимо уметь находить корни уравнения или точки пересечения графика с осями координат, экстремумы функции и диапазоны значений функции. Эти навыки можно приобрести путем решения практических задач и практики построения графиков функций.

• Пример задачи на квадратичные функции: найти корни уравнения f(x)=3x^2-5x+2.
• Решение: для нахождения корней уравнения необходимо решить уравнение f(x)=0. Обозначим D=b^2-4ac и вычислим его значение: D=(−5)^2−4 · 3 · 2 = 1. Значит, у уравнения есть два корня: x1=(5+1)/6 и x2=(5-1)/6.

Построение графиков линейных и квадратичных функций

График функции – это иллюстрация того, каким образом значения функции изменяются в зависимости от ее аргумента. Для построения графиков линейных и квадратичных функций можно использовать различные методы.

Линейная функция:

Линейная функция задается формулой y = kx + b, где k и b – коэффициенты функции. Для построения ее графика необходимо задать несколько точек и провести прямую, проходящую через них. Например, для функции y = 2x + 1 можно выбрать точки (-1,-1), (0,1) и (1,3). Присвоив каждой из них значение x и подставив в формулу функции, получим значения y координат соответствующих точек. Значения координат заносим в таблицу и, соединив точки прямой линией, получаем график функции.

Квадратичная функция:

Квадратичная функция имеет формулу y = ax^2 + bx + c, где a, b и c – коэффициенты функции. Для построения ее графика также необходимо задать несколько точек, однако, в отличие от линейной функции, количество точек должно быть не меньше трех. Если количество точек меньше трех, то построить график невозможно. После определения координат точек необходимо построить график квадратичной функции, используя метод предыдущего пункта или же наложив график на оси координат, где значение x будет увеличиваться слева направо отрицательно, а справа направо положительно, а значение y – вертикально посередине. Для построения графика квадратичной функции также можно использовать таблицу значений.

Построение графиков линейных и квадратичных функций – это важный и практический навык, который поможет в решении задач и понимании процессов, происходящих в различных ситуациях.

Задачи на нахождение координат точки на графике

Одна из важнейших задач на графике в математике 6 класса – это задачи на нахождение координат точки на графике.

Координаты точки на графике задаются парой чисел (x,y), где x – это координата точки по оси абсцисс, а y – координата точки по оси ординат. Координаты точки могут быть определены с помощью графика, уравнения прямой или функции.

Пример задачи на нахождение координат точки на графике: на плоскости дан график функции f(x) = x + 2. Найти координаты точки, которая находится на расстоянии 5 от оси ординат и на расстоянии 3 от оси абсцисс.

Решение: так как точка находится на расстоянии 5 от оси ординат, значит её координата по оси абсцисс равна 5. Аналогично, её координата по оси ординат равна 3. Таким образом, координаты искомой точки равны (5,3).

Другой пример задачи: на графике прямой y = 2x – 1 отмечены две точки: A(2,3) и B(3,5). Найти координаты точки С, лежащей на данной прямой и находящейся между точками A и B.

Решение: нам нужно найти координаты точки на прямой, которая лежит между точками A и B. Сначала найдем уравнение прямой, проходящей через точки A и B:

к = (y2 – y1)/(x2 – x1) = (5 – 3)/(3 – 2) = 2.

Затем найдем свободный коэффициент:

b = y1 – kx1 = 3 – 2*2 = -1.

Таким образом, уравнение прямой, проходящей через точки A и B, имеет вид y = 2x – 1. Теперь найдем координаты точки С: будем искать её координаты в виде (х,у). Так как точка лежит между точками А и В, её координаты должны удовлетворять условию 2x – y = -1. Подставляем x = 2.5 (середина отрезка AB) и находим у:

y = 2*2.5 – (-1) = 6.

Координаты точки С равны (2.5,6).

Таким образом, задачи на нахождение координат точки на графике в математике 6 класса могут быть различной сложности, но при определенных знаниях и умении решать уравнения и системы уравнений, они становятся несложными.

Решения задач на построение графиков функций

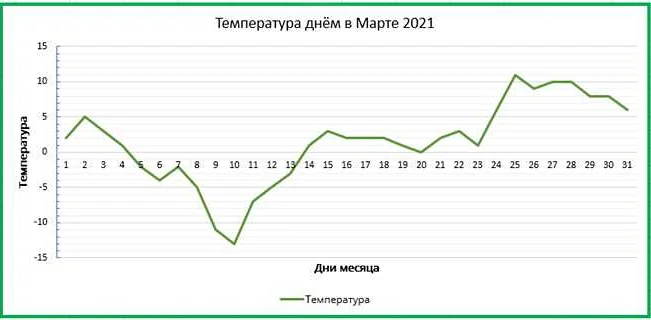
Для решения задач на построение графиков функций необходимо учитывать следующие моменты:

• Значения функции для нескольких точек должны быть известны;
• Необходимо определить, где кривая функции пересекает оси координат, её асимптоты, максимальные и минимальные значения;
• Необходимо учитывать значения функции, которые определяются графически.

Для построения графика функции возможно использовать таблицу значений функции. Она представляет собой таблицу, в которой указываются значения аргументов и соответствующих им значений функции.

Также можно использовать графический метод – построение графика функции на координатной плоскости. Это позволяет более наглядно представить поведение функции на всей области определения.

Для построения графика функции на плоскости существует ряд правил:

1. Построение прямой точками. Значения функции полученные из таблицы новыми точками.
2. Необходимо выполнять стандартные действия при построении графиков, такие как: пересчет масштаба, построение осей координат, отложение точек на осях координат.
3. На оси абсцисс откладывают значения аргумента, на оси ординат – соответствующие значения функции.
4. Для построения графика функции рекомендуется ставить точки на разных расстояниях по оси x.

После построения графика функции соответствующим образом необходимо анализировать поведение функции и определять ее свойства.

Видео по теме:

Вопрос-ответ:

Что такое график функции?

График функции – это точки на координатной плоскости (двумерном пространстве), где значение x соответствует аргументу функции, а значение y – ее значению. Более простыми словами, это изображение функции на плоскости.

Каким образом можно построить график функции?

Для построения графика функции нужно: 1) определить область определения функции; 2) составить таблицу значений функции; 3) построить координатную плоскость с помощью системы координат; 4) отметить точки, соответствующие значениям функции на плоскости; 5) соединить точки линией.

Какие функции можно представить в виде графиков?

В виде графиков можно представить самые разные функции: линейные, квадратичные, степенные, тригонометрические, логарифмические, экспонентные и т.д.

Для чего нужны графики в математике?

Графики позволяют наглядно представить и проанализировать свойства и характеристики функций, изучать их поведение на протяжении всей области определения, а также решать уравнения и неравенства на их основе. Графики очень важны в математике и в ряде других наук.

Как решать задачи на графики в 6 классе?

Для решения задач на графики нужно внимательно прочитать условие, точно определить, какая функция задана, построить ее график, отметить на нем нужную точку или отрезок и проанализировать данные, чтобы дать правильный ответ.

Как найти коэффициент наклона прямой по ее графику?

Для того чтобы найти коэффициент наклона прямой, нужно определить разность между y-координатами двух точек на прямой. Затем нужно определить разность между x-координатами этих же точек. Отношение первой разности ко второй будет являться коэффициентом наклона прямой.

Как построить график функции, если ее уравнение представлено в виде y = kx + b?

Для построения графика функции y = kx + b нужно знать, что коэффициент k определяет угол наклона прямой, а коэффициент b – точку пересечения с осью y. Начиная с точки (0, b), нужно отложить от нее по оси x одинаковые отрезки и соединить полученные точки линией с углом наклона k.

Примеры задач на использование графиков в решении задач

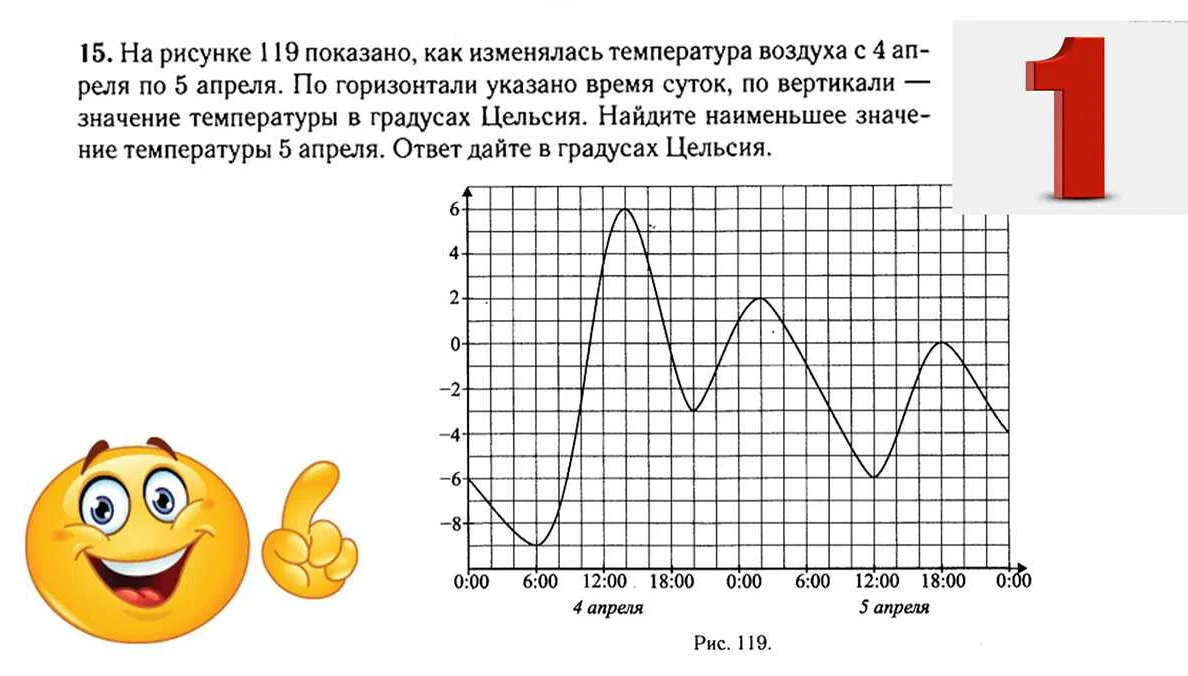
Задача 1: На графике изображена зависимость цены на компьютеры от времени. Найдите цену компьютера через 3 года, если на момент начала отсчета его цена была 30 000 рублей.

Решение: Для определения цены компьютера через 3 года, необходимо найти точку на графике, которая соответствует данному временному промежутку. Проведем вертикальную линию от точки начала отсчета времени до точки, которая находится на расстоянии 3 единицы по оси времени (горизонтальной оси). Проведем горизонтальную линию от полученной точки до графика, чтобы определить цену компьютера. По графику видно, что цена на компьютер через 3 года составит 40 000 рублей.

Задача 2: На графике изображена зависимость скорости движения автомобиля от времени. Найдите максимальную скорость автомобиля и время, когда она была достигнута.

Решение: Для определения максимальной скорости автомобиля необходимо найти точку на графике с наибольшим значением скорости. По графику видно, что максимальная скорость автомобиля достигнута на отрезке между 6 и 7 секундами и составляет 80 км/ч. Для определения времени, когда была достигнута максимальная скорость, необходимо провести вертикальную линию от точки максимальной скорости до оси времени и определить соответствующее значение времени. По графику видно, что максимальная скорость была достигнута через 6,5 секунды.

Задача 3: На графике изображена зависимость количества просмотренных фильмов в кинотеатре от дня недели. Определите день недели, когда посещаемость кинотеатра была максимальной, и количество просмотренных фильмов в этот день.

Решение: Для определения дня недели с максимальной посещаемостью кинотеатра, необходимо найти точку на графике с наибольшим значением количества просмотров. По графику видно, что максимальное количество просмотров достигнуто в воскресенье и составляет 1200. Для определения количества просмотренных фильмов в этот день необходимо провести горизонтальную линию от полученной точки до оси, на которой отмечены значения количества просмотренных фильмов. По графику видно, что в воскресенье было просмотрено 8 фильмов.

Задача 4: На графике изображена зависимость массы тела от роста. Определите индекс массы тела (ИМТ) человека с ростом 170 см и массой 70 кг и укажите, в какую категорию входит его ИМТ.

Решение: Для определения ИМТ человека необходимо воспользоваться формулой ИМТ=масса/рост^2, где масса указана в килограммах, а рост в метрах. В данной задаче рост указан в сантиметрах, поэтому его необходимо привести к метрам. Для этого рост нужно разделить на 100. После этого можно подставить значения массы и роста в формулу ИМТ и получить результат: ИМТ=24,2. По таблице нормального веса для ИМТ можно определить категорию, к которой относится человек с таким ИМТ. В данном случае ИМТ соответствует нормальному весу.

Справочник формул и определений для работы с графиками

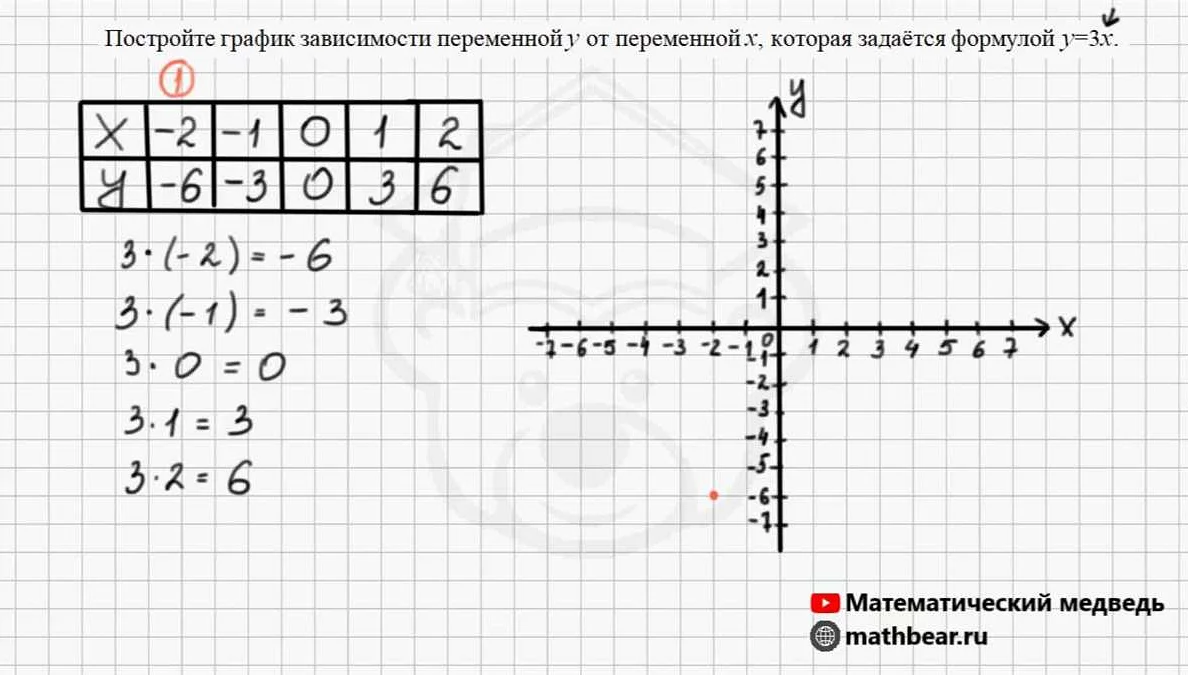
График – это изображение зависимости одной величины от другой на плоскости или в пространстве.

Координатные оси – это две перпендикулярные прямые, которые используются для построения графиков на плоскости. Они называются осью абсцисс (горизонтальная) и осью ординат (вертикальная).

Уравнение прямой – это уравнение вида y = kx + b, где k – это коэффициент, который определяет наклон прямой, b – это свободный член, который определяет точку пересечения прямой с осью ординат.

Коэффициент наклона – это число, которое определяет угол наклона прямой относительно оси абсцисс.

Точка пересечения с осью ординат – это точка на прямой, которая пересекает ось ординат.

Пересечение двух прямых – это точка, в которой две прямые пересекаются на плоскости. Эта точка является решением системы уравнений, задающих эти прямые.

Коэффициенты функции – это числа, которые используются для определения функции на графике. Они могут включать параметры, такие как угол наклона или точки пересечения.

Графическое решение системы уравнений – это метод решения систем уравнений, при котором ищутся графические представления уравнений и их пересечений на плоскости.

Вычисление коэффициентов – это процесс нахождения значений коэффициентов, которые определяют наклон прямой, ее точку пересечения с осью ординат и т.д.