Что такое выражение к задаче по математике
Содержимое
- 1 Что такое выражение к задаче по математике
- 1.1 Понятие выражение к задаче по математике
- 1.2 Определение выражение к задаче
- 1.3 Цель и назначение выражения к задаче
- 1.4 Примеры выражений к задаче
- 1.5 Основные элементы выражения к задаче
- 1.6 Роль выражения к задаче в решении математических задач
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое выражение к задаче по математике?
- 1.8.0.2 Какие операции могут быть использованы в выражении к задаче по математике?
- 1.8.0.3 Какие примеры выражений можно привести?
- 1.8.0.4 Каким образом выражение помогает решить задачу?
- 1.8.0.5 Как выбрать правильное выражение для задачи?
- 1.8.0.6 Какие основные понятия входят в определение выражения к задаче по математике?
- 1.9 Особенности составления выражения к задаче
- 1.10 Практическое применение выражений к задачам по математике
Выражение к задаче по математике — это математическое выражение, которое используется для решения конкретной задачи. Оно может содержать числа, переменные, операции и другие математические символы. Понимание выражения к задаче помогает студентам анализировать и решать различные задачи, связанные с математикой.
В мире математики выражение к задаче играет важную роль. Оно позволяет сформулировать математическую задачу в языке алгебры и логики. Выражение представляет собой комбинацию чисел, переменных, операторов и функций, которые позволяют производить различные вычисления.
Выражение к задаче может быть простым или сложным, в зависимости от количества и сложности используемых элементов. Простые выражения содержат только одно действие или операцию, например, сложение двух чисел. Сложные выражения могут включать несколько операций, переменных и функций, например, выражение для вычисления значения функции в зависимости от нескольких переменных.
Операторы в выражении к задаче определяют, какие математические операции нужно выполнить. Существуют различные операторы, такие как сложение, вычитание, умножение и деление, а также операторы для работы с функциями, логическими значениями и другими математическими объектами.
Пример: Выражение «2 + 3» представляет собой простое выражение, которое означает сложение чисел 2 и 3. Результатом этого выражения является число 5.
Понимание выражения к задаче помогает математикам анализировать и решать различные задачи, а также использовать математику для моделирования реальных ситуаций и прогнозирования результатов.
Понятие выражение к задаче по математике
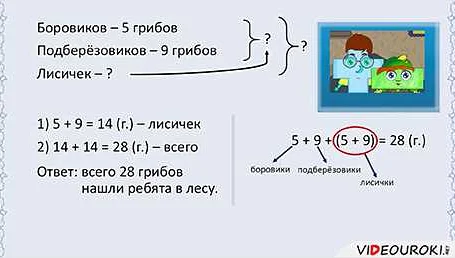
В задачах по математике выражение часто используется для описания условий задачи или для вычисления требуемого результата. Оно может включать операции сложения, вычитания, умножения, деления, возведения в степень и другие математические операции.
Примеры выражений в задачах по математике:
- Если переменная x равна 5, то выражение 2x + 3 будет равно 13.
- Для вычисления площади прямоугольника со сторонами a и b используется выражение a * b.
- Выражение 3n — 2 представляет собой численное значение при заданном значении переменной n.
Выражение к задаче по математике позволяет формализовать и решить математическую задачу, используя язык математики и алгоритмы вычислений.
Определение выражение к задаче

Выражение к задаче в математике представляет собой математическое выражение или формулу, используемую для решения конкретной задачи или вычисления значения неизвестной величины.
Выражение может содержать числа, операторы (сложение, вычитание, умножение, деление), переменные и скобки. В зависимости от задачи, выражение может также включать функции, степени, корни и другие математические операции.
Выражения к задачам могут быть простыми или сложными, их формат и структура зависят от поставленной задачи. Например, для задачи взятия производной функции может использоваться выражение вида f'(x) = lim(h→0) (f(x+h) — f(x))/h, где f(x) — функция, а x — переменная.
Выражение к задаче является важной частью решения математической задачи, так как позволяет сформулировать алгоритм для получения нужного результата. Выражение может быть записано в аналитической или символической форме, в зависимости от требований задачи или метода решения.
Цель и назначение выражения к задаче

Выражение к задаче представляет собой математическую формулу или уравнение, которое описывает связь между различными величинами и операциями, происходящими в задаче. Оно позволяет перевести словесное условие задачи в язык математики, что упрощает анализ и решение задачи.
Выражение к задаче может включать в себя различные математические операции, такие как сложение, вычитание, умножение и деление, а также степени, корни, функции и т. д. Оно может также содержать переменные, которые представляют неизвестные величины, которые нужно найти.
Примеры выражений к задаче в математике:
- Выражение для нахождения площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
- Выражение для нахождения объема цилиндра: V = π * r^2 * h, где r — радиус основания цилиндра, h — высота цилиндра.
- Выражение для нахождения процента: процент = (часть / целое) * 100%.
Таким образом, выражение к задаче является важным инструментом в математике, который помогает перевести словесное условие задачи в язык символов и операций математики, упрощая ее решение и анализ.
Примеры выражений к задаче
Ниже приведены примеры выражений, которые могут использоваться при решении математических задач:
- Выражение для вычисления площади прямоугольника: площадь = длина * ширина
- Выражение для нахождения суммы двух чисел: сумма = число1 + число2
- Выражение для вычисления периметра круга: периметр = 2 * π * радиус
- Выражение для нахождения среднего арифметического двух чисел: среднее = (число1 + число2) / 2
Это лишь небольшой перечень примеров выражений, которые могут быть использованы при решении математических задач. В каждом конкретном случае необходимо анализировать условие задачи и выбирать соответствующее выражение для нахождения решения.
Основные элементы выражения к задаче
Выражение к задаче в математике представляет собой математическое выражение, которое используется для решения задачи или вычисления значений.
Основными элементами выражения к задаче являются:
ЭлементОписаниеПример
| Числа | Цифры или числовые значения, которые используются в выражении. | 3, 5.5, -2 |
| Операторы | Символы или знаки, которые указывают на выполняемые действия над числами. | +, -, *, / |
| Переменные | Символы или буквы, которые представляют неизвестные значения или величины. | x, y, z |
| Скобки | Символы, используемые для группировки элементов выражения и определения порядка выполнения операций. | (, ) |
Например, в выражении «2 + x — 3 * (y + 1)» числа «2» и «3» являются числами, операторы «+», «-» и «*» указывают на выполнение сложения, вычитания и умножения, переменные «x» и «y» представляют неизвестные значения, а скобки «(«, «)» используются для группировки элементов выражения.
Роль выражения к задаче в решении математических задач

Решение математической задачи начинается с формулировки выражения к задаче. Это позволяет перевести условие задачи из естественного языка в язык математики и представить его в виде уравнения или неравенства.
Выражение к задаче играет ключевую роль в решении математических задач, так как оно позволяет:
- Определить неизвестные величины, которые нужно найти. В выражении к задаче неизвестные обозначаются буквами, например, x или y.
- Соотнести информацию из условия задачи с математическими операциями. Выражение к задаче позволяет определить, какие операции нужно выполнить с известными величинами, чтобы найти неизвестные.
- Решить уравнение или неравенство, получившееся в результате формулировки выражения к задаче. Решение уравнения или неравенства дает значения неизвестных величин, которые являются ответами на задачу.
- Проверить полученные ответы на соответствие условию задачи. Подстановка найденных значений в выражение к задаче и его проверка позволяют убедиться, что ответы являются верными.
Например, если задача состоит в нахождении площади прямоугольника, выражение к задаче может быть следующим: S = a * b, где S — площадь, а и b — стороны прямоугольника.
Таким образом, выражение к задаче является неотъемлемой частью решения математической задачи. Оно позволяет перевести условие задачи в язык математики, определить неизвестные величины и выполнить необходимые математические операции для нахождения решения.
Видео по теме:
Вопрос-ответ:
Что такое выражение к задаче по математике?
Выражение в задачах по математике представляет собой математическое выражение, состоящее из чисел, переменных и операций. Оно используется для описания задачи и формулировки условия.
Какие операции могут быть использованы в выражении к задаче по математике?
В выражении к задаче по математике могут использоваться различные операции, такие как сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Также могут присутствовать скобки для изменения порядка выполнения операций.
Какие примеры выражений можно привести?
Примерами выражений к задаче по математике могут быть: «Сумма двух чисел», «Произведение трех чисел», «Разность числа и его удвоения». Это только некоторые из возможных примеров, так как выражения могут быть очень разнообразными.
Каким образом выражение помогает решить задачу?
Выражение помогает решить задачу, так как оно позволяет сформулировать условие задачи в математической форме и выразить необходимые величины и операции. С помощью выражения можно проводить вычисления и получить конкретные числовые значения или алгебраические уравнения, которые позволяют найти решение задачи.
Как выбрать правильное выражение для задачи?
Для выбора правильного выражения для задачи необходимо внимательно прочитать условие задачи и выделить ключевые слова и фразы, которые указывают на требуемые математические операции. Затем можно использовать эти ключевые слова для составления выражения. Если необходимо, можно использовать переменные для обозначения неизвестных величин.
Какие основные понятия входят в определение выражения к задаче по математике?
Выражение к задаче по математике представляет собой математическое выражение или формулу, которая содержит числа, переменные и операции. Оно используется для описания и решения математических задач. В выражение могут входить такие понятия, как сумма, разность, произведение, частное, степень и корень.
Особенности составления выражения к задаче

Выражение к задаче в математике представляет собой математическое выражение, которое используется для решения поставленной задачи. При составлении выражения необходимо учитывать несколько особенностей.
1. Правильное формулирование задачи: Выражение должно точно отражать условие задачи и ее требования. Необходимо внимательно проанализировать задачу и понять, какие величины и операции в ней задействованы.
2. Использование переменных: Выражение может содержать переменные, которые представляют неизвестные величины. При этом необходимо выбрать подходящие обозначения для переменных и определить их смысл в контексте задачи.
3. Выбор операций: В зависимости от постановки задачи, в выражении могут использоваться различные математические операции, такие как сложение, вычитание, умножение, деление, возведение в степень и другие. Необходимо выбрать соответствующие операции для правильного решения задачи.
4. Порядок действий: При составлении выражения нужно учитывать порядок выполнения операций. Для этого можно использовать скобки или определенные правила приоритета операций. Это позволит избежать ошибок и получить правильный результат.
5. Проверка корректности выражения: После составления выражения необходимо проверить его корректность и соответствие условию задачи. Для этого можно привести примеры числовых значений переменных и вычислить значение выражения, чтобы убедиться в его правильности.
ПримерВыражениеРезультат
| Задача о площади прямоугольника | Площадь = Длина × Ширина | Площадь прямоугольника |
| Задача о скорости движения автомобиля | Скорость = Расстояние ÷ Время | Скорость автомобиля |
Практическое применение выражений к задачам по математике
Практическое применение выражений к задачам по математике может быть найдено во множестве областей. Например, в экономике и финансах они используются для моделирования бюджетов и финансовых потоков. В физике и инженерии они помогают описывать различные физические явления и процессы. В компьютерных науках они используются для создания алгоритмов и программирования. В статистике они позволяют анализировать данные и делать выводы.
Применение выражений в решении задач по математике позволяет структурировать информацию и проводить логические рассуждения. Они позволяют сформулировать математическую модель задачи и преобразовать ее в систему уравнений или неравенств. Затем, используя методы алгебры или анализа, можно найти решение и получить ответ на поставленную задачу.
Примеры практического применения выражений к задачам по математике включают решение задач на определение неизвестных величин, вычисление площадей и объемов, построение графиков функций, нахождение экстремумов и корней уравнений, анализ статистических данных и т.д.
Все эти примеры демонстрируют, что выражения являются необходимым инструментом в решении задач по математике. Они позволяют представить сложные математические операции в удобной форме и провести анализ, что делает их использование эффективным и универсальным.
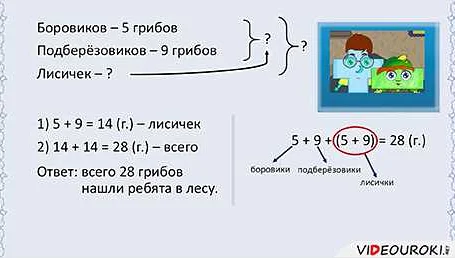




Статья очень понятно и доступно объяснила, что такое выражение к задаче по математике. Я считаю, что выражение — это математическое выражение или формула, которая используется для решения задачи. Оно может содержать числа, переменные, знаки операций и скобки. Примеры выражений, которые приведены в статье, помогли мне лучше понять, как они работают. Теперь я понимаю, что нужно уметь правильно сформулировать выражение, чтобы решить задачу. Статья очень полезна и помогла мне освоить эту тему. Большое спасибо автору!
Выражение к задаче по математике — это математическое выражение или формула, которая позволяет решить поставленную задачу. Оно состоит из чисел, переменных, операций и знаков, которые объединяются в определенном порядке. Выражение может быть использовано для вычисления значений, нахождения неизвестных величин или анализа различных математических моделей. Примером выражения к задаче может быть уравнение вида «2x + 3 = 7», где «x» — неизвестная величина. Решая это уравнение, можно найти значение «x», которое удовлетворяет условию задачи. Выражения к задачам по математике могут быть разными: от простых арифметических операций до сложных алгебраических или геометрических формул. Они используются в школьном курсе математики, а также в различных научных и инженерных областях. Важно понимать, что выражение к задаче является инструментом для решения математических задач и помогает систематизировать и анализировать информацию. Правильное построение и использование выражений позволяет получить точные и корректные результаты.