Что значит сравнить выражения в математике

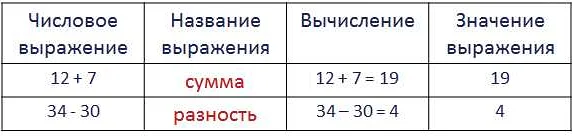
В математике сравнение выражений означает определение, какое из двух выражений больше или меньше другого. Сравнение может осуществляться с помощью знаков сравнения, таких как , ≤, ≥. Понимание процесса сравнения выражений важно для решения уравнений, неравенств и других математических задач.

Сравнение выражений является важной частью математического анализа и позволяет нам сравнивать различные математические выражения, чтобы определить их относительные значения. При сравнении выражений мы исследуем их свойства и отношения, чтобы понять, какое из них больше, меньше или равно другому выражению. Это позволяет нам принимать решения, делать выводы и решать задачи в различных областях науки и жизни.

Основные понятия, используемые при сравнении выражений, включают знаки сравнения, такие как «больше», «меньше» и «равно». Знак «>» используется для выражения «больше», знак »

Например, если у нас есть два выражения: 5 + 3 и 7, мы можем сравнить их, используя знаки сравнения. Выражение 5 + 3 будет равно 8, поэтому мы можем записать его как 8. Теперь мы можем сравнить 8 и 7, и у нас есть следующее выражение: 8 > 7. Это означает, что 8 больше, чем 7, и мы можем сделать вывод, что 5 + 3 больше, чем 7.

Сравнение выражений также позволяет нам устанавливать отношения между переменными и константами. Например, если у нас есть выражение x + 5 и выражение 10, мы можем использовать знаки сравнения, чтобы определить относительное значение x. Если мы придем к выводу, что x > 5, это означает, что x больше, чем 5, и мы можем использовать это знание для решения различных математических задач.

Определение и значение сравнения в математике

Операторы сравнения в математике позволяют утверждать, верно ли выражение или неравенство между двумя числами или переменными. Результатом сравнения является логическое значение «истина» или «ложь». Если сравнение истинно, то результат будет «истина», если сравнение ложно, то результат будет «ложь».

Для сравнения чисел используются следующие операторы:

• Оператор «равно» (==) — проверяет, равны ли значения двух выражений;
• Оператор «не равно» (!=) — проверяет, не равны ли значения двух выражений;
• Оператор «больше» (>) — проверяет, является ли значение первого выражения больше значения второго выражения;
• Оператор «меньше» (
• Оператор «больше или равно» (>=) — проверяет, является ли значение первого выражения больше или равным значению второго выражения;
• Оператор «меньше или равно» (

Сравнение в математике играет важную роль при решении различных задач и уравнений. Оно позволяет устанавливать отношения между числами и переменными, а также делать выводы на основе этих отношений.

Например, сравнение может быть использовано для определения, какое из двух чисел является большим или меньшим, для сортировки чисел по возрастанию или убыванию, для проверки условий в условных выражениях и циклах.

Выводы, сделанные на основе сравнения в математике, позволяют более точно описывать и анализировать различные явления и процессы в науке, технике, экономике и других областях знаний.

Видео по теме:

Что такое выражение в математике и как его сравнивают

Сравнение выражений в математике заключается в определении, равны ли они друг другу или какое из них больше или меньше. Для сравнения выражений используются различные математические свойства и правила, которые позволяют проводить операции с выражениями и получать ответы.

Когда сравнивают выражения, можно использовать следующие операции:

ОперацияЗначение

Равно (=)	Выражения равны друг другу, если они имеют одинаковое значение.
Не равно (≠)	Выражения не равны друг другу, если они имеют разное значение.
Больше (>)	Выражение слева больше, чем выражение справа, если его значение больше.
Меньше (	Выражение слева меньше, чем выражение справа, если его значение меньше.
Больше или равно (≥)	Выражение слева больше или равно выражению справа, если его значение больше или равно.
Меньше или равно (≤)	Выражение слева меньше или равно выражению справа, если его значение меньше или равно.

Сравнение выражений в математике играет важную роль в решении уравнений, нахождении корней и определении условий их существования. Правильное сравнение выражений позволяет упростить вычисления и получить точные результаты.

Роль знака сравнения в математических выражениях

В математике знак сравнения играет важную роль, позволяя нам сравнивать числа и выражения между собой.

Основные знаки сравнения в математике:

• Знак «меньше» (
• Знак «больше» (>)
• Знак «меньше или равно» (≤)
• Знак «больше или равно» (≥)
• Знак «равно» (=)
• Знак «не равно» (≠)

Знаки сравнения позволяют нам выражать отношения между числами. Например, с помощью знака «меньше» мы можем сказать, что одно число меньше другого.

Примеры:

• 2 < 5 — означает, что число 2 меньше числа 5
• 10 > 7 — означает, что число 10 больше числа 7
• 3 ≤ 3 — означает, что число 3 меньше или равно числу 3
• 8 ≥ 6 — означает, что число 8 больше или равно числу 6
• 4 = 4 — означает, что число 4 равно числу 4
• 9 ≠ 2 — означает, что число 9 не равно числу 2

Знаки сравнения используются в различных математических задачах и уравнениях для установления отношений между числами и переменными.

Вопрос-ответ:

Что значит сравнить выражения в математике?

Сравнение выражений в математике означает определение, какое из двух выражений больше, меньше или равно другому. Для этого используются различные математические символы, такие как знаки «>», »

Какие основные понятия используются при сравнении выражений в математике?

Основными понятиями при сравнении выражений в математике являются знаки сравнения и отношения. Знаки сравнения включают знаки «>», »

Как можно сравнить числа в математике?

Числа в математике можно сравнивать с помощью знаков сравнения «>», » 5 (8 больше 5). Если числа равны, мы можем использовать знак «=», например, 5 = 5 (5 равно 5).

Как можно сравнить переменные в математике?

Сравнение переменных в математике происходит по аналогии с сравнением чисел. Для этого используются знаки сравнения «>», » x (y больше x). Если переменные равны, мы можем использовать знак «=», например, x = y (x равно y).

Приведите примеры сравнения алгебраических выражений в математике.

В математике можно сравнивать алгебраические выражения, используя знаки сравнения «>», » 4x — 1 (2x + 3 больше 4x — 1) и 4x — 1 < 2x + 3 (4x — 1 меньше 2x + 3). Также, если алгебраические выражения равны, мы можем использовать знак «=», например, 2x + 3 = 4x — 1 (2x + 3 равно 4x — 1).

Какие основные понятия есть в математике для сравнения выражений?

Основные понятия в математике для сравнения выражений — это равенство и неравенство. Равенство означает, что два выражения имеют одинаковое значение. Неравенство указывает на то, что значения двух выражений различны и можно установить, какое из них больше или меньше.

Каким образом можно сравнить выражения в математике?

Сравнение выражений в математике возможно с помощью знаков сравнения. Знак равенства (=) используется для указания, что два выражения имеют одинаковое значение. Знаки неравенства (< и >) позволяют определить, какое из двух выражений больше или меньше. Кроме того, существуют знаки «меньше или равно» (≤) и «больше или равно» (≥), которые указывают на то, что значение одного выражения может быть равно или меньше (больше) значения другого выражения.

Основные типы сравнений в математике

Сравнение выражений может быть осуществлено с помощью различных математических операторов, таких как:

ОператорОбозначениеОписание

>	Больше	Оператор «больше» обозначает, что одно выражение или число больше другого.
	Меньше	Оператор «меньше» обозначает, что одно выражение или число меньше другого.
>=	Больше либо равно	Оператор «больше либо равно» обозначает, что одно выражение или число больше или равно другому.
	Меньше либо равно	Оператор «меньше либо равно» обозначает, что одно выражение или число меньше или равно другому.
=	Равно	Оператор «равно» обозначает, что два выражения или числа равны друг другу.
!=	Не равно	Оператор «не равно» обозначает, что два выражения или числа не равны друг другу.

Например, если имеются два числа a и b, то сравнение a > b будет истинно, если a больше b, и ложно в противном случае.

Сравнение в математике играет важную роль при решении уравнений, построении графиков и в других областях, где необходимо сравнивать значения и выражения.

Примеры сравнения чисел в математике

Сравнение чисел в математике играет важную роль при решении различных задач и установлении отношений между числами. Вот несколько примеров сравнения чисел:

Пример 1: Сравним числа 7 и 3. Знак «больше» (>) используется для выражения отношения, когда одно число больше другого. В данном случае, 7 > 3, что означает, что число 7 больше числа 3.

Пример 2: Сравним числа 5 и 5. Знак «равно» (=) используется, когда два числа имеют одинаковое значение. В данном случае, 5 = 5, что означает, что число 5 равно числу 5.

Пример 3: Сравним числа -2 и 0. Знак «меньше» (

Пример 4: Сравним числа -5 и -10. Знак «меньше» (

Пример 5: Сравним числа 1/2 и 1/4. Знак «больше» (>) также может использоваться для сравнения дробей. В данном случае, 1/2 > 1/4, что означает, что дробь 1/2 больше дроби 1/4.

Таким образом, сравнение чисел в математике позволяет определить отношения между числами и использовать эту информацию для решения задач и построения математических моделей.

Сравнение переменных и неизвестных в математических выражениях

Сравнение переменных и неизвестных может быть полезным для решения уравнений и неравенств, а также для анализа и сравнения различных математических моделей и функций.

Примеры сравнения переменных и неизвестных:

• Сравнение чисел: 2 < 5 (2 меньше 5), 7 > 3 (7 больше 3), 4 = 4 (4 равно 4).
• Сравнение переменных: x > y (x больше y), a < b (a меньше b), c = d (c равно d).
• Сравнение выражений: 2x + 3y < 10 (2x + 3y меньше 10), ax^2 + bx + c > 0 (ax^2 + bx + c больше 0).

При сравнении переменных и неизвестных важно учитывать правила математических операций и применять их для получения точных результатов. Также следует помнить о возможности нахождения решений и интервалов, в которых переменные и неизвестные удовлетворяют сравнениям.

Как сравнивать выражения с помощью математических операций

В математике сравнение выражений осуществляется с помощью различных математических операций. Результаты сравнения могут быть положительными, отрицательными или равными. Давайте рассмотрим основные понятия и примеры сравнения выражений.

Операторы сравнения:

В математике используются следующие операторы сравнения:

• Равно (=): проверяет, равны ли два выражения;
• Не равно (≠): проверяет, не равны ли два выражения;
• Больше (>): проверяет, является ли первое выражение больше второго;
• Меньше (<): проверяет, является ли первое выражение меньше второго;
• Больше или равно (>=): проверяет, является ли первое выражение больше или равным второму;
• Меньше или равно (<=): проверяет, является ли первое выражение меньше или равным второму.

Примеры:

Предположим, у нас есть два выражения: a = 5 и b = 3. Рассмотрим, какие результаты будут получены при сравнении этих выражений с помощью операторов сравнения:

• Выражение a = b вернет false, так как 5 не равно 3;
• Выражение a ≠ b вернет true, так как 5 не равно 3;
• Выражение a > b вернет true, так как 5 больше 3;
• Выражение a < b вернет false, так как 5 не меньше 3;
• Выражение a >= b вернет true, так как 5 больше или равно 3;
• Выражение a <= b вернет false, так как 5 не меньше или равно 3.

Таким образом, сравнение выражений с помощью математических операций позволяет определить, какие выражения больше, меньше или равны друг другу. Это важное понятие в математике, которое находит применение во многих областях науки и техники.

Важность сравнения выражений в математике и его применение в реальной жизни

В математике сравнение выражений применяется во многих областях. Например, в алгебре сравнение выражений используется для решения уравнений и неравенств. Сравнение выражений позволяет нам определить, когда два выражения равны или неравны, и найти их общие решения. Также сравнение выражений используется для построения графиков функций и анализа их свойств.

В финансовой математике сравнение выражений играет важную роль при решении задач, связанных с процентами, инвестициями и кредитами. Например, сравнение процентных ставок позволяет нам определить более выгодную финансовую сделку или выбрать наиболее выгодный кредитный продукт.

В реальной жизни сравнение выражений также является неотъемлемой частью нашей повседневной жизни. Например, при планировании покупок мы сравниваем цены на разные товары, чтобы выбрать наиболее выгодное предложение. При выборе маршрута мы сравниваем время пути и расстояние, чтобы выбрать наиболее оптимальный вариант. В общем, сравнение выражений позволяет нам принимать разумные решения и оптимизировать свою деятельность.

Таким образом, сравнение выражений является важным инструментом в математике и применяется в различных областях нашей жизни. Он позволяет нам получать информацию о свойствах выражений и принимать разумные решения на основе этой информации. Понимание и правильное применение сравнения выражений является необходимым навыком для успешного решения задач и достижения целей в различных сферах нашей жизни.