Что значит в математике отношение одного числа к другому
Содержимое
- 1 Что значит в математике отношение одного числа к другому
- 1.1 Отношение чисел
- 1.2 Раздел 1: Отношение в математике
- 1.3 Раздел 2: Как определить отношение?
- 1.4 Раздел 3: Отношение в виде дроби
- 1.5 Раздел 4: Отношение в процентах
- 1.6 Раздел 5: Отношения в различных областях
- 1.7 Раздел 6: Зависимость между отношениями
- 1.8 Раздел 7: Примеры использования отношений
- 1.9 Раздел 8: Значение отношения в решении математических задач
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое отношение чисел?
- 1.10.0.2 Как вычислить отношение одного числа к другому?
- 1.10.0.3 Можно ли отношение двух чисел представить в виде десятичной дроби?
- 1.10.0.4 Какое значение может иметь отношение чисел?
- 1.10.0.5 Где в математике используется отношение чисел?
- 1.10.0.6 Что такое отношение одного числа к другому в математике?
- 1.10.0.7 Как вычислить отношение одного числа к другому?
- 1.11 Видео по теме:
Отношение одного числа к другому в математике определяется как результат деления одного числа на другое. Это позволяет оценить, сколько раз первое число содержится во втором числе или насколько первое число меньше или больше второго числа. Понимание отношений чисел позволяет решать задачи в областях, таких как пропорции, проценты и скорости.
Отношение — это понятие, основополагающее весьма важную роль в математике. Оно позволяет нам сравнивать и связывать числа друг с другом. Отношение подразумевает существование связи, пропорции или соотношения между двумя числами.
Отношение одного числа к другому показывает, сколько раз одно число содержится в другом. Оно может быть представлено в виде дроби или в процентном выражении. Например, отношение числа 4 к числу 8 можно записать как 4/8 или 50%.
Отношение может быть различного типа, например:
Пропорциональное отношение означает, что два числа связаны постоянным множителем, их отношение всегда остается неизменным. Например, если одно число увеличивается вдвое, то и другое число увеличивается вдвое.
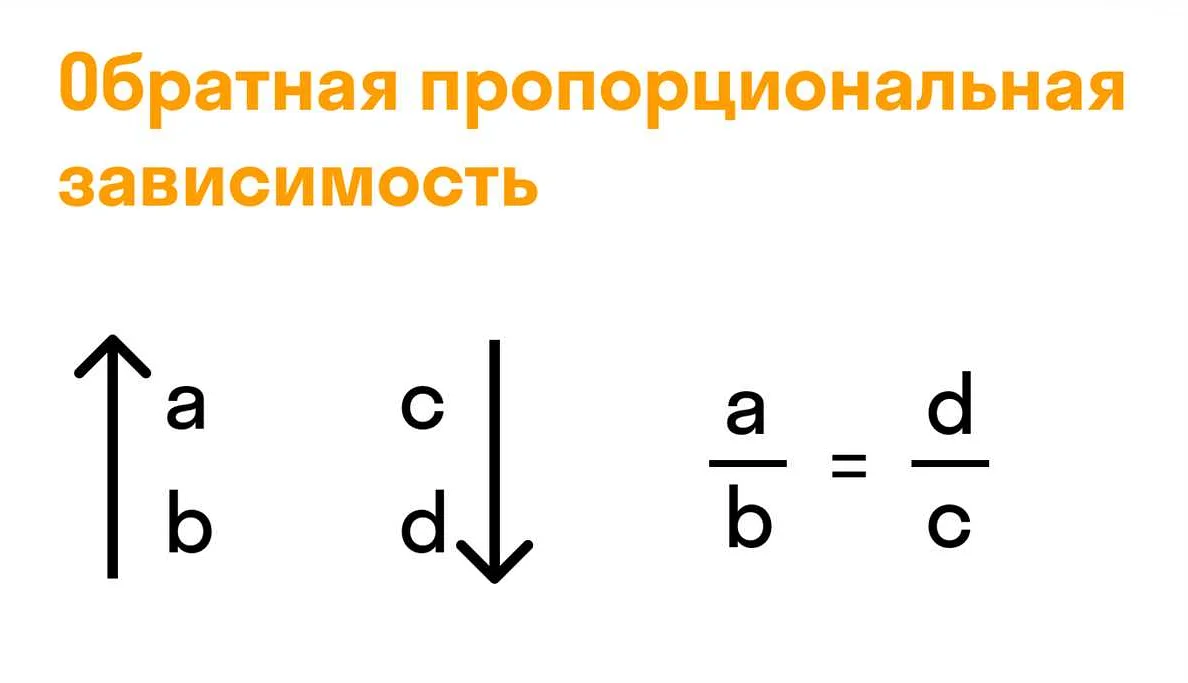
Обратное отношение показывает, что два числа связаны таким образом, что при изменении одного числа другое изменяется в обратном направлении. Например, если одно число увеличится, то другое число уменьшится.
Пропорция — это особый случай отношения, когда четыре числа связаны между собой и их отношение сохраняется.
Отношение одного числа к другому играет важную роль в различных областях математики и науки, а также в повседневной жизни. Понимание и умение работать с отношениями позволяют нам анализировать данные, решать задачи и принимать разумные решения.
Отношение чисел
Отношение одного числа к другому в математике описывает, как одно число связано с другим. Оно показывает, насколько одно число больше или меньше другого.
Отношение чисел можно выразить в виде дроби, где числитель представляет собой первое число, а знаменатель — второе число. Например, если отношение числа 4 к числу 2, то дробь будет выглядеть следующим образом: 4/2.
Отношение чисел также может быть представлено в виде процента или десятичной дроби. Если число 4 связано с числом 2, то отношение будет равно 200% или 2 в десятичной форме.
Отношение чисел часто используется для сравнения двух чисел или для описания изменения одного числа относительно другого. Например, отношение цены товара до и после скидки может показать, насколько снизилась цена.
Отношение чисел также может быть использовано для решения пропорций, где известны отношения нескольких чисел, но одно из них неизвестно. Например, если известно, что отношение чисел A и B равно отношению чисел C и D, то можно найти значение неизвестного числа.
Примеры отношений чиселОписание
| 2/3 | Число 2 связано с числом 3 соотношением 2 к 3 |
| 50% | Число 50 связано с числом 100 соотношением 50% |
| 0.5 | Число 0.5 связано с числом 1 соотношением 0.5 |
В математике отношение чисел является важным инструментом для сравнения и анализа числовых данных. Оно позволяет описать, как одно число связано с другим, и использовать это знание для решения различных задач.
Раздел 1: Отношение в математике
Отношение может быть представлено в виде дроби или как отношение двух чисел, где одно число называется числителем, а другое — знаменателем. Например, в дроби 3/4, число 3 является числителем, а число 4 — знаменателем.
Отношение также может быть представлено в виде процента или десятичной дроби. Например, если имеется отношение 3 к 4, оно может быть представлено как 75% или 0,75 в десятичной форме.
Отношение может быть использовано для сравнения двух чисел или объектов. Например, отношение больше или меньше может быть использовано для сравнения двух чисел и определения, какое из них больше или меньше.
Отношение также может быть использовано для описания зависимостей между объектами. Например, в математической функции отношение может определять, как одно значение зависит от другого.
В математике существует несколько типов отношений, включая равенство, неравенство, пропорциональность и функциональную зависимость. Каждый тип отношения имеет свои особенности и правила, которые могут быть применены для их анализа и решения.
Важно понимать отношение в математике, поскольку оно является основой для решения проблем, моделирования и анализа данных. Понимание отношений поможет вам решать математические задачи и применять их в реальных ситуациях.
Раздел 2: Как определить отношение?
Отношение между двумя числами может быть определено как способ сравнения или сопоставления одного числа с другим. Оно может выражаться в виде доли, процента, отношения чисел или любого другого способа сравнения двух чисел.
Для определения отношения между двумя числами, необходимо сравнить их значительные свойства или характеристики. Например, если мы хотим определить отношение между числами 4 и 8, мы можем сравнить их величины или числовые значения и сказать, что число 8 в два раза больше, чем число 4. Таким образом, отношение между числами 4 и 8 можно выразить как 4:8 или 1:2.
Отношение также может быть определено в виде процента. Например, если мы хотим определить отношение между числами 25 и 50, мы можем сказать, что число 50 составляет 50% от числа 25. Таким образом, отношение между числами 25 и 50 можно выразить как 25:50 или 1:2, или как 50%.
Отношение между числами также может быть выражено в виде отношения чисел друг к другу или как доля. Например, если мы хотим определить отношение между числами 3 и 6, мы можем сказать, что число 6 в два раза больше числа 3. Таким образом, отношение между числами 3 и 6 можно выразить как 3:6 или 1:2, или как доля 1/2.
Определение отношения между числами может быть полезным для сравнения, анализа и понимания их взаимосвязи. Это понятие имеет широкое применение не только в математике, но и в других науках и областях, таких как экономика, физика, социология и т.д.
Раздел 3: Отношение в виде дроби
Например, если мы хотим выразить отношение количества яблок к количеству фруктов в виде дроби, и у нас есть 3 яблока и 10 фруктов, мы можем записать это отношение как 3/10. В данном случае, числитель равен 3, что означает, что у нас есть 3 яблока, а знаменатель равен 10, что означает, что у нас есть 10 фруктов в общем.
Отношение в виде дроби позволяет нам сравнивать и анализировать количество одного объекта в отношении к другому. Это особенно полезно в ситуациях, когда у нас есть данные о количестве объектов или величинах разных типов и мы хотим выразить их отношение. Дробь предоставляет нам инструмент для более точного и удобного описания этого отношения.
ЧислительЗнаменатель
| 3 | 10 |
Раздел 4: Отношение в процентах

В математике, отношение одного числа к другому в процентах используется для выражения соотношения одного значения к другому в виде процентов. Отношение в процентах позволяет лучше понять, насколько одно число больше или меньше другого.
Отношение в процентах выражается в виде десятичной дроби или числа, умноженного на 100 и с символом процента (%). Например, если одно число равно 50, а другое число равно 100, то отношение первого числа ко второму в процентах равно 50%.
Отношение в процентах может быть положительным или отрицательным. Положительное отношение в процентах означает, что первое число больше второго, а отрицательное отношение в процентах — что первое число меньше второго. Например, если одно число равно 60, а другое число равно 80, то отношение первого числа ко второму в процентах равно -25%.
Отношение в процентах широко используется в различных областях, таких как экономика, финансы, статистика и др. Оно помогает сравнивать и анализировать данные, а также делать выводы о том, насколько одно значение отличается от другого.
Для вычисления отношения в процентах необходимо найти разницу между двумя числами, разделить эту разницу на второе число и умножить на 100. Формула для вычисления отношения в процентах выглядит следующим образом:
Формула:
| (Первое число — Второе число) / Второе число * 100 |
Например, для вычисления отношения 60 к 80 в процентах, необходимо выполнить следующие шаги:
ШагДействиеРезультат
| 1 | Вычислить разницу между 60 и 80 | -20 |
| 2 | Разделить -20 на 80 | -0.25 |
| 3 | Умножить -0.25 на 100 | -25% |
Таким образом, отношение числа 60 к числу 80 составляет -25%.
Раздел 5: Отношения в различных областях
В физике отношения применяются для описания взаимосвязей между различными физическими величинами. Например, скорость может быть определена как отношение пройденного пути к затраченному времени. Это позволяет установить зависимость между двумя величинами и изучить их поведение в различных условиях.
В химии отношения используются для определения состава химических соединений. Коэффициенты перед формулами в химических уравнениях показывают отношение между различными реагентами и продуктами реакции. Это позволяет определить пропорции, в которых соединения вступают в реакцию и превращаются в другие вещества.
В экономике отношения используются для анализа финансовых данных и определения показателей эффективности предприятий. Например, отношение прибыли к затратам позволяет оценить рентабельность бизнеса. Отношения также применяются для вычисления индексов, коэффициентов и других показателей, которые позволяют сравнивать и анализировать различные экономические явления.
Отношения также находят применение в различных научных исследованиях, социологии, психологии, информатике и других областях. В каждой из них отношения используются для описания взаимодействий между объектами и определения различных параметров и характеристик.
Таким образом, отношения являются универсальным инструментом для описания и анализа взаимосвязей в различных областях знания.
Раздел 6: Зависимость между отношениями

Когда мы работаем с отношениями между числами, часто возникает вопрос о том, как связаны различные отношения между ними. В математике существуют различные способы определения и изучения зависимости между отношениями.
Одним из основных понятий, используемых для изучения зависимости, является пропорциональность. Пропорциональность между двумя отношениями означает, что они изменяются вместе и в одном и том же соотношении. Например, если отношение A к B пропорционально отношению C к D, то каждое значение отношения A к B соответствует определенному значению отношения C к D.
Есть несколько способов проверить пропорциональность между отношениями. Один из них — использование таблицы соответствия, где значения отношений записываются в две колонки и сравниваются. Если отношения пропорциональны, то значения будут следовать определенному закону пропорции.
Другой способ проверки пропорциональности — использование графика. Если отношения пропорциональны, то точки, представляющие значения отношений, будут лежать на одной прямой линии. Если точки образуют прямую линию, то отношения пропорциональны, если точки разбросаны, то отношения не пропорциональны.
Изучение зависимости между отношениями позволяет нам лучше понять их взаимосвязь и использовать это знание для решения различных задач и проблем. Понимание зависимости между отношениями является важным инструментом в математике и других науках.
Раздел 7: Примеры использования отношений
Пример 1: Проценты
Отношение одного числа к другому часто используется при работе с процентами. Процент обозначает долю или часть чего-либо от целого. Например, если мы говорим о процентах, то мы указываем, какая часть от 100 занимает это число. Например, 50% означает, что мы берем половину от 100, то есть 50.
Пример 2: Доля
Отношение одного числа к другому также может использоваться для работы с долями. Доля обозначает отношение одной части к целому. Например, если мы говорим о долях, то мы указываем, какая часть от целого представляет собой это число. Например, 1/4 означает, что мы берем одну четверть от целого.
Пример 3: Соотношение
Отношение одного числа к другому может также использоваться для определения соотношения между двумя величинами. Например, если мы говорим о соотношении двух величин, то мы указываем, какое число является результатом деления одной величины на другую. Например, если мы говорим о соотношении сторон треугольника, то мы указываем, какое отношение имеют эти стороны друг к другу.
Все эти примеры демонстрируют, как отношение одного числа к другому позволяет нам понять и описать различные аспекты величин и их взаимосвязи. Отношения являются мощным инструментом в математике и находят применение во многих областях, включая экономику, физику, статистику, геометрию и другие.
Раздел 8: Значение отношения в решении математических задач
В решении математических задач отношение может быть использовано для выявления пропорциональности или непропорциональности между двумя величинами. Например, при решении задач на пропорциональное деление или нахождение процента от числа, мы используем отношение одного числа к другому для определения соотношения между этими числами. Это позволяет нам вычислить неизвестные значения или сделать выводы о взаимосвязи между величинами.
Значение отношения также может быть использовано для сравнения двух чисел или наборов чисел. Например, при решении задач на сравнение долей или процентов, мы используем отношение для определения, какая доля или процент больше или меньше. Это помогает нам сравнить и оценить величины и сделать выводы о их относительных размерах.
Кроме того, значение отношения может быть использовано для представления информации о взаимосвязи между числами или величинами. Например, при решении задач на анализ данных или нахождение зависимостей между величинами, мы используем отношение для представления этой взаимосвязи. Это помогает нам понять, как одна величина изменяется в зависимости от другой и сделать выводы о характере этой зависимости.
В заключение, отношение одного числа к другому имеет различное значение в решении математических задач. Оно может быть использовано для сравнения, оценки или представления информации о взаимосвязи между числами или величинами. Понимание значения этого отношения поможет вам успешно решать различные математические задачи и применять полученные знания в реальной жизни.
Вопрос-ответ:
Что такое отношение чисел?
В математике отношение чисел представляет собой сравнение двух чисел, в котором выражается, сколько раз одно число содержится в другом.
Как вычислить отношение одного числа к другому?
Для вычисления отношения чисел необходимо разделить первое число на второе число. Полученное значение является отношением одного числа к другому.
Можно ли отношение двух чисел представить в виде десятичной дроби?
Да, отношение двух чисел можно представить в виде десятичной дроби. Для этого необходимо разделить одно число на другое и записать результат в виде десятичной дроби.
Какое значение может иметь отношение чисел?
Отношение чисел может иметь различные значения в зависимости от чисел, которые сравниваются. Оно может быть равным, больше или меньше единицы, а также равным нулю или неопределенным.
Где в математике используется отношение чисел?
Отношение чисел используется во многих областях математики, таких как алгебра, геометрия, статистика и др. Оно позволяет сравнивать и анализировать числа и их соотношение друг с другом.
Что такое отношение одного числа к другому в математике?
В математике отношение одного числа к другому означает сравнение двух чисел, которое показывает, насколько одно число больше или меньше другого. Отношение обычно выражается в виде дроби или процента.
Как вычислить отношение одного числа к другому?
Для вычисления отношения одного числа к другому, нужно разделить первое число на второе. Например, чтобы найти отношение числа 6 к числу 3, нужно разделить 6 на 3 и получить результат равный 2. Таким образом, отношение числа 6 к числу 3 равно 2.


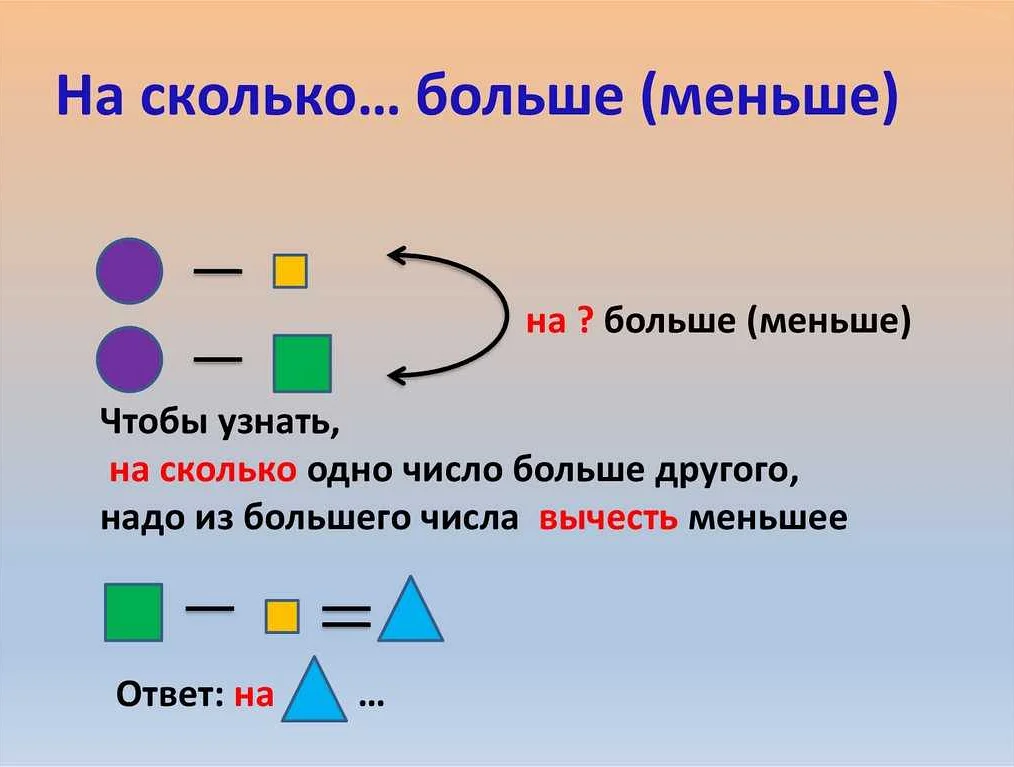


Отношение одного числа к другому в математике — это мера того, насколько одно число больше или меньше другого. Оно позволяет нам сравнивать числа и определять их взаимосвязь. Например, если отношение двух чисел равно 2, это означает, что одно число в два раза больше другого. Отношение можно представить в виде дроби, где числитель — это первое число, а знаменатель — второе число. Числитель показывает, на сколько первое число больше или меньше второго. Знаменатель показывает, какое количество частей составляет второе число от первого. Например, отношение 2:1 означает, что первое число в два раза больше второго или второе число составляет половину от первого. Отношение чисел играет важную роль во многих областях жизни, таких как финансы, наука, технологии и другие. Понимание отношения чисел помогает нам анализировать данные, делать выводы и принимать решения на основе математических расчетов.
Отношение одного числа к другому в математике является важным понятием, которое помогает нам понять и сравнить числа. Когда мы говорим о отношении чисел, мы обычно имеем в виду их сравнение в том, какое число больше или меньше другого. Отношение одного числа к другому можно выразить с помощью математической операции деления. Если одно число делится на другое без остатка, то отношение будет равно целому числу. Например, отношение числа 10 к числу 5 равно 2, потому что 10 делится на 5 без остатка. Когда отношение чисел не является целым числом, мы можем выразить его в виде десятичной дроби или процента. Например, отношение числа 3 к числу 4 можно записать как десятичную дробь 0.75 или как процент 75%. Отношение чисел также может быть выражено с помощью соотношений или пропорций. Например, если отношение числа A к числу B равно 2, а отношение числа C к числу D равно 3, мы можем сказать, что отношение числа A к числу B пропорционально отношению числа C к числу D. В математике отношение чисел играет важную роль во многих областях, таких как алгебра, геометрия и статистика. Оно помогает нам сравнивать и анализировать числа, а также решать различные задачи и проблемы.
Отношение одного числа к другому в математике является ключевым понятием, которое помогает нам понять, как два числа связаны между собой. Это позволяет нам сравнивать и анализировать числа, чтобы получить более полное представление о их значении. Отношение двух чисел выражается в виде дроби, где числитель представляет одно число, а знаменатель — другое. Значение этой дроби определяет соотношение между двумя числами. Например, если отношение равно 1/2, это означает, что одно число в два раза меньше другого. Отношение чисел может быть выражено в виде процента или десятичной дроби. Процентное отношение показывает, сколько процентов составляет одно число от другого. Десятичная дробь представляет отношение в десятичном виде. Отношение одного числа к другому имеет большое значение в различных областях математики, физики, экономики и других наук. Оно позволяет нам сравнивать данные, делать прогнозы и принимать решения на основе числовых факторов. В заключение, понимание отношения одного числа к другому помогает нам анализировать и интерпретировать числовую информацию. Это важный инструмент для решения различных задач и принятия обоснованных решений.
Отношение одного числа к другому — это понятие из математики, которое позволяет сравнивать и анализировать числа. В основе отношения лежит понятие доли или долей. Например, если у нас есть два числа: 10 и 5, то отношение числа 10 к числу 5 будет равно 2. Это означает, что первое число в два раза больше второго числа. Отношение чисел можно выразить в виде десятичной дроби, процента или просто в виде обыкновенной дроби. Отношение чисел играет важную роль в решении задач и анализе данных. Например, при сравнении цен на товары или при расчете процентов. Понимание отношения чисел помогает нам лучше понять мир вокруг нас и применять математику на практике.