Увеличить что это значит в математике

Увеличить в математике означает увеличение значения числа на определенную величину или процент. Узнайте, как выполнять увеличение чисел и применять его в различных математических операциях.

Увеличение — это понятие, которое широко используется в математике для описания процесса увеличения или увеличенного значения чего-либо. В математике, увеличение обычно означает увеличение числа, размера, значения или других количественных характеристик. Это действие может быть выполнено путем добавления или умножения числа на определенную величину или процент.

Важно отметить, что увеличение может быть как положительным, так и отрицательным. Положительное увеличение означает увеличение значения, тогда как отрицательное увеличение означает уменьшение значения. Например, если увеличение числа на 10%, значение увеличится на 10%. Однако, если увеличение числа на -10%, значение уменьшится на 10%.

Пример:

Допустим, у вас есть число 20 и вы хотите его увеличить на 30%. Чтобы это сделать, вам нужно найти 30% от числа 20 и добавить это значение к 20. 30% от 20 равно 6, поэтому, чтобы увеличить число 20 на 30%, нужно прибавить 6 к 20. Получается, 20 + 6 = 26. Таким образом, увеличение числа 20 на 30% дает 26.

Увеличение имеет широкое применение в различных областях математики, физики, экономики и других наук. Оно позволяет анализировать и описывать изменения величин и их взаимосвязи. Понимание понятия увеличения и умение применять его в решении задач является важной компетенцией в математике и других дисциплинах, где количественные характеристики имеют значение.

Что означает «увеличить» в математике?

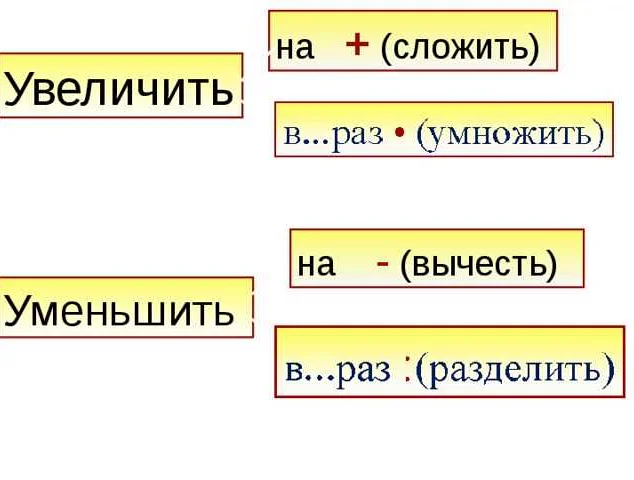
В математике термин «увеличить» используется для обозначения операции, которая увеличивает значение числа или величины. Увеличение может происходить на определенную величину или в процентном соотношении.

В случае увеличения на определенную величину, к исходному числу или величине прибавляется заданное число. Например, если имеется число 5 и нужно его увеличить на 3, то результатом операции будет число 8.

В случае увеличения в процентном соотношении, к исходному числу или величине прибавляется определенный процент. Например, если имеется число 50 и нужно его увеличить на 20%, то результатом операции будет число 60.

Увеличение в математике может быть применено к различным объектам, например к числам, длинам, площадям, объемам и т. д. Важно понимать контекст и заданные условия задачи, чтобы правильно применить операцию увеличения и получить нужный результат.

Примеры увеличения в математике:

Увеличение числа 7 на 2: 7 + 2 = 9

Увеличение длины отрезка на 10%: 100 см + 10% = 110 см

Увеличение площади квадрата на 50%: 10 кв. см + 50% = 15 кв. см

Определение термина «увеличить»

В математике, термин «увеличить» относится к операции, которая приводит к увеличению значения числа или величины. Увеличение может происходить путем прибавления определенного значения или изменения масштаба.

Например, если у нас есть число 5 и мы хотим его увеличить на 3, мы просто прибавляем 3 к 5 и получаем результат 8. Также можно увеличить число, умножив его на определенный коэффициент. Например, если мы умножим число 5 на 2, мы получим 10, что является увеличением исходного значения в два раза.

Увеличение может быть применено не только к числам, но и к другим величинам, таким как площадь, объем, скорость и другие. Например, площадь квадрата можно увеличить, увеличивая длину его стороны, а скорость можно увеличить, увеличивая количество пройденного пути за единицу времени.

Важно отметить, что увеличение является относительным понятием и зависит от исходного значения. Например, увеличение числа 5 на 3 будет давать результат 8, но увеличение числа 10 на 3 даст результат 13.

Примеры увеличения чиселПримеры увеличения величин

5 + 3 = 8	Увеличение площади квадрата путем увеличения стороны
10 + 3 = 13	Увеличение скорости путем увеличения пройденного пути
7 * 2 = 14	Увеличение объема путем увеличения всех его измерений

Важность понимания понятия «увеличить»

В математике, «увеличить» означает увеличение числовой величины, объекта или значения на определенную величину или процент. Это может быть как увеличение числа само по себе, так и увеличение его значения в рамках определенной системы или сравнения с другими числами.

Понимание понятия «увеличить» особенно важно при работе с пропорциями, процентами и изменениями величин. Знание того, как правильно увеличивать числа или объекты, позволяет нам решать задачи по пропорциональности, находить процентные отношения и анализировать изменения величин в различных ситуациях.

Примером важности понимания понятия «увеличить» может служить задача о расчете скидки на товар. Если мы не понимаем, как правильно увеличивать цену товара для расчета скидки, мы можем сделать ошибку и получить неверный результат. Но если мы точно знаем, что «увеличить» означает добавить определенную сумму или процент к стоимости товара, мы сможем правильно рассчитать скидку и получить корректный ответ.

Таким образом, понимание понятия «увеличить» в математике является важным навыком, который помогает нам более точно и эффективно работать с числами и объектами в различных ситуациях. Это понимание позволяет нам правильно решать задачи, анализировать изменения и применять различные математические концепции для получения правильных результатов.

Примеры увеличения чисел и величин

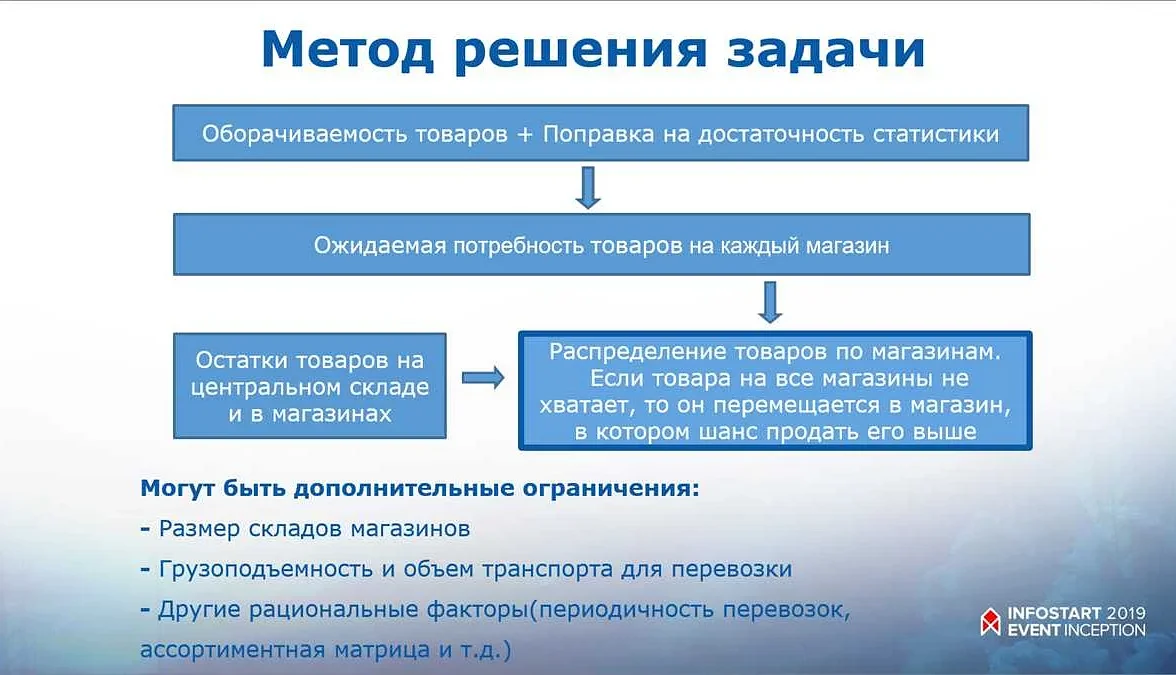
Увеличение числа или величины в математике означает увеличение их значения или размера. Рассмотрим несколько примеров увеличения чисел и величин:

1. Увеличение числа на 5. Например, если у нас есть число 10, то его увеличение на 5 даст нам число 15.
2. Увеличение процента. Если у нас есть число 100, и мы хотим увеличить его на 20%, то сначала находим 20% от 100 (20) и добавляем это значение к исходному числу. В итоге получаем число 120.
3. Увеличение длины отрезка. Например, у нас есть отрезок длиной 5 единиц, и мы хотим увеличить его на 3 единицы. В результате получим отрезок длиной 8 единиц.
4. Увеличение площади прямоугольника. Если у нас есть прямоугольник с площадью 10 квадратных единиц, и мы хотим увеличить его площадь на 4 квадратных единицы, то итоговая площадь будет равна 14 квадратным единицам.

Таким образом, увеличение чисел и величин в математике означает увеличение их значений или размеров в соответствии с заданными правилами и операциями.

Увеличение чисел на конкретную величину

В математике понятие «увеличить» означает прибавление к числу определенной величины. Это позволяет получить новое число, которое больше исходного.

Для увеличения чисел на конкретную величину используется операция сложения. Например, если у нас есть число 5 и мы хотим его увеличить на 3, то мы просто прибавляем 3 к 5 и получаем новое число — 8.

Давайте рассмотрим примеры увеличения чисел на конкретную величину:

Исходное числоУвеличение наНовое число

2	4	6
10	7	17
8	2	10

Таким образом, увеличение чисел на конкретную величину позволяет получить новое число, которое больше исходного на указанную величину. Это осуществляется путем операции сложения.

Процентное увеличение чисел

Для вычисления процентного увеличения числа необходимо выполнить следующие шаги:

1. Найти разницу между новым и старым значением числа.
2. Разделить эту разницу на исходное значение числа.
3. Умножить полученное значение на 100, чтобы получить процентное значение.

Давайте рассмотрим пример. Представим, что у нас есть число 50, которое увеличилось до 75. Чтобы вычислить процентное увеличение, мы должны выполнить следующие вычисления:

Исходное значениеНовое значениеРазницаПроцентное увеличение

50

75

75 — 50 = 25

(25 / 50) * 100 = 50%

Таким образом, процентное увеличение числа 50 до 75 составляет 50%.

Процентное увеличение чисел является важным математическим концептом, используемым во многих сферах, таких как экономика, финансы, статистика и т.д. Умение вычислять процентное увеличение позволяет анализировать и сравнивать изменения величин и делать выводы на основе полученных данных.

Значение увеличения в графиках и диаграммах

Увеличение играет важную роль при анализе и интерпретации графиков и диаграмм. Оно позволяет получить детальную информацию о данных и выделить особенности представленных значений.

При увеличении графика мы увеличиваем масштаб, тем самым увеличивая все значения по осям координат. Это позволяет нам более подробно рассмотреть зависимости и тренды в данных. Например, если у нас есть график, отображающий изменение температуры в течение дня, увеличение может помочь нам увидеть более мелкие колебания и понять, как меняется температура в разные периоды времени.

В диаграммах увеличение также может быть полезным инструментом для анализа данных. Например, если у нас есть круговая диаграмма, показывающая распределение продаж по различным товарным категориям, увеличение может помочь нам выделить категории с наибольшими и наименьшими продажами. Таким образом, мы сможем лучше понять структуру продаж и определить приоритетные направления развития бизнеса.

Увеличение в графиках и диаграммах позволяет нам углубиться в данные и получить более точное представление о представленной информации. Это важнейший инструмент для аналитиков и исследователей, позволяющий делать более точные выводы и принимать обоснованные решения на основе предоставленных данных.

Вопрос-ответ:

Что означает понятие «увеличить» в математике?

В математике понятие «увеличить» означает увеличение числа или величины на определенное количество или процент. Это может быть увеличение числа на определенную величину или умножение числа на коэффициент. Например, если число равно 5, и его увеличить на 3, то получится число 8.

Какие могут быть примеры увеличения чисел в математике?

Примеры увеличения чисел в математике могут быть разными. Например, если увеличить число 10 на 5, то получится число 15. Если увеличить число 7 на 20%, то получится число 8,4. Увеличение чисел может осуществляться как сложением, так и умножением на коэффициент.

Какие методы увеличения чисел существуют в математике?

В математике существуют разные методы увеличения чисел. Один из них — сложение числа с другим числом. Например, если увеличить число 3 на 2, то нужно прибавить к нему число 2 и получится 5. Другой метод — умножение числа на коэффициент. Например, если увеличить число 4 на 50%, то нужно умножить его на 1,5 и получится 6.

Как увеличивать дробные числа в математике?

Дробные числа в математике также можно увеличивать. Для этого можно умножить дробное число на коэффициент. Например, если увеличить число 0,5 на 20%, то нужно умножить его на 1,2 и получится 0,6. Также можно увеличивать дробные числа путем сложения их с другими числами. Например, если увеличить число 0,3 на 0,2, то получится число 0,5.

Можно ли увеличить число на бесконечность в математике?

В математике нельзя увеличить число на бесконечность. Бесконечность не является числом и не имеет конкретного значения. Поэтому операции увеличения или уменьшения на бесконечность не имеют смысла. Бесконечность можно только рассматривать как понятие или предел.

Какое определение имеет слово «увеличить» в математике?

В математике слово «увеличить» означает увеличение числа или значения величины на определенную величину или процент.

Можете привести примеры использования понятия «увеличить» в математике?

Конечно! Например, если у вас есть число 5, а вы его увеличиваете на 3, то получите число 8. Также, если у вас есть длина стороны квадрата, равная 4, а вы увеличиваете ее вдвое, то получите сторону длиной 8. В математике понятие «увеличить» используется для изменения числовых значений и размеров объектов.

Практическое применение увеличения в математике

Одним из практических применений увеличения является геометрия. Например, при построении карт и планов увеличение используется для изменения масштаба объектов, чтобы они могли быть отображены на более удобном и понятном уровне. Увеличение также применяется в планировании городской инфраструктуры, архитектуре и дизайне для изменения размеров зданий и других объектов.

В физике увеличение используется при измерении и анализе объектов. Например, микроскоп использует увеличение для увеличения изображения маленьких объектов, чтобы исследователи могли увидеть и изучить их более детально. Телескопы также используют увеличение для увеличения видимости далеких объектов в космосе.

В экономике и бизнесе увеличение используется для оценки и анализа данных. Например, увеличение может быть применено к доле рынка, объему продаж или прибыли для определения изменения величины во времени. Увеличение также может использоваться для прогнозирования будущих значений и разработки стратегий для достижения желаемых результатов.

В компьютерной графике увеличение используется для изменения размера изображений. Например, при масштабировании фотографии или рисунка увеличение позволяет увеличить детали и улучшить качество изображения.

В образовании увеличение используется для улучшения понимания математических концепций. Например, увеличение может быть использовано для визуализации умножения или деления чисел, чтобы студенты могли более ясно представить себе процесс и получить правильный ответ.

В заключение, увеличение — это важная операция в математике, которая имеет широкое практическое применение в различных областях. Она позволяет изменять размер и масштаб объектов, а также анализировать данные и улучшать понимание различных концепций. Понимание и использование увеличения в математике помогает нам решать разнообразные задачи и применять ее в реальной жизни.

Видео по теме: