Увеличение в математике это что

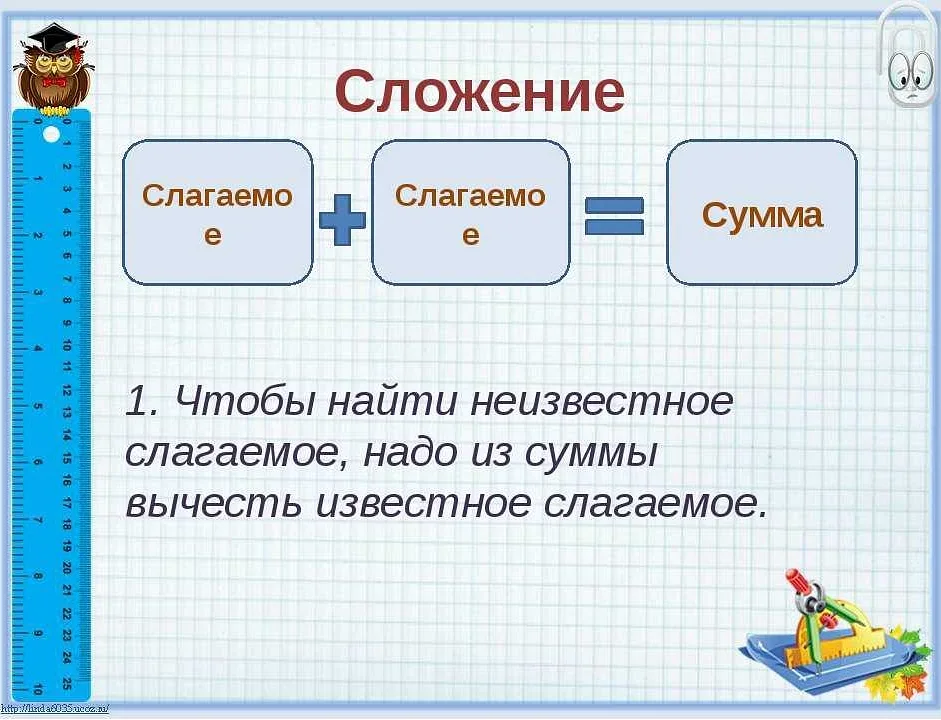
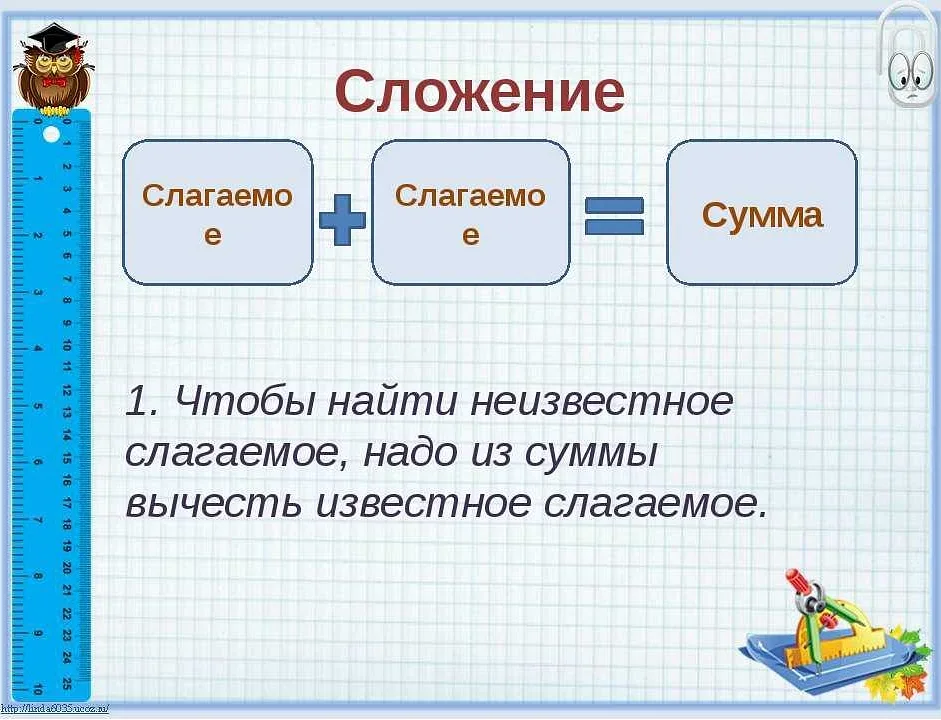
Увеличение в математике – это процесс увеличения значения числа, количества, площади или объема с помощью определенных операций и правил. Увеличение может быть применено в различных математических задачах и рассматривается как основной элемент арифметики. Умение правильно увеличивать числа и вычислять увеличение позволяет решать разнообразные задачи и использовать математику в повседневной жизни.

Увеличение — это одна из ключевых операций в математике, которая позволяет увеличивать значение числа или величины. Оно широко применяется в различных областях, начиная от простых расчетов и заканчивая сложными научными исследованиями.

Основная цель увеличения — получить новое значение числа или величины, которое больше предыдущего. Это может быть полезно, например, при решении задач по финансам, анализе данных, строительстве и других областях, где требуется увеличение значения.

Применение увеличения в математике может быть очень разнообразным. Например, в финансовой сфере увеличение используется для рассчета процентов по депозитам, кредитам и другим финансовым операциям. В научных исследованиях увеличение может быть полезно, чтобы увеличить точность измерений или изменить масштаб исследуемого объекта.

Применение увеличения в математике позволяет получить более точные результаты и расширить область применимости математических моделей. Оно открывает новые возможности для решения различных задач и обеспечивает точность и надежность в расчетах и исследованиях.

В заключение, увеличение в математике является важной операцией, которая находит применение в различных областях. Оно позволяет увеличивать значения чисел и величин, что является неотъемлемой частью математических расчетов и исследований. Знание и применение увеличения помогает получить более точные результаты и расширить границы возможностей математики.

Определение увеличения

В контексте математических задач, увеличение может быть выражено числами или процентами. Например, если начальное значение равно 10, а увеличение составляет 20%, то конечное значение будет равно 12.

Увеличение может быть положительным или отрицательным, в зависимости от того, увеличивается ли значение или уменьшается. Например, увеличение на 10 может быть положительным, а увеличение на -5 будет отрицательным.

Увеличение широко применяется в различных областях математики, таких как финансы, экономика, статистика и геометрия. Оно может быть использовано для решения задач, связанных с процентами, ростом, изменением размеров и масштабов, а также для анализа данных и построения моделей.

Важно понимать, что увеличение в математике не является простым увеличением в повседневной жизни. Оно имеет строгие математические определения и правила, которые необходимо учитывать при его использовании.

Знание определения увеличения в математике позволяет более точно и эффективно работать с числами и данными, а также решать различные задачи, связанные с изменением величин.

Основные понятия и термины

При изучении увеличения в математике важно понимать основные понятия и термины, которые связаны с этой темой.

Увеличение — это процесс увеличения размеров или количества чего-либо. В математике увеличение часто относится к увеличению чисел или величин.

Масштаб — это отношение между длиной отрезка на рисунке и соответствующей длиной в реальном мире. Масштаб позволяет увеличивать или уменьшать объекты на рисунке с сохранением пропорций.

Пропорция — это равенство двух отношений. В контексте увеличения в математике, пропорция используется для определения соотношения между увеличенными и исходными значениями.

Масштабный множитель — это число или коэффициент, которое используется для увеличения или уменьшения числа или величины. Масштабный множитель применяется к исходному значению, чтобы получить увеличенное или уменьшенное значение.

Увеличение в процентах — это увеличение числа или величины на определенный процент. Увеличение в процентах может быть положительным (увеличение) или отрицательным (уменьшение).

Увеличение с постоянным множителем — это увеличение числа или величины на постоянное значение. При увеличении с постоянным множителем исходное значение умножается на постоянное число, чтобы получить увеличенное значение.

Примеры использования увеличения

ПримерОписание

1	Финансы: Расчеты процентов по вкладам или кредитам
2	Наука: Изучение пропорциональных связей в физике или химии
3	Инженерия: Расчеты масштабов в строительстве или проектировании
4	Техника: Увеличение изображений в фотографии или видеозаписи

Примеры использования увеличения показывают, как этот математический метод применяется для решения разнообразных задач и упрощения сложных вычислений. Увеличение позволяет находить неизвестные значения, используя пропорциональные соотношения, что делает его очень полезным инструментом в различных областях науки и техники.

Практические примеры

Давайте рассмотрим несколько практических примеров увеличения:

ПримерИсходное числоПроцент увеличенияРезультат

Пример 1	100	10%	110
Пример 2	2000	5%	2100
Пример 3	50	20%	60

Как видим, в каждом примере исходное число увеличивается на определенный процент. Для расчета результата мы можем использовать формулу:

Результат = Исходное число + (Исходное число * Процент увеличения)

Надеюсь, эти примеры помогут вам понять, как применять увеличение в математике на практике. Он может быть полезен при решении различных задач и расчетов.

Увеличение в геометрии

Увеличение выполняется путем умножения координат всех точек объекта на одно и то же число, называемое коэффициентом увеличения. Если коэффициент увеличения больше 1, то объект становится больше, а если он меньше 1, то объект уменьшается. Коэффициент увеличения может быть как положительным, так и отрицательным. Если коэффициент увеличения равен 1, то объект остается без изменений.

Увеличение может быть однородным, когда все точки объекта увеличиваются на одно и то же число, и неоднородным, когда каждая точка объекта увеличивается на разные числа.

Увеличение в геометрии широко применяется в различных областях, таких как архитектура, дизайн, инженерия и т.д. Оно позволяет изменять размеры и пропорции объектов, что является важным при создании моделей, чертежей и проектов.

При работе с увеличением в геометрии необходимо учитывать основные принципы и правила, такие как сохранение пропорций, сохранение параллельности и перпендикулярности. Также важно уметь работать с масштабными моделями и изображениями, чтобы представить объекты в нужном масштабе и размере.

В заключение, увеличение в геометрии является важной операцией, которая позволяет изменять размеры объектов без изменения их формы и пропорций. Оно находит широкое применение в различных областях и требует понимания основных принципов и правил работы с ним.

Применение увеличения в пространстве

Одним из основных применений увеличения в пространстве является изменение масштаба 3D-моделей. Увеличение позволяет изменить размер объекта в трехмерном пространстве, сохраняя его пропорции. Это особенно полезно при создании архитектурных моделей, где необходимо увеличить или уменьшить размер здания или деталей.

Увеличение также широко используется в геометрии при решении задач, связанных с построением и измерением фигур. Например, при увеличении треугольника или прямоугольника можно изменить его размеры, сохраняя при этом пропорциональные отношения между сторонами и углами. Это позволяет упростить вычисления и решение задач, связанных с геометрией.

Еще одним применением увеличения в пространстве является использование его в физике. Увеличение может быть использовано для изучения масштабов объектов в микро- и макромасштабе. Например, при исследовании атомных частиц или галактик увеличение позволяет увидеть детали и структуру объектов, которые не могут быть видны невооруженным глазом.

Таким образом, применение увеличения в пространстве имеет широкий спектр применений и полезно во многих областях. Оно позволяет изменять размеры объектов, сохраняя их пропорции, и облегчает решение задач, связанных с геометрией и физикой. Эта операция играет важную роль в понимании и изучении мира вокруг нас.

Увеличение в алгебре

Увеличение числа на определенную величину можно выполнить, сложив данное число с этой величиной. Например, чтобы увеличить число 5 на 3, нужно прибавить к нему 3:

• 5 + 3 = 8

Увеличение числа на процент производится с помощью формулы:

• новое значение = исходное значение + (исходное значение * процентный коэффициент)

Например, если нужно увеличить число 10 на 20%, то расчет будет следующим образом:

• новое значение = 10 + (10 * 0.2) = 10 + 2 = 12

Увеличение переменной в алгебре осуществляется аналогично увеличению числа. Например, если есть переменная «x», и нужно увеличить ее на 2, то результат будет следующим:

• x + 2

Таким образом, увеличение в алгебре является важной операцией, которая позволяет изменить значение числа или переменной и использовать его в дальнейших вычислениях.

Понятие увеличения в алгебре

Увеличение в алгебре может быть использовано для решения различных задач. Например, если у нас есть начальное значение и мы знаем, на сколько его нужно увеличить каждый раз, мы можем использовать увеличение для определения значения на определенном шаге.

Также, увеличение может быть использовано в алгебре для выражения изменения значения величины. Например, если у нас есть начальное значение и мы хотим выразить его изменение на определенную величину, мы можем использовать увеличение для записи этого изменения.

В алгебре увеличение может быть использовано вместе с другими операциями, такими как вычитание и умножение, для выполнения сложных вычислений. Например, мы можем использовать увеличение и вычитание для определения разницы между двумя значениями.

В заключение, понятие увеличения в алгебре является важным инструментом, который позволяет нам выполнять различные операции с числами и выражать изменение значений. Понимание этого понятия поможет нам улучшить наши навыки в математике и решать сложные задачи более эффективно.

Видео по теме:

Вопрос-ответ:

Что такое увеличение в математике?

Увеличение в математике — это операция, позволяющая увеличить значение числа или величины на определенную величину или процент. Оно применяется, когда необходимо увеличить какую-либо величину на определенное количество или проценты.

Как применять увеличение в математике?

Увеличение в математике применяется путем добавления определенного значения или процента к исходному числу или величине. Для увеличения числа на определенное значение, необходимо к исходному числу прибавить это значение. Для увеличения числа на определенный процент, необходимо умножить исходное число на этот процент и сложить результат с исходным числом. Пример: для увеличения числа 10 на 20%, нужно умножить 10 на 0.2 (20% в десятичной форме) и сложить результат с 10, получив 12.

Зачем нужно увеличение в математике?

Увеличение в математике используется для решения различных задач и ситуаций. Например, его можно применять для расчета увеличения цены товара после наложения на нее налога, для определения увеличения населения в городе после определенного периода времени, а также для установления процента увеличения прибыли в бизнесе. В общем, увеличение в математике позволяет анализировать и прогнозировать изменения величин и их влияние на различные процессы.

Какие еще есть способы увеличения чисел в математике?

Помимо простого увеличения на определенное значение или процент, существуют и другие способы увеличения чисел в математике. Например, можно использовать множители для увеличения числа на определенное количество раз. Также можно применять геометрические прогрессии или арифметические операции для увеличения числа. Важно выбрать подходящий метод в зависимости от конкретной задачи и условий.

Какую ошибку можно допустить при применении увеличения в математике?

Одной из ошибок, которую можно допустить при применении увеличения в математике, является неправильное определение значения или процента, на которые нужно увеличить исходное число или величину. Неправильный выбор значения или процента может привести к неверному результату. Поэтому важно внимательно анализировать условия задачи и правильно определять, насколько нужно увеличивать исходное число или величину.

Что такое увеличение в математике?

Увеличение в математике — это операция, которая увеличивает число или величину на определенное количество единиц или процентов. Оно используется для изменения числовых значений в задачах, расчетах или анализе данных.

Как применять увеличение в математике?

Увеличение в математике может быть использовано в различных сферах и задачах. Например, в экономике для расчета процентного изменения цен, в геометрии для изменения размеров фигур, или в статистике для анализа роста показателей. Применение увеличения зависит от конкретной ситуации и требований задачи.

Практическое применение увеличения

Одним из самых распространенных примеров практического применения увеличения является графический дизайн. Дизайнеры часто используют масштабирование, чтобы изменить размеры изображений, логотипов, иконок и других элементов дизайна. Это позволяет им адаптировать контент под различные устройства, такие как мобильные телефоны, планшеты или настольные компьютеры.

В компьютерной графике также широко применяется увеличение. Например, в 3D-моделировании увеличение позволяет создавать детализированные объекты, учитывая каждую маленькую деталь. Это особенно полезно при создании игр, анимации, мультфильмов и визуализации архитектурных проектов.

Увеличение также играет важную роль в фотографии. Фотографы используют масштабирование, чтобы увеличить мелкие детали на изображении, улучшить резкость и качество фото. Это позволяет им создавать высококачественные снимки и работать с фотографиями различных форматов и разрешений.

Кроме того, увеличение находит применение в науке и технике. В области медицины, например, увеличение позволяет врачам исследовать мелкие структуры организма и выявлять патологии. В инженерии увеличение помогает разрабатывать точные и детализированные чертежи, а также анализировать и моделировать сложные системы.

Таким образом, практическое применение увеличения весьма разнообразно и значимо. Оно позволяет нам работать с различными видами данных, изображений и объектов, обеспечивая высокую точность, качество и удобство использования.

Примеры применения в реальной жизни

1. В экономике: увеличение используется для расчета процентных ставок, инфляции, экономического роста и других финансовых показателей.
2. В географии: увеличение позволяет создавать и анализировать карты, глобусы и другие географические модели.
3. В физике: увеличение используется для расчета масштабов и пропорций в различных физических явлениях, таких как движение, сила и энергия.
4. В архитектуре: увеличение позволяет создавать и анализировать планы зданий, чертежи и другие архитектурные проекты.
5. В медицине: увеличение используется для изучения и анализа медицинских изображений, таких как рентгеновские снимки и МРТ.
6. В технике: увеличение применяется для разработки и тестирования различных механизмов и устройств.

Это лишь несколько примеров того, как увеличение в математике применяется в реальной жизни. Понимание этого понятия помогает нам решать различные задачи и применять математические знания для решения практических проблем.