Что значит выражение имеет смысл в математике

Выражение имеет смысл в математике, если оно является логически верным и может быть вычислено или рассмотрено с помощью математических операций и правил. Умение определить смысл выражения в математике позволяет нам анализировать и решать разнообразные задачи и проблемы с использованием точных математических методов и средств.

В математике понятие о смысле выражения является одним из основных. Оно помогает определить, действительно ли данное выражение имеет математическое значение и может быть вычислено. Если выражение имеет смысл, то оно соответствует определенным правилам и может быть оценено с помощью математических операций.

Чтобы понять, что выражение имеет смысл, нужно учесть несколько факторов. Во-первых, нужно обратить внимание на наличие всех необходимых переменных и констант в выражении. Если выражение содержит неизвестные значения, оно может иметь смысл только при условии, что значения этих переменных определены. Во-вторых, нужно убедиться, что выражение не включает недопустимых операций, таких как деление на ноль или извлечение квадратного корня из отрицательного числа.

Пример выражения, имеющего смысл, это алгебраическое выражение вида 2x + 5, где x — переменная. Данное выражение имеет смысл, так как содержит только одну переменную и может быть вычислено при заданном значении для x. Например, при x = 3, выражение примет значение 2*3 + 5 = 11.

Важно понимать, что выражение может иметь смысл в одном контексте и не иметь его в другом. Например, выражение 1/0 не имеет смысла в обычной арифметике, так как деление на ноль не определено. Однако, в математическом анализе такие выражения могут иметь смысл и рассматриваться как пределы функций или бесконечности.

Определение понятия «имеет смысл» в математике

Аргументы выражения «имеют смысл», если они являются допустимыми входными данными для данной математической операции или функции. Например, в выражении «x + y», аргументы «x» и «y» могут быть любыми числовыми значениями, такими как целые числа или десятичные дроби. Однако, если аргументы не могут быть определены или не соответствуют требованиям операции или функции, то выражение «не имеет смысла».

Операции и функции выражения «имеют смысл», когда они имеют определение и корректно работают с заданными аргументами. Например, в выражении «x + y», операция сложения имеет смысл, так как она определена для числовых значений и выполняет сложение. Однако, если выражение содержит операцию или функцию, которая не определена или не может быть выполнена с заданными аргументами, то выражение «не имеет смысла».

Примеры выражений, которые «имеют смысл» в математике:

• «2 + 3» — выражение имеет смысл, так как операция сложения определена для числовых значений 2 и 3.
• «5 / 2» — выражение имеет смысл, так как операция деления определена для числовых значений 5 и 2, и возвращает результат в виде десятичной дроби.
• «sqrt(9)» — выражение имеет смысл, так как функция квадратного корня определена для числового значения 9, и возвращает результат в виде числа 3.

Примеры выражений, которые «не имеют смысла» в математике:

• «2 + apple» — выражение не имеет смысла, так как операция сложения не определена для числового значения 2 и нечислового значения «apple».
• «1 / 0» — выражение не имеет смысла, так как операция деления не определена для числового значения 1 и нуля, и вызывает деление на ноль, что является некорректным.
• «log(-10)» — выражение не имеет смысла, так как функция логарифма не определена для отрицательных числовых значений, и вызывает ошибку.

Почему важно, чтобы выражение имело смысл в математике

В математике, понимание и использование корректных выражений крайне важно. Когда выражение имеет смысл, оно может быть анализировано и использовано для получения конкретных результатов и выводов. Вот несколько причин, почему важно, чтобы выражение имело смысл в математике:

1. Понимание и коммуникация: Математика является универсальным языком, который используется для выражения и обмена идеями и концепциями. Когда выражение имеет смысл, оно позволяет математикам точно и ясно коммуницировать между собой.
2. Точность и надежность: Выражения, которые имеют смысл, обеспечивают точные и надежные результаты при проведении математических операций. Если выражение не имеет смысла, то результаты могут быть неправильными или непредсказуемыми.
3. Решение проблем: Математика используется для решения различных проблем и задач. Когда выражение имеет смысл, оно помогает нам разобраться в проблеме и применить нужные математические методы для ее решения.
4. Математические модели: Математические модели используются для описания и изучения реальных явлений и процессов. Когда выражение имеет смысл, оно позволяет нам создавать и анализировать математические модели, которые помогают в понимании и предсказании сложных систем.
5. Разработка новых теорий и открытий: Математика постоянно развивается и расширяется. Когда выражение имеет смысл, оно может быть использовано для разработки новых теорий, формулирования гипотез и делания открытий в математике.

В итоге, понимание и использование выражений, которые имеют смысл в математике, является необходимым условием для достижения точности, надежности и успеха в этой науке.

Примеры выражений, которые имеют смысл в математике

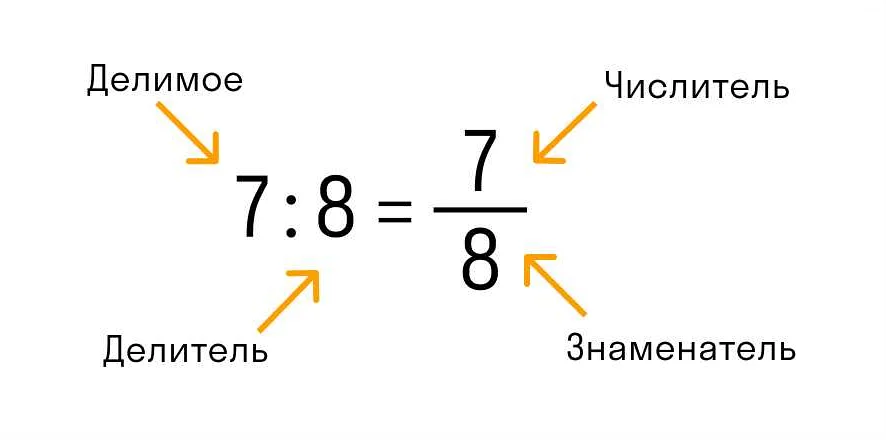
В математике много выражений, которые имеют смысл и используются для решения различных задач. Некоторые из них включают:

Пример выраженияОписание

2 + 3	Сложение двух чисел
5 — 2	Вычитание одного числа из другого
4 * 6	Умножение двух чисел
8 / 2	Деление одного числа на другое
x + 5	Сложение переменной с числом
3x — 2y	Вычитание переменных
2a * b	Умножение переменных
10 / x	Деление числа на переменную
(x + 3)(x — 2)	Умножение двух скобок

Это только некоторые из множества выражений, которые могут быть использованы в математике для решения задач различного уровня сложности. Выражения позволяют нам работать с числами и переменными, выполнять арифметические операции и получать новые значения.

Как определить, имеет ли выражение смысл в математике

В математике, для того чтобы выражение имело смысл, оно должно быть корректно сформулировано и иметь определенное значение или свойство. Смысл выражения обычно определяется контекстом и соблюдением правил математической нотации.

Для того чтобы определить, имеет ли выражение смысл в математике, можно провести следующие проверки:

1. Проверить синтаксическую корректность выражения. Выражение должно быть записано согласно правилам математической нотации, с использованием правильных символов и операторов.
2. Проверить, что выражение имеет определенное значение. Например, если выражение содержит переменные, нужно убедиться, что все переменные имеют значения, иначе выражение может быть неопределенным.
3. Проверить, что выражение не нарушает правила математических операций. Например, деление на ноль или извлечение корня из отрицательного числа являются недопустимыми операциями.

Примеры выражений, которые имеют смысл в математике:

• 2 + 3
• x + 5
• sin(π/2)
• √9

Примеры выражений, которые не имеют смысл в математике:

• 2 +
• x + y + z =
• 1/0
• √(-1)

Правильное понимание и интерпретация смысла выражения в математике играют важную роль в решении математических задач и формулировании математических теорем и законов.

Выражения, которые не имеют смысла в математике

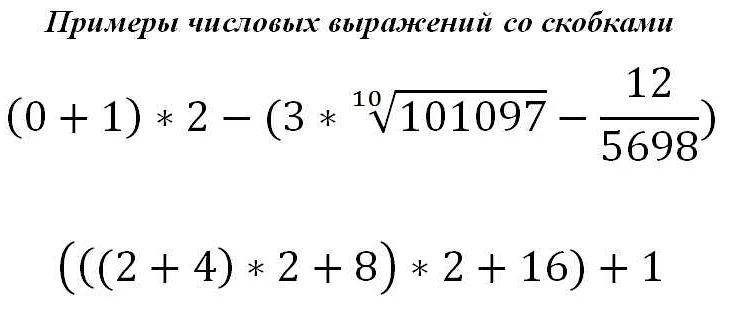
В математике существуют некоторые выражения, которые не имеют смысла и не могут быть вычислены. Это происходит по разным причинам, таким как нарушение математических правил, неопределенности или некорректность формулировок.

Некоторые примеры выражений, которые не имеют смысла:

1. Деление на ноль: выражение 1/0 не имеет смысла, так как невозможно разделить число на ноль. Результат подобного выражения неопределен и не может быть вычислен.

2. Извлечение корня из отрицательного числа: выражение √(-1) не имеет смысла в действительных числах, так как корень квадратный отрицательного числа не определен в этой области.

3. Некорректные формулировки: некоторые выражения могут быть синтаксически неправильными и не иметь смысла. Например, выражение 2 + или 3 * 5 +) являются некорректными и не могут быть вычислены.

Все эти примеры демонстрируют, что выражение должно быть корректно сформулировано и соответствовать математическим правилам, чтобы иметь смысл и быть вычисленным.

Какие последствия могут быть, если выражение не имеет смысла в математике

1. Недопустимые операции или операнды: Если выражение содержит операции или операнды, которые не определены или не согласуются с правилами математики, оно не имеет смысла. Например, деление на ноль или логарифм отрицательного числа.

2. Неопределенные значения: В некоторых случаях выражение может иметь неопределенное значение, например, при делении нуля на ноль. В таких случаях нельзя однозначно определить результат, и выражение не имеет смысла.

3. Противоречивые условия: Если условия задачи противоречивы или несовместимы, выражение может не иметь смысла. Например, если в задаче требуется найти квадратный корень отрицательного числа, это невозможно в рамках вещественной математики.

Если выражение не имеет смысла, это может привести к ошибкам в вычислениях, неверным выводам и некорректным решениям задач. Поэтому важно внимательно анализировать выражения и обращать внимание на их смысловую корректность.

Как использовать понятие «имеет смысл» в решении математических задач

Для использования понятия «имеет смысл» в решении математических задач, необходимо учесть следующие моменты:

1. Проверьте, что все переменные и значения, используемые в выражении, имеют определенное значение. Например, если в задаче говорится о количестве яблок, убедитесь, что вы знаете, сколько именно яблок есть.

2. Проверьте, что все операции и функции, применяемые в выражении, имеют смысл для заданных переменных и значений. Например, деление на ноль недопустимо, поэтому важно убедиться, что знаменатель не равен нулю.

3. Учтите ограничения и условия задачи. Некоторые математические операции, например, извлечение корня или логарифмирование, могут быть ограничены определенными значениями или требовать выполнения определенных условий.

4. Проверьте результат выражения на соответствие логике и реальности задачи. Например, если решением является отрицательное число, но в контексте задачи это невозможно, то выражение, вероятно, было неправильно составлено или решено.

Применение понятия «имеет смысл» в решении математических задач помогает избежать ошибок и неправильных результатов. Оно помогает убедиться, что решение является логичным, корректным и соответствует требованиям задачи. Поэтому важно всегда проводить проверку на наличие смысла в решении математических задач.

Вопрос-ответ:

Что означает выражение имеет смысл в математике?

В математике выражение имеет смысл, если оно может быть вычислено и дает конкретный результат.

Как определить, имеет ли выражение смысл?

Выражение имеет смысл, если все его переменные и операции определены и не приводят к неопределенным или некорректным значениям.

Какие примеры выражений, имеющих смысл в математике?

Примерами выражений, имеющих смысл в математике, являются: «2 + 3», «5 * x», «sin(x)», где переменные и операции определены и могут быть вычислены.

Что происходит, если выражение не имеет смысла в математике?

Если выражение не имеет смысла, то оно не может быть вычислено или дает неопределенный результат, что может привести к ошибкам в решении математических задач.

Какие проблемы могут возникнуть, если не учитывать смысл выражений в математике?

Если не учитывать смысл выражений, можно получить некорректные результаты, сделать ошибки в решении задач или неправильно интерпретировать математические модели.

Видео по теме: