Что такое дружественные числа в математике 5

Узнайте, что такое дружественные числа и как они связаны с математикой. Узнайте, какие числа считаются дружественными и как их можно найти. Познакомьтесь с примерами дружественных чисел и узнайте, зачем они важны в математике.

Дружественные числа – это особый тип чисел в математике, который является одним из самых интересных и загадочных явлений в этой науке. Дружественные числа представляют собой пары чисел, для которых сумма всех делителей первого числа (кроме самого числа) равна второму числу, а сумма всех делителей второго числа (кроме самого числа) равна первому числу.

Например, пара дружественных чисел (220, 284) является одной из самых известных. Делители числа 220 (кроме самого числа) – это числа 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 и 110. Их сумма равна 284, что является вторым числом в паре. Делители числа 284 (кроме самого числа) – это числа 1, 2, 4, 71 и 142. Их сумма равна 220, что является первым числом в паре.

История дружественных чисел началась ещё в Древней Греции, когда математик Пифагор (ок. 570 – ок. 495 г. до н.э.) изучал числа и отношения между ними. Однако, они получили своё название только в средние века, когда французский математик Амикаль Колла (1603-1662) впервые их описал и сформулировал основное определение.

Что такое дружественные числа?

Для примера, пара дружественных чисел 220 и 284. Делители числа 220 это 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 и 110. Их сумма равна 284. Делители числа 284 это 1, 2, 4, 71 и 142. Их сумма равна 220.

Дружественные числа представляют собой интересное явление в математике и до сих пор являются объектом исследований. Они были открыты еще в Древнем Египте, и изучаются до сегодняшнего дня.

Определение дружественных чисел

Например, пара чисел 220 и 284 являются дружественными. Делители числа 220 (кроме самого числа) — 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 и 110. Их сумма равна 284. Делители числа 284 (кроме самого числа) — 1, 2, 4, 71 и 142. Их сумма равна 220.

Такие пары чисел встречаются редко, и изначально были открыты древнегреческим математиком Пифагором. Дружественные числа являются одним из интересных феноменов в математике и до сих пор представляют определенный научный интерес.

Примеры дружественных чисел

Существует несколько известных примеров дружественных чисел. Одним из самых известных является пара чисел 220 и 284.

Первое числоВторое число

220

284

Для числа 220 сумма всех его делителей (кроме самого числа) равна 284:

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284

Для числа 284 сумма всех его делителей (кроме самого числа) равна 220:

1 + 2 + 4 + 71 + 142 = 220

Другим примером дружественных чисел является пара 1184 и 1210:

Первое числоВторое число

1184

1210

И так далее.

Свойства дружественных чисел

Дружественные числа обладают несколькими интересными свойствами:

СвойствоОписание

Сумма делителей	Сумма всех делителей первого числа равняется второму числу, а сумма всех делителей второго числа равняется первому числу.
Простые множители	Дружественные числа имеют одинаковые простые множители.
Сумма простых множителей	Сумма простых множителей первого числа равняется сумме простых множителей второго числа.
Отношение делителей	Дружественные числа имеют отношение, равное отношению суммы делителей к самому числу.

Из-за этих свойств, дружественные числа представляют интерес для математиков и используются в различных областях, включая теорию чисел и криптографию.

Сумма делителей числа

Для любого числа n существует конечное количество делителей, включая 1 и само число n. Например, для числа 6 делителями будут числа 1, 2, 3 и 6.

Чтобы найти сумму делителей числа, нужно сложить все эти делители. Например, для числа 6 сумма делителей будет равна 1 + 2 + 3 + 6 = 12.

Сумма делителей числа может быть полезна при решении различных задач, связанных с числами. Например, она может использоваться для определения дружественных чисел, которые являются парами чисел, сумма делителей каждого из которых равна другому числу.

Также сумма делителей числа может использоваться для определения совершенных чисел, которые являются такими числами, сумма делителей которых равна самому числу.

Зная сумму делителей числа, можно также определить, является ли оно простым числом, так как у простых чисел сумма делителей равна 1 + число.

Используя понятие суммы делителей числа, можно решать различные задачи, связанные с делителями, кратностью и другими арифметическими свойствами чисел.

Связь с совершенными числами

Существует тесная связь между дружественными числами и совершенными числами. Если два числа являются дружественными, то их сумма также является совершенным числом. Например, пара дружественных чисел (220, 284) имеет сумму 504, которая является совершенным числом.

Это связано с тем, что каждое дружественное число является суммой всех своих делителей, исключая само число. Когда два дружественных числа складываются, каждый делитель одного числа также является делителем второго числа, и наоборот. Поэтому сумма делителей обоих чисел будет равной сумме делителей суммы этих чисел.

Совершенные числа и дружественные числа являются интересными объектами исследований в математике. Их свойства и особенности продолжают вызывать ученых и математиков большой интерес.

Дружественные числаСовершенные числа

220, 284	6, 28
1184, 1210	496
2620, 2924	8128

История и интересные факты о дружественных числах

Дружественные числа — это пары натуральных чисел, для которых сумма всех делителей первого числа (кроме самого числа) равна второму числу, а сумма всех делителей второго числа (кроме самого числа) равна первому числу. Например, пара чисел (220, 284) является дружественными числами, так как сумма всех делителей 220 равна 284, а сумма всех делителей 284 равна 220.

Интересно отметить, что первые дружественные числа были открыты еще в древности. Древние египтяне и ассирийцы знали о некоторых дружественных числах и использовали их в своих математических расчетах.

Однако, настоящий интерес к дружественным числам возник в эпоху Возрождения, когда ученые начали проводить более глубокие исследования в области числовых последовательностей. Одним из важных открытий было то, что дружественные числа можно представить в виде цепочки, включающей большее количество чисел.

С течением времени были найдены множество пар дружественных чисел. Некоторые из них имеют очень большие значения. Например, самая большая известная пара дружественных чисел (состоящая из 2 052 585 941 552 441 701 и 2 111 365 626 041 035 705) была найдена в 2012 году.

Дружественные числа по-прежнему остаются объектом интереса для математиков. Их изучение помогает ученым лучше понять природу чисел и их взаимосвязь. Кроме того, дружественные числа имеют важное практическое применение в криптографии и других областях науки.

• Дружественные числа обладают рядом интересных свойств и закономерностей.
• Существуют различные методы и алгоритмы для поиска дружественных чисел.
• Дружественные числа являются основой для создания некоторых математических задач и головоломок.

Итак, дружественные числа представляют собой интересное и увлекательное явление в математике, которое продолжает вызывать интерес исследователей. Их изучение помогает расширить наши знания о числах и их свойствах, а также находит применение в различных областях науки и техники.

Видео по теме:

Вопрос-ответ:

Что такое дружественные числа в математике?

Дружественные числа в математике — это пары или группы чисел, для которых сумма делителей одного числа равна другому числу и наоборот. То есть, сумма всех делителей первого числа равна второму числу, а сумма всех делителей второго числа равна первому числу.

Какие существуют примеры дружественных чисел?

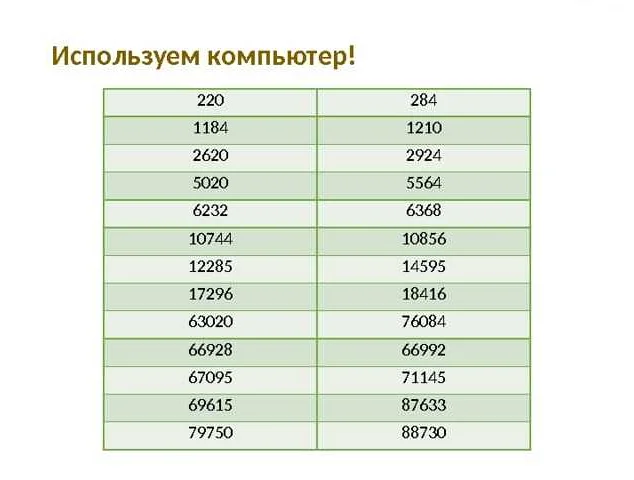
Несколько примеров дружественных чисел: (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368). Все эти пары чисел являются дружественными, потому что сумма всех делителей первого числа равна второму числу, и наоборот.

Какую роль играют дружественные числа в математике?

Дружественные числа являются одним из интересных объектов изучения в математике. Они помогают углубить понимание теории чисел, а также применяются в различных алгоритмах и задачах, связанных с нахождением и анализом делителей чисел.

Кто открыл и изучал дружественные числа?

Понятие дружественных чисел было открыто и изучено древнегреческими математиками. Один из первых упоминаний о дружественных числах можно найти у Пифагора, который жил в 6-5 веках до н.э. Однако, более детальное исследование этой темы началось в 18-19 веках, когда математики начали систематически искать и изучать дружественные числа.

Существуют ли дружественные числа с более чем двумя числами в паре?

Да, помимо пар дружественных чисел существуют также группы дружественных чисел, состоящие из трех и более чисел. Например, существует группа дружественных чисел (220, 284, 1184, 1210), где сумма всех делителей каждого числа равна сумме делителей других чисел в группе.

Значение и применение дружественных чисел в математике

Дружественные числа имеют различные применения в математике. Они используются в различных алгоритмах и задачах, а также являются объектом исследования в теории чисел.

Одним из применений дружественных чисел является задача нахождения совершенных чисел. Совершенное число — это число, равное сумме всех своих делителей, не включая само число. Именно с помощью дружественных чисел можно строить совершенные числа. Например, если (220, 284) — дружественная пара чисел, то 220 + 284 = 504, и 504 является совершенным числом.

В математике также изучаются свойства дружественных чисел. Например, известно, что сумма всех делителей числа является мультипликативной функцией, то есть f(ab) = f(a) * f(b), если числа a и b взаимно простые. Дружественные числа приводят к интересным результатам при применении таких функций.

Кроме того, дружественные числа используются в криптографии. Например, они могут быть использованы при генерации ключей для шифрования информации. Использование дружественных чисел в криптографии позволяет создать более надежные и сложные системы защиты данных.

Таким образом, дружественные числа имеют значительное значение и находят применение в различных областях математики, начиная от задач нахождения совершенных чисел и исследования свойств чисел, и заканчивая криптографией.

Криптография и дружественные числа

Одно из применений дружественных чисел в криптографии — использование их в криптографических хэш-функциях. Хэш-функция — это функция, которая преобразует входные данные в уникальный набор битов, называемый хэш-значением. Хэш-функции широко используются для проверки целостности данных и создания цифровых подписей.

Дружественные числа могут использоваться в качестве исходных данных для хэш-функции, чтобы создать уникальные хэш-значения. Например, можно использовать сумму делителей дружественного числа в качестве входных данных для хэш-функции. Это позволяет создавать различные хэш-значения для разных дружественных чисел, что повышает безопасность системы.

Кроме того, дружественные числа могут использоваться в алгоритмах шифрования для создания ключей шифрования. Ключ шифрования — это уникальная последовательность символов, которая используется для преобразования данных в зашифрованный вид. Использование дружественных чисел в качестве ключей шифрования может повысить безопасность шифрования и усложнить взлом системы.

Таким образом, дружественные числа имеют важное значение в криптографии и могут быть использованы для защиты информации. Использование этих чисел в хэш-функциях и алгоритмах шифрования может помочь создать безопасные системы и защитить данные от несанкционированного доступа.