Характер зависимости в математике: основные понятия и примеры

Характер зависимости в математике — это связь между двумя или более переменными, которая может быть линейной, нелинейной, прямой или обратной. Знание характера зависимости позволяет делать выводы о природе этих переменных и использовать их для прогнозирования будущих значений.

Зависимость – это явление, которое существует во всех сферах жизни и достаточно часто используется в математике. Она определяется как изменение одной величины при изменении другой. Характер зависимости в математике определяется тем, как одна величина воздействует на другую.

В математике характер зависимости может быть функциональной или статистической. Функциональная зависимость проявляется в том, что одна величина имеет непосредственное влияние на другую. Примерами могут служить функции вида y = f(x), где y зависит от x.

Статистическая зависимость, в свою очередь, проявляется в том, что изменения одной величины вызывают изменения другой, но не обязательно напрямую. Например, при анализе данных о продажах автомобилей, можно установить зависимость между ценой и объемом продаж, хотя сама цена не играет прямой роли в объеме продаж.

В данной статье мы рассмотрим примеры различных характеров зависимостей в математике, а также расскажем об их особенностях.

Что такое характер зависимости?

Характер зависимости в математике — это свойство отношения между двумя переменными, которое определяет, как изменения одной переменной влияют на другую. Он может быть линейным, квадратичным, абсолютным, обратным, однозначным или многозначным.

Линейная зависимость означает, что при изменении одной переменной на определенную величину, другая переменная изменится на постоянное значение, умноженное на эту величину. Квадратичная зависимость означает, что изменения одной переменной могут приводить к более значительным изменениям другой переменной.

Абсолютная зависимость находится, когда одна переменная полностью определяет значение другой переменной, а обратная зависимость возникает, когда изменение одной переменной приводит к изменению другой переменной в противоположном направлении. Однозначная зависимость означает, что каждому значению одной переменной соответствует единственное значение другой переменной, а многозначная зависимость означает, что каждому значению одной переменной может соответствовать несколько значений другой переменной.

Характер зависимости имеет важное значение в многих областях математики и науки. Он помогает прогнозировать изменения в системах, оптимизировать процессы и разрабатывать математические модели. Поэтому важно понимать, как он работает и как его можно применять в практических целях.

Какие бывают виды характера зависимости и их основные черты?

Прямая зависимость — это тип зависимости, при котором увеличение одной переменной приводит к увеличению другой. Примером прямой зависимости может служить зависимость количества пройденных километров от количества израсходованного топлива.

Обратная зависимость — это тип зависимости, при котором увеличение одной переменной приводит к уменьшению другой. Примером обратной зависимости может служить зависимость времени ожидания автобуса от числа человек на остановке.

Линейная зависимость — это тип зависимости, основанный на линейной функции. При линейной зависимости изменение одной переменной приводит к изменению другой переменной в равной степени. Примеры линейной зависимости включают зависимость цены на автомобиль от его пробега или зависимость количества продаж от объема рекламы.

Нелинейная зависимость — это тип зависимости, в которой связь между переменными не может быть представлена линейной функцией. Примером нелинейной зависимости может служить зависимость скорости сигнала в зависимости от длины волны.

Экспоненциальная зависимость — это тип нелинейной зависимости, при которой изменение одной переменной приводит к экспоненциальному изменению другой переменной. Пример экспоненциальной зависимости может служить зависимость числа бактерий в зависимости от времени.

Логарифмическая зависимость — это тип нелинейной зависимости, при которой одно из значений обратно пропорционально логарифму другого. Примером логарифмической зависимости может служить зависимость количества времени, необходимого для выполнения задачи, от размера задачи.

Степенная зависимость — это тип нелинейной зависимости, при которой одно значение изменяется в степенной зависимости от другого. Пример степенной зависимости может служить поверхностное натяжение жидкости в зависимости от ее объема.

Примеры характеров зависимости в математике

Зависимость — это связь между двумя или более величинами. В математике существуют различные типы зависимости, которые могут проявляться в графиках и уравнениях.

Линейная зависимость: это прямая линия, которая проходит через две точки на графике. Линейная зависимость обычно описывается уравнением y = mx + b, где y — зависимая переменная, x — независимая переменная, m — наклон прямой и b — точка пересечения с осью y.

Квадратичная зависимость: это парабола, которая выводится из уравнения y = ax² + bx + c, где a не равно 0. На графике это выглядит как изогнутая линия, которая может быть направлена вверх или вниз в зависимости от знака параметра a.

Обратно пропорциональная зависимость: это зависимость между двумя величинами, где одна величина увеличивается, а другая уменьшается. Эту зависимость можно описать формулой y = k/x. На графике это может быть гипербола, которая состоит из двух ветвей.

Пропорциональная зависимость: это зависимость между двумя величинами, где одна величина изменяется пропорционально другой. Эта зависимость может быть описана уравнением y = kx, где k — постоянный множитель. На графике это будет прямая линия, которая проходит через начало координат.

Возможно, эти примеры характеров зависимости помогут вам лучше понять, как различные величины в математике могут быть связаны между собой.

Как определить характер зависимости в математической модели?

Характер зависимости в математической модели — это показатель того, как изменение одной переменной влияет на изменение другой переменной. Имеется в виду, что всякий раз, когда значение одной переменной меняется, значение другой переменной также меняется. Кроме того, в зависимости могут входить самые разные математические функции — линейные, квадратичные, экспоненциальные и т.д.

Для того чтобы определить характер зависимости, нужно провести анализ данных, определить, какие переменные связаны между собой, и построить графики и графики зависимости. При этом необходимо учесть, что разные типы зависимости могут предполагать разные способы анализа данных.

Например, в линейной зависимости график будет представлять собой прямую линию, а в экспоненциальной зависимости — кривую, которая начинается с небольшого значения, а затем стремительно растет.

Важно также помнить, что характер зависимости может изменяться в зависимости от изменения параметров модели. Поэтому для получения точных результатов следует проводить анализ данных на разных уровнях параметров, чтобы убедиться в том, что выбранный характер зависимости действительно корректен и актуален для рассматриваемой модели.

В целом, определение характера зависимости в математической модели служит необходимым и важным шагом для того, чтобы точно описать взаимосвязь между различными переменными и получить нужные результаты и выводы на основе математических расчетов.

Какие особенности характеризуют зависимость в математике?

Одной из основных особенностей зависимости в математике является то, что она является взаимосвязью между двумя или более переменными. Одна переменная зависит от другой, то есть изменения одной переменной вызывают изменения другой переменной.

Важной особенностью зависимости в математике является то, что она может быть представлена в виде графика или формулы. График зависимости позволяет визуализировать изменения переменных, а формула описывает точную математическую связь между ними.

Кроме того, зависимость может быть линейной или нелинейной. Линейная зависимость означает, что изменения переменных происходят пропорционально друг другу, тогда как в нелинейной зависимости это соотношение более сложное.

Наконец, стоит отметить, что зависимость может быть прямой или обратной. Прямая зависимость означает, что при увеличении одной переменной, увеличивается и другая переменная. В обратной зависимости наоборот — увеличение одной переменной приводит к уменьшению другой переменной.

Понимание особенностей зависимости в математике важно для понимания и решения ряда задач в науке, технике и экономике.

Зачем нужно знать о характере зависимости?

Математика и ее применение в реальной жизни

Характер зависимости используется для описания отношения между двумя переменными в математике. Знание о характере зависимости может помочь в правильном анализе данных и предсказании будущих значений. Поэтому, понимание данной темы необходимо не только для математиков, но и для всех, кто работает с данными, включая экономистов, социологов, физиков, и многих других.

Правильный выбор модели зависимости

Знание характера зависимости между переменными помогает выбрать правильную модель для ее описания. Например, если зависимость является линейной, то модель линейной регрессии вероятнее всего будет работать лучше всего, чем другие модели. Однако, если зависимость является нелинейной, то линейная модель может дать неточные результаты. Поэтому, знание о характере зависимости между переменными помогает выбрать наиболее подходящую модель и получить более точные результаты.

Предотвращение ошибок в анализе данных

Неправильный анализ данных может привести к неверным выводам. Знание о характере зависимости помогает избежать типичных ошибок при анализе данных, такие как интерпретация линейной зависимости как нелинейной и наоборот. В конечном итоге, знание о характере зависимости улучшит качество анализа данных и позволит сделать верные выводы.

Какие приложения имеют характеры зависимости в математике?

Математика является одним из базовых наук и имеет широкое применение в различных областях, где ее характеристики и зависимости могут использоваться для решения задач и улучшения процессов.

Один из примеров зависимости в математике, который широко используется во многих областях, это линейная зависимость. Она проявляется в случаях, когда изменение одной величины приводит к пропорциональному изменению другой величины. Например, это может использоваться при расчете стоимости продукции в зависимости от количества используемых материалов.

Еще одним примером зависимости в математике является статистическая зависимость. Она имеет широкое применение в анализе данных и позволяет определить связь между двумя или более переменными. Например, это может использоваться для анализа влияния различных факторов на продажи товаров.

Кроме того, математические модели зависимости могут использоваться в физике, экономике, инженерии, биологии и других областях. Например, в физике математические зависимости могут использоваться для описания движения тел и решения задач механики. В экономике и бизнесе они могут использоваться для прогнозирования рыночных тенденций и анализа финансовых показателей.

Таким образом, математические зависимости имеют широкое применение в различных областях, где их можно использовать для решения различных проблем и задач.

Какие методы можно использовать для измерения характера зависимости?

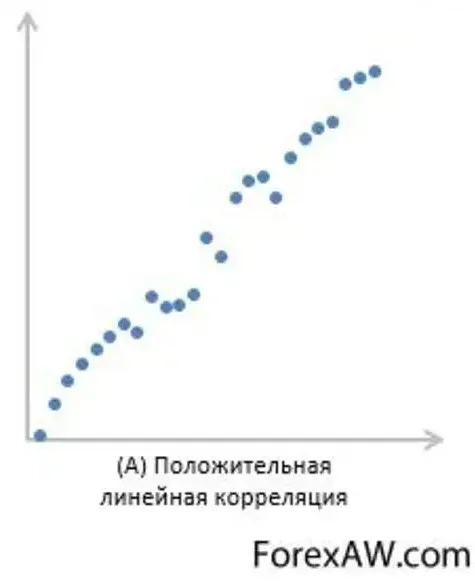
Для измерения характера зависимости в математике используют разные методы. Одним из наиболее распространенных методов является корреляционный анализ.

В рамках корреляционного анализа проверяют, какая связь существует между двумя переменными. Для этого используют корреляционный коэффициент, который может принимать значение от -1 до 1.

Также для измерения характера зависимости часто используется метод наименьших квадратов. Этот метод позволяет найти прямую или кривую, которая наилучшим образом описывает зависимость между двумя переменными.

Для более сложных зависимостей может использоваться регрессионный анализ. В этом случае исследователь определяет, как одна или несколько независимых переменных влияют на зависимую переменную. Рассчитываются коэффициенты регрессии, которые позволяют предсказывать значения зависимой переменной в зависимости от значений независимых переменных.

Важно выбрать подходящий метод для конкретного типа данных и зависимости, чтобы получить точные и корректные результаты.

• • Ключевые методы измерения характера зависимости:
    1. Корреляционный анализ
    2. Метод наименьших квадратов
    3. Регрессионный анализ

Какие особенности характеризуют нелинейные характеры зависимости?

В отличие от линейной зависимости, нелинейные зависимости между переменными могут быть более сложными и разнообразными:

• • • Нелинейные зависимости могут иметь различную форму: квадратичную, экспоненциальную, логарифмическую и многие другие.
    • Зависимости могут быть монотонно возрастающими или убывающими, иметь экстремумы или точки перегиба.
    • На графиках нелинейные зависимости могут проявляться в виде кривых, петель или других нестандартных форм.
    • Характер зависимости может быть определен только на основе анализа эмпирических данных или математической модели.

Кроме того, нелинейные зависимости часто проявляют сильную чувствительность к начальным условиям и параметрам модели. Это может приводить к неожиданным результатам и затруднять прогнозирование поведения системы в будущем.

Однако нелинейные зависимости могут быть также более точными и реалистичными, чем линейные, особенно в случае сложных систем и процессов. Поэтому исследование нелинейных зависимостей остается актуальной и важной задачей в математике и ее приложениях.

Какие проблемы могут возникнуть при анализе характера зависимости?

Недостаточность данных: Одной из основных проблем при анализе характера зависимости является недостаточность данных. Если данные оказались неполными, то анализ зависимости может дать неточные результаты, что может привести к неправильным выводам.

Несоответствие факторов: Иногда анализ характера зависимости может столкнуться с проблемой несоответствия факторов. Например, при анализе зависимости между личностью и успехом в карьере нельзя игнорировать другие факторы, такие как возраст, образование, опыт работы и т.д.

Слабая связь: Иногда связь между двумя переменными может быть очень слабой, что делает ее трудно определить. В этом случае необходимо использовать статистические методы для определения связи между переменными.

Обратные зависимости: Принимая во внимание только прямые связи при анализе характера зависимости, можно упустить возможность существования обратной зависимости. Это такая связь, при которой изменение одной переменной приводит к обратному изменению другой переменной.

Выбросы: Выбросы являются еще одной проблемой в анализе характера зависимости. Их наличие может исказить результаты анализа, и поэтому желательно удалить их из набора данных перед проведением анализа.

Какие перспективы развития изучения характера зависимости в математике?

Современная математика находится в постоянном развитии, и изучение характера зависимости является одной из ключевых областей.

Одним из направлений развития изучения характера зависимости является применение машинного обучения и анализа данных. С помощью этих методов можно выявлять закономерности и зависимости в больших объемах данных, что помогает решать задачи в различных областях, например, в экономике и медицине.

Другим перспективным направлением является исследование нелинейных зависимостей и разработка новых методов их анализа. Нелинейные зависимости встречаются в разных областях математики и физики, и их изучение помогает понимать и объяснять различные явления и процессы.

Также важно развивать теорию вероятностей и статистики, которые являются основой для анализа зависимостей и предсказания будущих значений. Новые методы и подходы к анализу статистических данных помогают улучшать качество прогнозов и принимать более обоснованные решения.

В целом, изучение характера зависимости остается важной областью математики, и ее развитие помогает решать множество прикладных задач.

Вопрос-ответ:

Что такое характер зависимости в математике?

Характер зависимости – это связь между двумя переменными, которая может быть представлена графиком, уравнением или таблицей значений.

Как определить характер зависимости?

Характер зависимости можно определить по форме графика или уравнения функции. Для линейной зависимости график будет прямой, а уравнение иметь вид y = kx + b. Для параболической зависимости график будет параболой, а уравнение иметь вид y = ax² + bx + c.

Какие бывают типы характера зависимости в математике?

Бывают линейная, параболическая, гиперболическая, экспоненциальная, логарифмическая зависимости.

Какие особенности имеет характер зависимости в математике?

Особенностью характера зависимости является то, что он может быть представлен в виде графика или уравнения, что позволяет установить связь между двумя переменными. Кроме того, характер зависимости может быть использован для прогнозирования изменений в переменной.

Какие примеры характера зависимости в математике?

Примерами характера зависимости в математике могут служить: зависимость цены на продукты от количества покупателей; скорость движения автомобиля от времени; высота полета ракеты от времени.

Какие еще применения может иметь характер зависимости в математике?

Характер зависимости может быть использован для прогнозирования изменений в переменной, а также для определения максимального или минимального значения функции. Кроме того, он может быть использован в рамках экономических и физических исследований для определения закономерностей и принятия решений в бизнесе и науке.

Какова роль характера зависимости в математике?

Характер зависимости играет важную роль в математике, так как позволяет установить связь между двумя переменными и прогнозировать изменения в переменной. Это важно для принятия решений в бизнесе и науке, а также для проведения экономических и физических исследований.

Видео по теме: