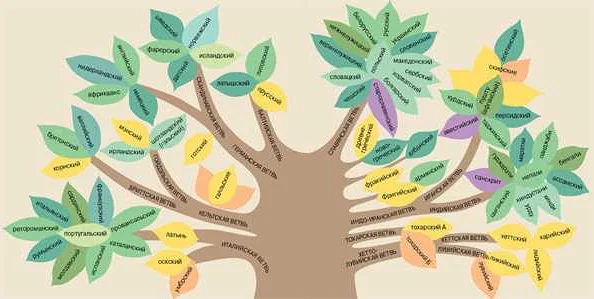
История применения математических моделей в лингвистике: первые шаги и достижения

Статья расскажет о том, кто впервые начал применять математические модели в лингвистике. Изучите историю применения математических методов в языковых исследованиях и познакомьтесь с первопроходцами этой области науки.

Современная лингвистика исходит из традиции структурализма, который рассматривал язык как систему, в которой различные элементы играют свои определенные роли. В 50-х годах XX века на полях лингвистического структурализма начали появляться исследования, основанные на математических моделях и методах.

Идея применения математики в лингвистике была не новой — она возникла еще в XIX веке. Однако, ранние попытки построения математических моделей языка не были особо успешными, т.к. отсутствовали соответствующие математические инструменты. С развитием компьютерной техники, появились электронные датчики и быстродействующие машины, что дало возможность создать более совершенные модели.

Одним из первых, кто принес математику в лингвистику, стал американский лингвист Джордж Керни. Он разработал математическую модель для анализа морфологической структуры языка. В своих работах он применял теорию категорий, теорию автоматов и другие математические инструменты. В последствии, эта модель была усовершенствована и развита современными лингвистами.

Роль математики в изучении языка

Математические методы и модели находят своё применение в огромном количестве областей науки и техники. Они также могут быть весьма полезными в изучении языка. В современной лингвистике математика используется для построения формальных моделей, которые могут помочь в создании компьютерных программ для автоматического перевода языков, определения стиля текста и даже анализа структуры грамматики.

В древности математика выступала в качестве помощника в изучении лингвистики. Греческие философы, такие как Платон и Аристотель, были убеждены в том, что с помощью математических методов можно научиться понимать язык и построить строгое логическое мышление.

Математика в языковых исследованиях нашла своё применение благодаря Клоду Шенону, который в 1948 году опубликовал статью «Математическая теория связи», в которой широко использовался термин «информация». Он разработал математическую модель языка на основе теории информации. Шенон доказал, что язык является источником информации, а его бессмысленный шум — источником энтропии.

С появлением компьютерных технологий, математические методы в лингвистике стали ещё более востребованными. С помощью алгоритмов, основанных на математических моделях, можно улучшить качество машинного перевода, что очень важно в мире, где все больше и больше людей сталкиваются с необходимостью общаться на разных языках.

Первые шаги к созданию математических моделей языка

В начале XX века появилась идея создания математических моделей языка. Одним из первых ученых, занявшихся этим вопросом, был лингвист Леонард Блумфилд. В своих работах он пытался создать формальные описания языковых явлений на основе математических методов и уравнений. Он считал, что язык можно рассматривать как систему символов и правил для их сочетания, которые можно описать с помощью математических символов и уравнений.

Другим из первых, кому удалось применить математику в лингвистике, был американский математик Уоррен Уивер. В 1949 году он опубликовал статью, в которой предложил использовать математическую теорию информации для анализа текстов. Он пытался показать, что любой язык можно рассматривать как систему, которая передает информацию, и что можно использовать математические методы для определения того, насколько эффективно передается эта информация.

В 50-х годах XX века идеи Блумфилда и Уивера получили продолжение от других лингвистов. В частности, Ноам Хомский развил теорию грамматики, которая позволила формально описывать языки на основе набора правил для их построения. Он использовал при этом математические символы и уравнения, чтобы формализовать свои идеи. Кроме того, лингвисты начали применять компьютеры для анализа языка с помощью математических методов.

В целом, первые шаги к созданию математических моделей языка были сделаны в первой половине XX века, когда лингвисты начали применять математические методы для описания языковых явлений. Этот подход показал свою эффективность и позволил существенно расширить наши знания о языке. Сегодня математические методы используются в лингвистике очень широко, и они стали неотъемлемой частью этой науки.

Теория автоматов и математические модели языковой структуры

В развитии лингвистических исследований теория автоматов занимает значительное место. Она была разработана в 40-х годах XX века математиками Хаутоном, Шмилевицем и Мура, и представляет собой формально-математическую теорию моделей, использующих автоматы для описания процессов принятия решений.

Применение теории автоматов в лингвистике позволило создать математические модели языковых структур и алгоритмы их распознавания и генерации. Так, например, контекстно-свободные грамматики описываются через четверки, состоящие из множества нетерминальных символов, множества терминальных символов, начального символа и набора правил вывода. В свою очередь, разложение грамматики на составляющие часто описывается при помощи рекурсивных функций и алгоритма Коки.

Среди разработчиков первых математических моделей языковой структуры можно выделить Н. Хомского, который в своей знаменитой книге «Синтаксические структуры» сформулировал теорию языкового анализа на основе формальных грамматик.

Сегодня теория автоматов и математические модели языковой структуры являются важным инструментом для разработки и оптимизации компьютерных программ, использующих естественный язык. Они находят свое применение в области машинного перевода, в задачах распознавания и синтеза речи, а также в других областях, связанных с анализом и обработкой текста.

Корпусные исследования и статистические методы в лингвистике

Корпусные исследования – это методология исследования языка, которая основывается на анализе больших объемов текстового материала – корпусов. Корпус состоит из текстов, собранных из различных источников и представляет собой множество примеров естественного языка. В лингвистике корпусные исследования активно используются для изучения различных языковых явлений, таких как лексика, грамматика, стилистика и др.

Для обработки длинных списков слов, их исследования и сравнения статистические методы в лингвистике тоже получили широкое применение. Они позволяют измерять частотность слов, анализировать распределение слов по текстам и находить общие закономерности в языке. С помощью статистических методов можно выявлять различия в использовании слов в разных организациях, культурах и обществах. Такие исследования позволяют лучше понимать происхождение языковых явлений и структуру языка.

Современные методы корпусных исследований и статистического анализа помогают лингвистам получить более точные и объективные результаты, а также обеспечивают уникальную возможность для сравнительного анализа различных языков и текстов.

Исследования в области семантики на математической основе

В исследованиях в области семантики на математической основе используются математические модели для описания языковых явлений и обобщений. Это позволяет установить закономерности и принципы функционирования языковых систем.

Одной из таких моделей является семантическая сеть, где слова представлены узлами, а связи между ними – ребрами. Она используется для описания значений слов и их отношений в различных контекстах. С помощью семантической сети можно выявить семантические поля, а также проанализировать сходства и различия между словами.

Еще одной моделью, используемой в семантике, является лексическая семантика, которая основывается на теории групп значений. С помощью этой модели можно анализировать значение слова в зависимости от его контекста.

Также в исследованиях семантики применяются вероятностные модели, которые позволяют определить вероятность появления тех или иных слов и установить зависимости между словами на основе их частотности в текстах.

Исследования в области семантики на математической основе позволяют более глубоко понимать языковые явления. Математические методы дополняют и расширяют классические лингвистические методы и создают новые возможности для анализа и описания языков.

Формализация синтаксических правил языка и использование формальных грамматик

С развитием лингвистики возникла необходимость формализовать правила грамматики языка для их более точного описания и анализа. Для этого были использованы формальные грамматики – системы правил, описывающие все возможные комбинации слов и выражений в языке.

Одной из первых формальных грамматик была контекстно-свободная грамматика, разработанная в 1956 году Н. Хомским. Она описывает составление предложений из лексических единиц и синтаксических правил, очерчивая возможные деревья разбора для каждой конструкции.

В лингвистике применения формальных грамматик связаны с исследованием синтаксической структуры языка, а также автоматическим анализом текстов, например, в машинном переводе или при распознавании речи. Использование формальных грамматик позволяет более точно определить синтаксическую структуру предложений, что в свою очередь помогает в создании более эффективных методов анализа текстов.

Сегодня существует несколько разных видов формальных грамматик, наиболее популярными из которых являются контекстно-свободные и регулярные грамматики. Каждая грамматика предназначена для решения определенных задач в лингвистике и компьютерных науках.

Использование формальных грамматик в лингвистике продолжает активно развиваться и находит все большее применение в создании интеллектуальных систем обработки и анализа языка.

Интеллектуальные системы и искусственный интеллект в лингвистике

В современном мире искусственный интеллект используется в различных сферах, включая лингвистику. Интеллектуальные системы могут помочь в анализе, обработке и понимании языка.

Одно из применений искусственного интеллекта в лингвистике — создание систем машинного перевода. Системы машинного перевода используют компьютерные алгоритмы и модели, чтобы перевести тексты с одного языка на другой. Эти системы также используются для анализа текстов на других языках, что помогает сделать лингвистические исследования более междисциплинарными.

Искусственный интеллект также может использоваться для создания систем автоматической распознавания речи. Эти системы позволяют компьютерам транскрибировать звуковую речь в текст, а также анализировать и классифицировать такие параметры, как интонация и эмоциональный тон.

Также одним из применений искусственного интеллекта в лингвистике является анализ больших данных. Интеллектуальные системы могут быстро обрабатывать большие объемы текстовой информации, что позволяет выявлять тенденции и закономерности в языке.

В целом, использование искусственного интеллекта в лингвистике может помочь улучшить наше понимание языка и сделать лингвистические исследования более точными и систематизированными.

Математические методы в компьютерной лингвистике

Компьютерная лингвистика — это научная область, которая занимается созданием компьютерных программ, способных обрабатывать естественный язык, а также анализом языковых данных. Математические методы широко используются в компьютерной лингвистике для создания эффективных алгоритмов и моделей для обработки и анализа языковых данных.

В компьютерной лингвистике используются различные математические методы, такие как линейная алгебра, статистика, теория вероятностей, теория графов, теория категорий и многие другие. Эти методы используются для разработки алгоритмов машинного обучения, обработки текстов, анализа эмоциональной окраски текстов, морфологического и синтаксического анализа, анализа семантики и много других задач.

Важным примером использования математических методов в компьютерной лингвистике является создание моделей языка. Моделируя язык с помощью математических методов, можно определить частоту использования слов, выделить грамматические правила и закономерности, а также определить синонимы и антонимы.

Кроме того, в компьютерной лингвистике широко используются методы машинного обучения, такие как нейронные сети, генетические алгоритмы, деревья решений и многие другие. Эти методы позволяют создавать програмные системы, способные распознавать, интерпретировать и генерировать естественный язык.

Таким образом, математические методы играют важную роль в компьютерной лингвистике. С их помощью создаются эффективные алгоритмы и модели для обработки, анализа и генерации естественного языка, что является важным шагом в развитии компьютерной технологии и коммуникации человека и компьютера.

Использование предикатной логики для анализа языковых конструкций

Предикатная логика – это логическая система, которая используется для формального описания отношений между объектами и явлениями в различных науках, включая лингвистику. Эта система позволяет выражать сложные конструкции языка в виде формальных утверждений, что делает их более доступными для дальнейшего анализа и обработки.

В рамках лингвистики, предикатная логика используется для анализа множества языковых конструкций. Например, она позволяет формализовать отношения между субъектом, глаголом и объектом предложения, что дает возможность лучше понять их смысловое значение и взаимосвязь.

Более того, предикатная логика может быть использована для формализации различных типов отношений и конструкций в языке, таких как отрицание, вопросительные предложения, модальные глаголы и многое другое. Это открывает новые возможности для анализа и понимания языка, а также для создания различных языковых моделей.

Таким образом, использование предикатной логики для анализа языковых конструкций представляет собой эффективный и перспективный подход к исследованию языковых феноменов, который уже привел к созданию множества новых исследовательских методов и моделей в лингвистике.

Нейронные сети и их применение в лингвистике

Нейронные сети – это алгоритмы машинного обучения, которые моделируют работу человеческих нейронов. Они позволяют создавать сложные модели, позволяющие машинам производить сложные задачи, такие как обработка изображений, распознавание речи или классификация текстов.

В лингвистике нейронные сети играют важную роль. Они используются, например, для распознавания речи и создания синтеза речи, и для обработки естественного языка и классификации текстов. Например, с помощью нейронных сетей можно обучить компьютер распознавать и классифицировать тексты на разные темы, определять тональность текста или авторство текста.

Нейронные сети также позволяют создавать модели, которые могут выделять ключевые слова, интерпретировать смысл предложений и анализировать тексты на предмет структуры, грамматики и лексики. Эти функции очень важны в лингвистике, так как они помогают улучшить качество машинного перевода, создания семантических баз данных и анализа больших массивов текстовых данных.

Несмотря на свои преимущества, нейронные сети также имеют свои ограничения и сложности. Например, они могут требовать больших объемов данных для обучения и могут быть чувствительны к шуму и некоторым видам ошибок. Важно проводить дополнительные исследования и эксперименты, чтобы улучшить качество работы нейронных сетей в лингвистике и получить более точные результаты и выводы.

Современные математические подходы в лингвистике: достижения и перспективы

С развитием вычислительных технологий и компьютерных наук, лингвистика получила новые возможности применения математических методов в своих исследованиях. Современные математические подходы в лингвистике позволяют решать широкий круг задач, начиная от анализа текстов и определения языковых закономерностей, заканчивая созданием искусственного интеллекта.

Одним из ярких достижений современной лингвистики является разработка компьютерных моделей естественного языка. Эти модели позволяют компьютеру обработать и понять естественный язык человека, выполнять задачи автоматического перевода текстов и создавать голосовых помощников на естественном языке.

Также в современной лингвистике активно применяются методы машинного обучения и статистического анализа текстов. Эти методы позволяют автоматически извлекать информацию из больших текстовых корпусов и находить скрытые структуры в языке.

В перспективе, математические подходы в лингвистике будут развиваться дальше, создавая новые инструменты для анализа языка и создания искусственного интеллекта, который сможет понимать и генерировать естественный язык. Это открывает новые горизонты для коммуникации между человеком и компьютером, а также для применения лингвистических исследований в других областях, например, в философии, психологии и социологии.

Вопрос-ответ:

Какие математические модели использовали в исследованиях первые лингвисты?

Первые лингвисты использовали статистические модели, основанные на анализе частотности встречаемости слов в текстах. Например, Андре Шляйхер в своих исследованиях использовал «метод сравнения частот».

Какие достижения были получены с помощью математических моделей в лингвистике?

С помощью математических моделей в лингвистике были получены многочисленные достижения, включая раскрытие закономерностей в языке, разработку новых методов анализа текстов, создание компьютерных моделей перевода и многое другое.

Кто из первых лингвистов занимался исследованиями по использованию математических моделей в лингвистике?

Среди первых лингвистов, которые занимались исследованием использования математических моделей в лингвистике, можно отметить Андре Шляйхера, З. Г. Харкевич, Ж. С. Фуркад, Р. М. Суслов и др.

Какие методы использовались для анализа текстов с помощью математических моделей?

Для анализа текстов с помощью математических моделей использовались такие методы, как анализ частотности слов, построение фонетических моделей, использование статистических методов и другие.

Какие преимущества имеют математические модели в сравнении с традиционными лингвистическими методами?

Математические модели позволяют более точно и объективно проанализировать языковые данные, выявить закономерности, которые могли бы быть упущены при традиционных лингвистических методах. Кроме того, использование математических моделей позволяет значительно ускорить процесс анализа текстов.

Каким образом математические модели используются в современной лингвистике?

В современной лингвистике математические модели используются для решения широкого круга задач, от анализа структуры языка до разработки систем машинного перевода и анализа текстов в социальных сетях.

Какие недостатки существуют у математических моделей в лингвистике?

Одним из основных недостатков математических моделей в лингвистике является то, что они не всегда могут учитывать все аспекты языка, в том числе контекст и семантику слов. Кроме того, разработка и применение математических моделей требует высокой математической подготовки и опыта в области компьютерных наук.

Видео по теме: