Когда появилась математическая логика

Математическая логика возникла в XIX веке как самостоятельная наука, изучающая формальные методы рассуждения и вывода. В статье рассматривается история развития математической логики и ее важность для современной науки и технологий.

Математическая логика – это раздел математики, изучающий формальные системы и методы вывода в них. Она является основой для многих других разделов математики и науки об искусственном интеллекте. История развития математической логики начинается в древности, но значительное развитие она получила только в XIX и XX веках.

Первые вехи в истории математической логики были положены древнегреческими философами. В V веке до нашей эры Парменид предложил логический подход к изучению реальности и формальную систему для описания мира. Позднее Аристотель разработал логику суждений и законов рассуждения, которые стали основой формальной логики.

Следующий важный этап в развитии математической логики наступил в XIX веке. Математики начали использовать формальные методы для доказательства теорем и развития математических конструкций. Так, в 1854 году Джордж Буль представил свою алгебру логики, которая впоследствии стала основой для развития булевой алгебры и логических операций.

В XX веке математическая логика получила строгую формализацию и стала самостоятельной наукой. Были разработаны аксиоматические системы, формальные системы вывода и методы математического доказательства. Важным вкладом в развитие математической логики стало также открытие парадоксов, которые привели к разработке новых теорий и концепций.

Современная математическая логика охватывает широкий спектр проблем и методов. Она стала неотъемлемой частью современной науки и технологий, а также нашла применение в области искусственного интеллекта и компьютерных наук.

История развития математической логики

История развития математической логики начинается с античности. Греки и индийские математики уже в древние времена занимались изучением формальной логики. Однако, настоящее развитие математической логики началось только в XIX веке.

Одним из важнейших вех в истории математической логики стало создание аксиоматической системы математики. В 20-х годах XX века были разработаны аксиомы, на основе которых можно было построить всю математику. Это стало возможным благодаря трудам Бертрана Рассела и Альфреда Норта Уайтхеда, которые в своей книге «Принципы математики» предложили аксиоматическую систему для математики.

В середине XX века развитие математической логики получило новый импульс с разработкой теории множеств. Заслуга в этом принадлежит немецкому математику Георгу Кантору, который в 1874 году предложил новый подход к изучению понятия множества и разработал теорию бесконечности.

Другим важным этапом в развитии математической логики стало появление теории моделей и математической логики первого порядка. Теория моделей, разработанная в 30-х годах XX века, позволила формализовать понятие математической структуры и исследовать ее свойства. Математическая логика первого порядка, в свою очередь, расширила возможности формализации математических теорий и позволила проводить более сложные доказательства.

Современная математическая логика продолжает развиваться и находит применение в различных областях науки и техники. Она является неотъемлемой частью компьютерных наук, искусственного интеллекта и других областей, где требуется точное и формальное мышление.

ПериодОсновные события

Древнее время	Изучение формальной логики греками и индийскими математиками
XIX век	Начало развития математической логики
20-е годы XX века	Создание аксиоматической системы математики
Середина XX века	Развитие теории множеств
30-е годы XX века	Появление теории моделей и математической логики первого порядка

Видео по теме:

Появление исторического фундамента

История развития математической логики начинается со времен античности. Однако, первые шаги в направлении формализации логических законов и символов были сделаны только в XIX веке.

Появление исторического фундамента математической логики связано с работами Жоржа Буля, который в 1854 году опубликовал свою известную книгу «Математический анализ логики». В этой книге Буль создал алгебру логики, в которой были определены основные операции (конъюнкция, дизъюнкция и отрицание) и законы, регулирующие их использование.

Дальнейшее развитие математической логики происходило благодаря работам других выдающихся ученых, таких как Готтлоб Фреге, который в 1879 году опубликовал свою книгу «Основания арифметики», и Альфред Норт Уайтхед вместе с Бертраном Расселом, которые в начале XX века выпустили свою знаменитую «Принципы математики».

Основные этапы развития математической логики

Античность

Первые шаги в развитии математической логики были сделаны в Древней Греции. В этот период великие математики, такие как Платон и Аристотель, занимались формализацией логических законов и доказательством математических утверждений.

Средние века

В Средние века математическая логика практически не развивалась. Большинство ученых того времени склонялись к авторитету Аристотеля и не вносили существенных новшеств в область логики.

Новое время

С развитием науки в эпоху Просвещения возникли новые идеи и концепции, которые повлияли на развитие математической логики. Изобретение символической логики Г. Лейбницем и разработка математической логики И. Буля стали важными этапами в развитии этой науки.

20 век

В 20 веке математическая логика претерпела революцию благодаря работам таких ученых, как Г. Фреге, Б. Рассел и Л. Витгенштейн. Они разработали новые методы формализации логических законов и представления математических доказательств.

Современность

Современная математическая логика продолжает развиваться и находит применение в разных областях науки и технологий. Она играет важную роль в компьютерных науках, искусственном интеллекте и других математических дисциплинах.

Вопрос-ответ:

Какова история развития математической логики?

Математическая логика развивалась на протяжении длительного времени. Самые первые идеи были сформулированы еще в древней Греции, но настоящий прорыв произошел в XIX веке. Ученые, такие как Лейбниц, Больцано и Лобачевский, внесли значительный вклад в развитие математической логики. В XX веке эта дисциплина стала еще более развитой и приобрела большое значение в различных областях науки и техники.

Когда появилась математическая логика?

Математическая логика появилась еще в древние времена. В древней Греции, Аристотель разработал базовые правила логического мышления и сформулировал первые логические аксиомы. Однако, настоящий прорыв в развитии математической логики произошел в XIX веке с появлением формальных методов и символов, таких как символы логических связок и кванторов.

Какие этапы прошла математическая логика?

Математическая логика прошла несколько этапов развития. Вначале, в древние времена, были разработаны основные принципы логического мышления и созданы первые логические аксиомы. Затем, в XIX веке, эта дисциплина стала развиваться более систематически с появлением формальных методов и символов. В XX веке математическая логика стала еще более развитой и приобрела большое значение в различных областях науки и техники.

Кто сделал вклад в развитие математической логики?

Множество ученых сделали значительный вклад в развитие математической логики. Некоторые из них включают Готтфрида Лейбница, который разработал бинарную систему исчисления и создал первые механические устройства для вычислений, Бернхарда Больцано, который внес вклад в теорию множеств и формулирование математической логики, и Николая Лобачевского, который разработал геометрию без постулатов параллельности. В XX веке также были множество ученых, таких как Георг Кантор, Бертран Рассел и Алонзо Черч, которые внесли значительный вклад в развитие математической логики.

Когда появилась математическая логика?

Математическая логика как самостоятельная дисциплина начала развиваться в конце XIX века.

Какие этапы развития прошла математическая логика?

Математическая логика прошла несколько этапов развития: классическая логика, формализация математики, появление аксиоматического метода, развитие теории множеств и теории моделей.

Что такое математическая логика?

Математическая логика — это дисциплина, изучающая формальные методы рассуждений и выводов в математике. Она используется для формализации математических объектов и описания математических теорий.

Развитие символической логики

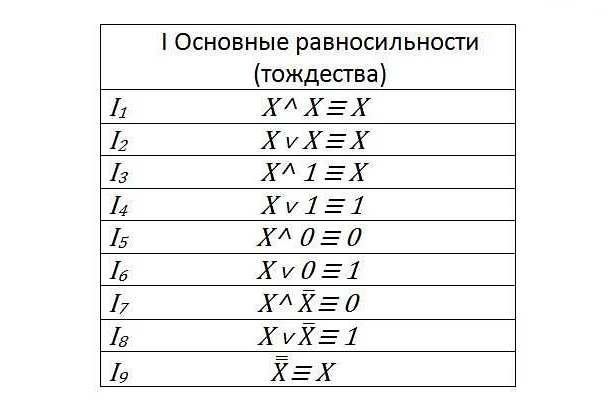
Первые шаги в развитии символической логики были сделаны в древней Греции. Философ Аристотель создал систему логики, основанную на категориях и силлогизмах. Однако, символическая логика, как наука, начала развиваться только в XIX веке.

Основоположником символической логики считается английский математик Джордж Буль. В 1854 году Буль ввел понятие булевых операций и символов для представления логических выражений. Он разработал алгебры логики и представил их в книге «An Investigation of the Laws of Thought» в 1854 году.

Следующий важный шаг в развитии символической логики был сделан Готтлобом Фреге в конце XIX века. Фреге разработал символическую систему логики первого порядка, основанную на идеях Буля. Эта система стала основой для дальнейшего развития математической логики.

В XX веке символическая логика стала развиваться все быстрее. Были созданы новые логические системы, такие как модальная логика, интуиционистская логика, моделирование вычислительных процессов с помощью логики и другие.

Символическая логика оказала огромное влияние на развитие математики, философии, информатики и других наук. Ее методы и инструменты используются для формализации и решения различных задач, а также для разработки компьютерных алгоритмов и искусственного интеллекта.

Роль математической логики в философии

Математическая логика играет важную роль в философии, поскольку она предоставляет строгий и формальный язык для выражения и анализа философских идей и аргументов. Философия и математическая логика взаимодействуют между собой, обогащая друг друга и способствуя развитию обоих дисциплин.

Математическая логика позволяет философам выражать свои идеи и аргументы в четкой и точной форме. Она предоставляет формальные методы для анализа и оценки рассуждений, позволяя выявить и устранить логические ошибки и противоречия. Благодаря математической логике философия становится более строгой и научной дисциплиной.

Вместе с тем, математическая логика также находит вдохновение в философии. Философские идеи и проблемы стимулируют развитие новых математических концепций и методов. Например, теория множеств и модальная логика развивались как результат философских исследований вопросов о множествах и необходимости.

Философия и математическая логика также обогащают друг друга своими методами и подходами. Философия предоставляет математической логике новые проблемы и вопросы для исследования, а математическая логика предоставляет философии формальные инструменты и методы анализа философских аргументов.

Таким образом, математическая логика и философия взаимодействуют и сотрудничают друг с другом, способствуя развитию и углублению обеих дисциплин. Они помогают философам формулировать и анализировать идеи, а также обеспечивают строгость и точность в их рассуждениях. Вместе они способствуют развитию науки и пониманию мира.

Влияние математической логики на компьютерные науки

Одним из основополагающих принципов математической логики является принцип двоичности, основанный на использовании двух значений — истины и лжи. Это позволяет компьютерам работать с бинарными данными и выполнять логические операции, такие как логическое И, логическое ИЛИ и логическое НЕ.

Также математическая логика используется в теории алгоритмов и структурах данных. Например, алгоритмический анализ основан на математической логике и позволяет определить сложность алгоритма и его эффективность. Структуры данных, такие как списки, деревья и графы, также обычно определяются с использованием математических моделей и логических операций.

Более того, математическая логика играет важную роль в области искусственного интеллекта. Логическое программирование и экспертные системы используют математическую логику для формулирования правил и вывода выводов на основе этих правил. Это позволяет компьютерам моделировать рассуждения и принимать решения, основанные на логических заключениях.

Таким образом, математическая логика играет ключевую роль в компьютерных науках, обеспечивая формальный и точный подход к решению задач различной сложности. Она помогает разработчикам создавать эффективные алгоритмы, программное обеспечение и системы искусственного интеллекта.

Логический парадокс и его влияние на развитие математической логики

Одним из наиболее известных логических парадоксов является парадокс Бертрана-Рассела, который был предложен в начале XX века. Этот парадокс возник в контексте теории множеств и привел к появлению важного раздела математической логики — теории типов.

Парадокс Бертрана-Рассела возникает при рассмотрении множества всех множеств, которые не содержат себя в качестве элемента. Вопрос состоит в том, должно ли это множество содержать само себя в качестве элемента или не должно. Если оно содержит само себя, то оно не должно содержаться, так как оно определено как множество всех множеств, не содержащих себя. Если же оно не содержит само себя, то оно должно содержаться, так как оно определено как множество всех множеств, не содержащих себя. Таким образом, возникает противоречие.

Парадокс Бертрана-Рассела побудил математиков и логиков искать новые подходы к формализации математической логики и развитию формальных систем, которые были бы лишены таких противоречий. В результате этого были созданы альтернативные логики, такие как интуиционистская логика и модальная логика.

Также парадокс Бертрана-Рассела стал важным фактором в развитии теории множеств и оснований математики. Постулирование аксиоматических систем и строгая формализация математических теорий стали одним из способов избежать логических парадоксов и обеспечить надежную основу для математического рассуждения.

Современное состояние математической логики

Современная математическая логика основана на аксиоматическом методе и формализации математических теорий. Она использует символы и правила вывода для описания и моделирования математических объектов и отношений. Логические системы, такие как исчисление высказываний и исчисление предикатов, являются основой для формализации математических теорий и доказательств.

Одной из важных областей развития математической логики является модельная теория. Она изучает структуры, которые удовлетворяют заданным алгебраическим и логическим условиям. Модельная теория позволяет анализировать свойства и отношения объектов внутри заданной теории, а также проводить исследования на предмет существования и уникальности моделей для различных теорий.

Современная математическая логика также активно используется в компьютерных науках. Она играет важную роль в разработке алгоритмов, программных языков и систем формальных доказательств. Логические системы, такие как исчисление высказываний и исчисление предикатов, предоставляют формальные основы для проверки корректности программ и алгоритмов.

Современная математическая логика продолжает активно развиваться и находить новые применения в различных областях. Она играет важную роль в развитии науки и технологий, позволяя более точно и строго описывать и анализировать математические объекты и рассуждения.

Перспективы развития математической логики в будущем

Одной из перспектив развития математической логики является ее применение в искусственном интеллекте. Математическая логика может быть использована для формализации и описания знаний, а также для разработки алгоритмов и моделей, используемых в искусственном интеллекте. Ее применение может существенно улучшить работу и эффективность искусственных интеллектуальных систем.

Важным направлением развития математической логики является разработка новых логических систем. Новые логические системы могут быть более мощными и гибкими, чем существующие, что позволит более точно описывать и анализировать различные явления и процессы. Такие системы могут быть применены в различных областях, включая философию, информатику, экономику и другие науки.

Другой перспективой развития математической логики является ее применение в криптографии и безопасности информации. Математическая логика может использоваться для разработки новых методов шифрования и аутентификации, а также для анализа и проверки безопасности различных систем и протоколов. Это позволит повысить уровень защиты информации и обеспечить безопасность в современном информационном обществе.

Также стоит отметить, что математическая логика будет продолжать влиять на развитие математики и других наук. Благодаря своей строгости и формальности, она является основой для доказательств и выводов в разных областях знания. Развитие математической логики будет способствовать развитию и совершенствованию других областей науки, а также созданию новых теорий и методов.

Таким образом, математическая логика имеет большое будущее и будет продолжать развиваться и применяться в различных областях. Ее перспективы развития включают применение в искусственном интеллекте, разработку новых логических систем, применение в криптографии и безопасности информации, а также влияние на развитие других наук. Развитие математической логики будет способствовать развитию науки и технологий в целом.