Кто придумал уравнения по математике

Узнайте, какие ученые и математики в истории придумали основные уравнения по математике и как они изменили наше понимание мира. Изучите вклад Арифметика, Геометрии и Алгебры в развитие математики.

Математические уравнения – это одно из основных понятий в математике. Они являются инструментом для описания и решения различных задач. Однако, их история насчитывает уже несколько тысячелетий.

В истории математики особое место занимают основатели алгебры и геометрии – двух важнейших разделов этой науки. Одним из первых математиков, который внес значительный вклад в развитие алгебры, был древнегреческий ученый Диофант Александрийский. Его работы посвящены решению алгебраических уравнений, а также исследованию свойств чисел и открытию новых методов решения задач. Диофант считается одним из основателей алгебры, благодаря своим работам, он внес существенный вклад в развитие математики в целом.

С другой стороны, геометрия развивалась в Древней Греции под руководством таких выдающихся ученых, как Пифагор, Евдокс и Евклид. Самым известным из них является, конечно же, Евклид, автор знаменитой «Элементов». В этом труде он изложил основные положения геометрии, включая теоремы, аксиомы и доказательства. Евклидова геометрия стала основой для различных научных открытий и применений в технике и архитектуре.

Таким образом, история математических уравнений неразрывно связана с вкладом выдающихся ученых в развитие алгебры и геометрии. Они создали основы этих наук, которые будут использоваться и развиваться вплоть до наших дней.

Древность: первые шаги в математике

Одной из самых важных древних цивилизаций, в которой зародилась математика, была Древняя Месопотамия. Математические знания в Месопотамии использовались для решения практических задач, таких как измерение земельных участков и торговые расчеты. Самым известным математическим трудом этой эпохи является «Шумерская математическая доска», на которой записывались числовые таблицы и решались уравнения.

Египетская цивилизация также внесла большой вклад в развитие математики. Египтяне использовали математику для строительства пирамид и решения задач, связанных с повседневной жизнью. Они разработали систему записи чисел, которая основывалась на десятичной системе счисления, и умели выполнять арифметические операции.

Древнегреческая математика считается основой современной алгебры и геометрии. Древние греки, в частности, Эвклид, Архимед и Пифагор, внесли огромный вклад в развитие математики. Эвклид написал знаменитую «Элементы», которая стала одной из самых влиятельных книг в истории математики. В ней он описал основы геометрии и алгебры, а также формализовал математическое доказательство.

Таким образом, математика имеет древнюю историю, начавшуюся еще задолго до нашей эры. Различные древние цивилизации и культуры внесли свой вклад в развитие алгебры и геометрии, создав основы современной математики, которые мы используем и изучаем до сих пор.

Древняя МесопотамияЕгипетская цивилизацияДревнегреческая математика

Зарождение математики

Использование в строительстве и повседневной жизни

Эвклид и «Элементы»

Видео по теме:

Египетские математики: знания и пирамиды

Одной из выдающихся особенностей египетской математики является их система записи чисел, называемая десятичной. В этой системе числа записывались с помощью символов, которые представляли различные степени числа 10. Например, символ для числа 1 был обозначен вертикальной чертой, символ для числа 10 — горизонтальной чертой и так далее. Эта система позволяла записывать и работать с числами любой величины, от 1 до нескольких миллионов.

Египетские математики также внесли значительный вклад в алгебру и геометрию. Они разработали методы решения различных алгебраических уравнений, таких как уравнения первой и второй степени. Они также использовали геометрические принципы для измерения земли и строительства пирамид. Например, они использовали знания о пропорциях и треугольниках для расчета размеров и углов пирамид.

Знания египетских математиков оказали большое влияние на другие древние цивилизации, такие как греки и римляне. Греки заимствовали и развили многие идеи египетской математики, включая систему записи чисел и основы геометрии. Римляне в свою очередь использовали знания египетских математиков для строительства своих инженерных сооружений.

В целом, египетские математики играли важную роль в развитии математики и архитектуры. Их достижения и знания оказали огромное влияние на последующие поколения математиков и инженеров, и их вклад в историю не может быть недооценен.

Математические открытия в античной Греции

Античная Греция считается родиной математики и ее развитие в этом регионе имеет особое значение для истории науки. Здесь были созданы основы алгебры и геометрии, которые впоследствии стали фундаментом для многих математических открытий и достижений.

Одним из самых известных математиков античной Греции был Пифагор. Он основал школу, которая стала известна как пифагорейская школа, и ввел понятие числа и его свойств. Пифагорейцы считали, что числа являются основой всего существующего и что они имеют гармонические отношения между собой. Это привело к открытию пропорций и отношений, которые стали основой для геометрии и алгебры.

Евклид, известный как «отец геометрии», также сделал значительный вклад в математические открытия. В его работе «Начала» он установил основные принципы геометрии, включая аксиомы и доказательства. Евклидова геометрия стала одной из основных ветвей математики и оказала огромное влияние на ее развитие вплоть до сегодняшнего дня.

Архимед, известный своими открытиями в области физики, также сделал важные открытия в математике. Он разработал методы интегрирования и изучал площади и объемы различных фигур. Его работа в области математики стала основой для развития интегрального исчисления и других математических концепций.

Таким образом, античная Греция была источником многих математических открытий, которые легли в основу алгебры и геометрии. Благодаря работе таких выдающихся ученых, как Пифагор, Евклид и Архимед, мы имеем современные математические концепции и инструменты, которые используем сегодня.

Алгебра и геометрия: труды Евклида

В «Началах» Евклид изложил основы геометрии, формализовал понятия прямой, угла, треугольника, окружности и других геометрических фигур. Он также разработал систему аксиом и логических доказательств, которые использовались в дальнейшем развитии математики.

Кроме геометрии, Евклид занимался и алгеброй. Он ввел понятие равенства и неравенства, работал с многочленами и рациональными числами. Его работы в алгебре были направлены на решение уравнений и разработку методов анализа чисел.

Труды Евклида оказали огромное влияние на развитие математики. Его систематический подход к геометрии и алгебре стал основой для многих последующих исследований и открытий. Евклидова геометрия применяется до сих пор и считается одной из основных областей математики.

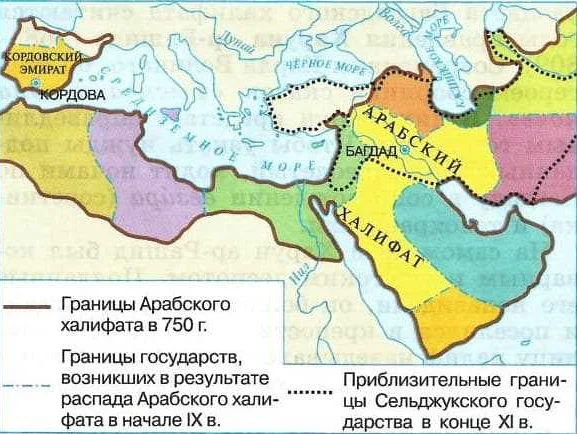
Арабский золотой век: развитие математики

Арабский золотой век, который пришелся на 8-13 века н.э., считается периодом высокого развития науки и культуры в арабском мире. В этот период многие арабские ученые активно занимались изучением и развитием математики.

Одним из наиболее известных математиков того времени был аль-Хорезми. Он сделал большой вклад в алгебру и геометрию, а его труды стали основой для последующих исследований и разработок.

Аль-Хорезми впервые ввел алгебраические символы и методы, которые мы используем и сегодня. Он разработал систему символов для представления неизвестных величин и операций над ними. Это позволило ему решать алгебраические уравнения и системы уравнений, а также разрабатывать новые методы решения математических задач.

В геометрии аль-Хорезми также внес значительный вклад. Он изучал свойства геометрических фигур и разработал методы их измерения и вычисления. С его помощью были созданы таблицы и справочники, содержащие значения тригонометрических функций, что существенно упростило выполнение геометрических расчетов.

Вместе с аль-Хорезми и другими математиками арабской эпохи, в этот период были также разработаны новые методы в области алгебры, геометрии и тригонометрии. Они внесли существенный вклад в развитие математики и стали основой для последующих исследований и открытий в этих областях.

Арабский золотой век с его развитием математики оказал огромное влияние на дальнейшее развитие науки и образования во всем мире. Он позволил совершить значительный скачок вперед в понимании и применении математических принципов и методов, которые мы используем и сегодня.

Ренессанс: открытия и переосмысления

Итальянский математик Леонардо Пизанский, известный как Фибоначчи, в своей книге «Liber Abaci» в 1202 году представил западной математике арабские числа и понятие нуля. Это открытие значительно упростило арифметические вычисления.

Во время Ренессанса также появились геометрические открытия. Итальянский математик Джероламо Кардано в своей книге «Ars Magna» (1545 год) ввел понятие мнимого числа и предложил решение кубических уравнений. Его работы сыграли важную роль в развитии алгебры.

Другим выдающимся математиком Ренессанса был Никколо Фонтана, известный как Тарталья. Он разработал метод решения кубических уравнений с положительными корнями. Тарталья опубликовал свои результаты в 1539 году, но изначально не раскрыл своего метода.

Эти открытия и переосмысления в математике Ренессанса подготовили почву для дальнейших разработок и привели к появлению новых теорий и понятий. Математика стала основой для многих других наук, играя важную роль в научном и интеллектуальном прогрессе.

МатематикГоды жизниВклад в развитие математики

Фибоначчи	1170-1250	Введение арабских чисел и нуля
Джероламо Кардано	1501-1576	Понятие мнимого числа и решение кубических уравнений
Никколо Фонтана (Тарталья)	1499-1557	Метод решения кубических уравнений с положительными корнями

Математические уравнения в новейшей истории

В новейшей истории математические уравнения продолжают играть важную роль в различных областях науки и технологий. С развитием компьютерных технологий и появлением новых методов решения уравнений, математики смогли решать более сложные и фундаментальные задачи.

Одной из самых значимых областей, где применяются математические уравнения, является криптография. Криптография — это наука о защите информации с помощью шифрования. Для создания безопасных систем шифрования используются различные математические алгоритмы, основанные на решении сложных уравнений.

Еще одной областью, где математические уравнения играют важную роль, является машинное обучение и искусственный интеллект. Для построения моделей и алгоритмов, способных обрабатывать и анализировать большие объемы данных, требуется решение математических уравнений и оптимизация функций.

Также математические уравнения используются в физике, экономике, биологии и других научных областях. Они позволяют описывать сложные явления и взаимодействия в природе, а также проводить численные расчеты и прогнозы.

Новые открытия и разработки в области математических уравнений продолжают вносить важный вклад в науку и технологии. Решение сложных уравнений становится все более доступным и эффективным благодаря развитию компьютерных систем и новым методам решения.

Будущее математических уравнений

В будущем математические уравнения будут продолжать играть важную роль в науке и технологиях. С развитием компьютерных систем и алгоритмов, математики смогут решать еще более сложные и фундаментальные задачи.

Одной из перспективных областей, где математические уравнения могут найти новые применения, является квантовая физика. Квантовая физика изучает поведение частиц на микроуровне и требует решения сложных уравнений для описания таких явлений, как квантовый туннелинг и взаимодействие частиц.

Также математические уравнения будут использоваться для разработки новых алгоритмов и моделей в искусственном интеллекте. Разработка более эффективных и точных алгоритмов требует решения сложных уравнений и оптимизацию функций.

В целом, математические уравнения продолжат оставаться одной из основных инструментов для понимания и описания сложных явлений в науке и технологиях. Развитие методов решения уравнений и новые открытия в математике будут способствовать развитию научных и технологических достижений в будущем.

Современность: математика в наши дни

Современные математические исследования направлены на поиск новых решений сложных проблем и разработку новых методов и алгоритмов. Математики работают над различными теориями и моделями, которые помогают понять сложные физические явления, прогнозировать экономические тенденции и анализировать большие объемы данных.

Современные математические уравнения становятся все более сложными и абстрактными, требуют новых методов и техник для их решения. Математики используют компьютерные программы и высокопроизводительные вычислительные системы для численных расчетов и моделирования.

Математика также играет важную роль в криптографии и безопасности информации. Разработка новых криптографических алгоритмов и методов защиты данных требует глубоких знаний в области алгебры и теории чисел.

Современные математические исследования также осуществляются в области компьютерного зрения, искусственного интеллекта, робототехники, машинного обучения и других смежных областях. Математические модели и алгоритмы используются для разработки новых технологий и создания инновационных продуктов.

Вывод: математика продолжает оставаться фундаментальной наукой и неотъемлемой частью нашей современной жизни. Она является ключевым инструментом для понимания мира и решения сложных проблем. Без математики мы не смогли бы достичь таких высот в науке, технологиях и развитии общества.

Вопрос-ответ:

Кто придумал основы алгебры и геометрии?

Основы алгебры и геометрии были придуманы множеством ученых и математиков на протяжении многих столетий. Однако, можно выделить нескольких важных ученых, которые сделали значительный вклад в развитие этих областей. К ним относятся Брахмагупта, Ал-Хорезми, Эвклид, Архимед, Декарт, Ньютон и Лейбниц.

Какие основы легли в основу алгебры и геометрии?

Основы алгебры и геометрии основываются на систематизации и формализации математического знания. В алгебре основой являются арифметические операции и алгебраические уравнения. В геометрии основой являются формулы и принципы, описывающие отношения между точками, линиями и фигурами в пространстве.

Когда были созданы основы алгебры и геометрии?

Основы алгебры и геометрии были созданы в разные исторические периоды. Геометрия была развита в Древней Греции около 3-4 веков до нашей эры, в основном благодаря работам Эвклида и Архимеда. Алгебра начала свое развитие в Древнем Египте и Древней Индии около 2-3 веков до нашей эры, а затем была дальше развита в арабском мире в 9-10 веках. С течением времени эти области математики продолжали развиваться и совершенствоваться.

Какие великие математики внесли вклад в развитие алгебры и геометрии?

Существует множество великих математиков, которые внесли вклад в развитие алгебры и геометрии. Некоторые из них: Эвклид, Архимед, Декарт, Ньютон, Лейбниц, Гаусс, Эйлер, Лобачевский, Галуа, Риман, Кантор и многие другие. Каждый из них внес свой особый вклад в развитие этих областей математики, открыл новые теоремы и методы исследования.

Кто создал основы алгебры и геометрии?

Основы алгебры и геометрии были созданы многими учеными и математиками на протяжении многих веков. Однако, важно упомянуть двух великих ученых, которые внесли значительный вклад в развитие этих областей математики. Это Ал-Хорезми и Евклид.

Кто такой Ал-Хорезми?

Ал-Хорезми был известным ученым и математиком, который жил в IX веке. Он родился в Персии и является одним из ранних разработчиков алгебры. Ал-Хорезми оставил огромное наследие в виде своих работ, включая книгу «Об аль-джабр и аль-мукабала», которая стала основой для развития алгебры в западной математике.

Кто такой Евклид и какие основы он создал?

Евклид был древнегреческим математиком, который жил около 300 года до нашей эры. Он является автором «Элементов», одного из наиболее известных и влиятельных математических трудов в истории. «Элементы» содержат сведения о геометрии и алгебре, включая определения, аксиомы и доказательства, которые стали основой для развития геометрии и алгебры вплоть до современности.