Кто придумал числа в математике

В статье рассмотрены разные точки зрения на происхождение чисел в математике и представлены исторические факты о том, кто и каким образом придумал их. Узнайте о вкладе различных культур и ученых в развитие числовых систем и понятий в математике.

Числа являются одним из основных понятий математики. Они позволяют нам представлять и измерять количество, порядок и многое другое. Однако, задумывались ли вы, как и когда появились числа?

История чисел начинается очень давно, задолго до появления письменности и записи истории. Самое раннее доказанное употребление чисел относится к примерно 30 000 годам до нашей эры. Охотники и собиратели использовали примитивные символы для обозначения количества животных, ягод и других ресурсов.

Однако, понятие чисел, как мы их знаем сегодня, развилось значительно позже. Древние цивилизации, такие как древние египтяне и сумерцы, разработали свои собственные системы для записи чисел. Например, египтяне использовали гиероглифы для обозначения чисел, а сумерцы использовали клинопись на глиняных табличках.

Важно отметить, что в этих древних системах чисел не было нуля. Это было открыто только в Индии в V веке нашей эры. Индийские математики разработали десятичную систему с нулем, которая стала широко распространена и использовалась во многих других культурах.

Знания о числах продолжали развиваться в течение веков. В средние века арабские ученые сделали значительный вклад в развитие математики, включая открытие алгебры и разработку десятичной системы с позиционным представлением чисел.

Сегодня мы имеем огромное количество знаний о числах и их свойствах. Они используются во многих областях науки, техники и экономики. Но все началось с простых символов и понятий, которые появились тысячи лет назад. История чисел продолжается, и, кто знает, какие открытия еще ждут нас в будущем.

Истоки и развитие математики

Первые математические знания формировались у древних цивилизаций, таких как Месопотамия, Древний Египет, Древний Китай, Древняя Индия и др. В этих культурах люди разрабатывали системы счета, начинали изучать геометрию, арифметику, алгебру и другие ветви математики.

Одной из первых важных достижений в математике было изобретение системы чисел. Древние люди поняли, что для удобства счета и записи результатов необходимо использовать специальные символы, которые были обозначением для количества. Так появились десятичная, двоичная, шестнадцатеричная системы счисления и др.

С течением времени математика стала все более сложной и разнообразной. Великие математики разных эпох вносили свой вклад в развитие этой науки. Они разрабатывали новые теории, формулировали законы, решали сложные задачи. Благодаря их работе мы получили множество математических понятий и методов, которые широко применяются в различных областях науки и техники.

Сегодня математика является основой для многих других наук. Она помогает нам понять и объяснить мир вокруг нас, решать задачи различной сложности, прогнозировать явления и разрабатывать новые технологии. Без математики невозможно представить современное общество и его достижения.

Таким образом, истоки математики уходят в глубокую древность, а ее развитие продолжается и по сей день. Математика – это неотъемлемая часть нашей жизни, которая помогает нам понять и описать мир вокруг нас.

Видео по теме:

Происхождение первых чисел

Древние цивилизации, такие как египтяне и шумеры, использовали специальные символы для обозначения чисел. Например, египтяне использовали изображения пальцев и птиц для обозначения единиц, десятков и сотен.

В Древней Греции появились первые математические системы. Пифагорейцы считали числа основой всего существующего и развивали математику как науку. Они ввели понятие натуральных чисел, которые включали 0 и все положительные числа.

С развитием торговли и обмена благами появилась необходимость в отрицательных числах. Однако их использование вызывало споры и смущение в течение многих веков.

В середине 7 века индийские математики предложили использовать символ 0 для обозначения нуля. Это стало революционным открытием, так как позволило более удобно выполнять арифметические операции и записывать числа.

В средние века, с развитием арабской математики, была введена десятичная система счисления, которую мы используем до сих пор. Она основана на позиционном принципе, где значение числа зависит от его положения в числе.

Таким образом, происхождение первых чисел связано с потребностями людей в счете и измерении, и с течением времени математика развивалась и становилась все более сложной и универсальной наукой.

Развитие идеи числа в Древнем Египте

Древний Египет считается одним из первых цивилизаций, где зародилась математика. Египтяне использовали числа для множества практических задач, таких как измерение земельных участков, подсчет имущества и др.

В Древнем Египте использовалась система счисления, основанная на десятичной системе. Египтяне использовали символы для обозначения чисел: вертикальные стрелки для единиц, горизонтальные стрелки для десятков, кружки для сотен и так далее. Они также использовали специальный символ «алый» для обозначения нуля.

Египтяне умели выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление. Они использовали специальные методы и алгоритмы для выполнения этих операций, такие как метод двоичного разложения числа для умножения и деления.

Одним из известных математических текстов, найденных в Древнем Египте, является папирус Ахмеса. В нем содержатся различные математические задачи, включая вычисление площади прямоугольника, объема пирамиды и др.

Развитие идеи числа в Древнем Египте имело большое значение для развития математики в целом. Египтяне не только использовали числа для практических задач, но и разработали различные методы и алгоритмы, которые стали основой для дальнейшего развития математики в других культурах.

Вопрос-ответ:

Какие числа считаются самыми древними в истории математики?

Самыми древними числами в истории математики считаются натуральные числа, то есть числа, которыми считаются единицы, двойки, тройки и так далее.

Кто и когда впервые придумал идею использовать числа для обозначения количества?

Идею использовать числа для обозначения количества придумали древние цивилизации, такие как Древний Египет и Древний Вавилон, около 3000 года до нашей эры.

Какие системы счисления существовали в древности и в каких странах они использовались?

В древности существовали различные системы счисления, включая египетскую, вавилонскую, греческую и римскую. Египетская система счисления использовалась в Древнем Египте, вавилонская — в Древнем Вавилоне, греческая — в Древней Греции, а римская — в Древнем Риме.

Когда были открыты отрицательные числа?

Отрицательные числа были открыты в Древней Индии в V веке нашей эры. Они были введены для решения математических проблем, связанных с долгами и учетом.

Кто изобрел ноль и какая роль у него в математике?

Ноль был изобретен в Индии в V веке нашей эры и стал одним из важнейших открытий в истории математики. Ноль позволяет обозначать пустоту и играет ключевую роль в различных математических операциях, таких как сложение, вычитание и умножение.

Индусская математика: от нумерации до десятичной системы

Первые упоминания о числах в индусской математике относятся к III-II векам до нашей эры. Индийские математики использовали специальные символы для обозначения чисел, которые сочетали в себе цифры и степени десяти. Эта система нумерации получила название «брахми» и считается одной из самых ранних в мировой истории.

Важным достижением индусской математики было введение понятия нуля. Индийские математики поняли, что такое отсутствие числа и разработали специальный символ для его обозначения. Это стало важной составляющей для дальнейшего развития математики и появления десятичной системы счисления.

Одним из известных индийских математиков является Арябхата. В VII веке он разработал свою систему нумерации, которая включала в себя десять символов и позиционное представление чисел. Эта система была базой для развития десятичной системы счисления, которая впоследствии стала стандартом во многих странах мира.

Индусская математика оказала значительное влияние на развитие математики во всем мире. Ее достижения в области нумерации и разработке десятичной системы счисления стали фундаментом для современной мировой математики и ее применения в науке и технологии.

Таким образом, индусская математика играет важную роль в истории появления чисел в математике. Ее разработки и достижения стали основой для развития современных систем счисления и вносят вклад в наше ежедневное использование чисел и математических операций.

Особенности развития чисел в Китае

Числа и математика имеют огромное значение в китайской культуре и истории, и их развитие в Китае имеет свои особенности. В Китае числа играли важную роль в различных аспектах жизни, включая астрологию, геометрию, календарь, медицину и другие области.

Одной из особенностей китайской системы чисел является использование позиционной нотации. В китайской позиционной системе каждая позиция числа имеет свое значение, и значение числа определяется суммой значений всех его позиций. Например, число 123 представляется как 100 + 20 + 3.

Китайские числа записываются с использованием китайских иероглифов, что отличает их от арабских или римских чисел. Китайские иероглифы для чисел имеют свою уникальную форму и часто имеют связь с их значениями. Например, иероглиф для числа «один» похож на вертикальную линию, а иероглиф для числа «два» имеет две горизонтальные линии.

Китайская система чисел также отличается от западной системы чисел тем, что не использует разделительные символы, такие как запятая или точка. Вместо этого, числа разделяются на группы по четыре цифры, начиная с младших разрядов. Например, число 123456789 будет записано как «12,3456,789».

Китайская цифраКитайская записьЗначение

零	ноль	0
一	один	1
二	два	2
三	три	3
四	четыре	4

Китайская система чисел также имеет свои собственные символы для больших чисел. Например, символ для миллиона представляет собой сочетание двух иероглифов, а символ для миллиарда состоит из трех иероглифов.

Китайские математики внесли значительный вклад в развитие чисел и математики в целом. Они разработали различные методы вычислений, включая методы счета на счетах и использование абака. Китайские математики также внесли вклад в развитие геометрии, алгебры и тригонометрии.

Сегодня китайские числа и их системы все еще используются в Китае и других странах, где китайский язык является официальным или используется в торговле и культуре. Их уникальные особенности и история делают их важной частью мировой математики и культуры.

Западная математика: алфавитные системы числения

Римская система числения основана на использовании латинского алфавита. В этой системе числа обозначаются специальными символами: I, V, X, L, C, D, M. Каждый символ имеет свою числовую ценность, и числа получаются путем сложения или вычитания этих символов. Например, число 6 записывается как VI (5 + 1), а число 9 — как IX (10 — 1).

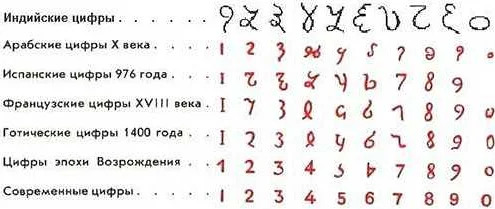
Еще одной алфавитной системой числения является арабская система, которая на сегодняшний день является наиболее распространенной. Арабские цифры, которые мы используем в повседневной жизни (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), также являются алфавитными символами. Эта система числения была разработана в Индии и впервые была введена в Европе в 10 веке.

Как и римская система, арабская система числения основана на позиционном принципе. В этой системе каждая цифра имеет свою числовую ценность в зависимости от своего положения в числе. Так, число 123 представляет собой сумму 100, 20 и 3.

Алфавитные системы числения играли и продолжают играть важную роль в математике и науке. Они позволяют нам записывать и работать с числами, делая математические вычисления более удобными и понятными. Каждая система имеет свои особенности и применения, и их изучение помогает нам лучше понять историю развития математики.

Появление нуля и отрицательных чисел

Появление нуля относится к различным культурам и периодам времени, история которых связана с разными практиками и системами счёта. Один из самых ранних примеров использования нуля – представление числа «ноль» на индийском континенте в III веке до н.э. Благодаря этому открытию стало возможным вводить позиционную систему счисления и производить сложение, вычитание и умножение чисел.

Отрицательные числа в истории математики появились позже. Их использование началось с появления задач и ситуаций, в которых требовалось измерять отрицательные значения. Примерами таких ситуаций могут быть задачи о движении объектов или оценке температуры. Понятие отрицательных чисел было введено в арабской математике в IX веке, а затем было перенято и развито в европейской математике в Средние века.

Появление нуля и отрицательных чисел было важным шагом в развитии математики, сделавшим возможным решение новых задач и расширение областей применения математических концепций.

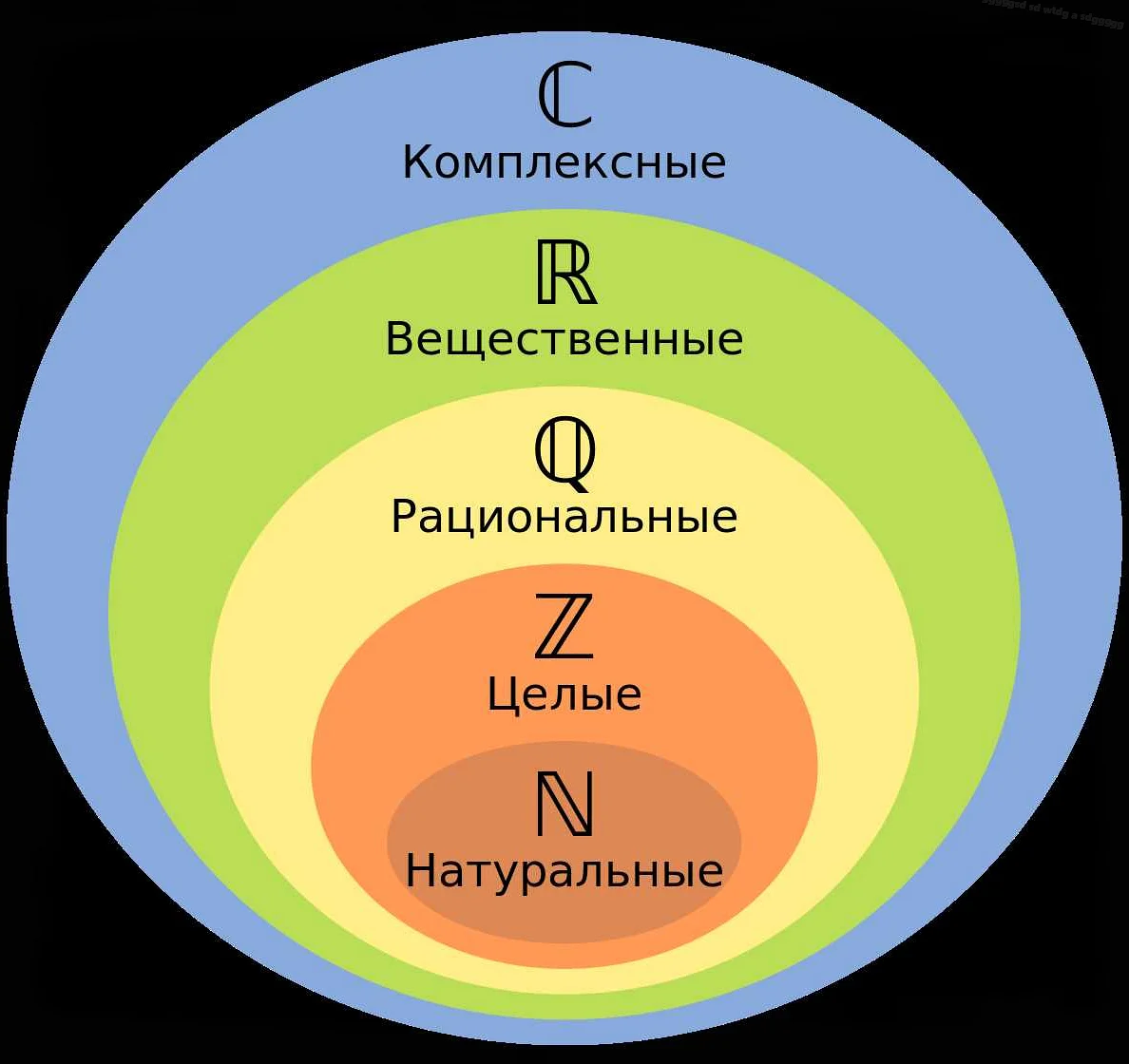
Современные математические системы чисел

В современной математике существует несколько различных систем чисел, которые используются для решения различных задач и проблем. Эти системы чисел отличаются друг от друга своими свойствами и применением.

Одной из наиболее распространенных систем чисел является система натуральных чисел, которая включает в себя все положительные числа, начиная с единицы. Натуральные числа используются для подсчета и измерения количества объектов или явлений.

Другой важной системой чисел является система целых чисел, которая включает в себя все натуральные числа, а также их отрицания и ноль. Целые числа используются для представления долгов, температур, расстояний и других величин, которые могут быть как положительными, так и отрицательными.

Система рациональных чисел включает в себя все числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа используются для точного представления долей и долей от целых чисел.

Система действительных чисел включает в себя все рациональные числа, а также иррациональные числа, которые не могут быть представлены в виде дроби. Действительные числа используются для представления точных величин, таких как длина, площадь и объем.

Наконец, существует система комплексных чисел, которая включает в себя вещественную и мнимую части. Комплексные числа используются в математической физике и электротехнике для моделирования и решения сложных задач и уравнений.