Как найти координаты точки на графике: полезные советы по математике

Узнайте, как найти координаты точки на плоскости или в пространстве с помощью геометрических формул и алгоритмов. Познакомьтесь с системами координат и узнайте, как использовать их для определения местоположения объектов в математике.

Нахождение координат точки на плоскости — одна из основных задач в математике. Это необходимое умение для решения многих задач, включая построение графиков функций, рассчет расстояния между точками, решение геометрических задач и многое другое.

В этой статье мы рассмотрим простые способы и формулы для нахождения координат точки на плоскости. Они понадобятся нам для решения различных задач и вычислений.

Мы также разберемся с тем, что такое система координат и как ее использовать для нахождения координат точки на плоскости. Кроме того, вы узнаете про другие методы нахождения координат, такие как использование формул для расстояния между точками и нахождения угла между двумя векторами.

Описание темы статьи

Наверняка каждый из нас сталкивался с необходимостью найти координаты точки на плоскости. Эта задача имеет широкое применение в геометрии, физике и многих других областях науки и техники. В этой статье мы рассмотрим несколько простых способов и формул для нахождения координат точки, заданной различными способами.

Начнем со стандартного способа – определения координат точки по ее расстоянию от начала координат. Для этого мы используем формулу расстояния между двумя точками в прямоугольной системе координат. Также мы рассмотрим способы нахождения координат точки, заданной углом и расстоянием от начала координат, а также координат точки, заданной расстоянием до двух других точек.

Важно понимать, что нахождение координат точки на плоскости – это не просто математическая задача, но и задача, требующая умения визуализировать объекты на плоскости и понимания взаимного расположения точек. Поэтому в этой статье мы также рассмотрим некоторые приемы и советы, которые помогут вам лучше представить себе грубое положение точки на плоскости и легче решать задачи, связанные с координатами точек.

Видео по теме:

Что такое координаты точки на плоскости?

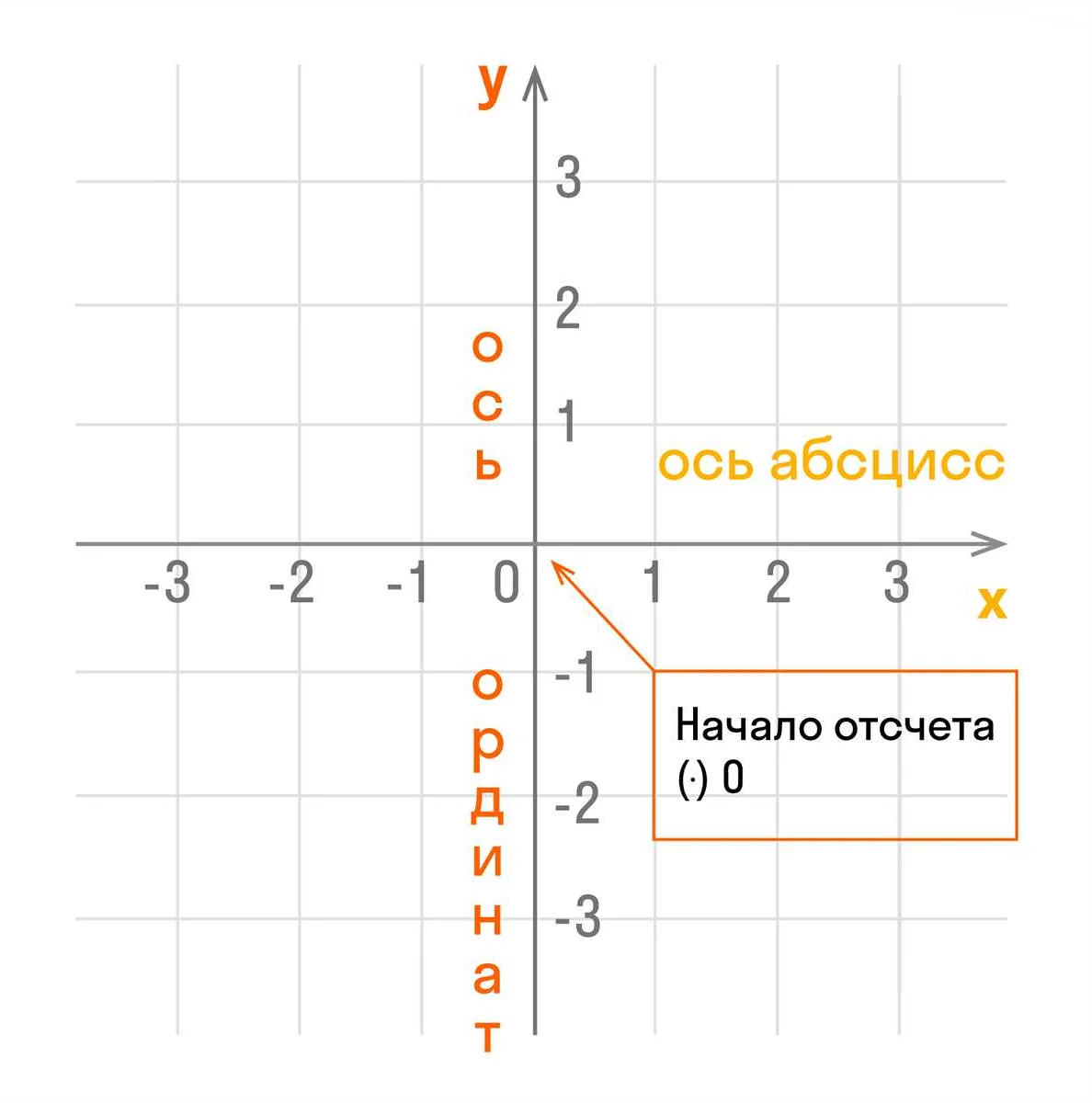
Координаты точки на плоскости – это числа, которые задают положение точки относительно начала координат, который считается точкой (0,0) и находится в центре плоскости. Первое число (x) обозначает расстояние от начала координат до точки по оси абсцисс (горизонтальная ось), а второе число (y) обозначает расстояние от начала координат до точки по оси ординат (вертикальная ось).

Координаты точки задаются в виде упорядоченной пары чисел (x,y), где x – это значение по оси OX, а y – по оси OY. Зачастую, для удобства, координаты точек на плоскости отмечаются на графике с помощью точек, линий и кратких вычислительных символов, таких как угловые скобки или круглые скобки.

В математике координаты точек на плоскости используются, например, для решения задач геометрии или для построения графиков функций. Понимание принципа нахождения координат точек на плоскости является необходимым для дальнейшего изучения геометрии и математики в целом.

Определение координат

Координаты точки на плоскости указывают ее положение относительно начала координат. Для определения координат точки на плоскости необходимо провести две оси: ось X и ось Y, которые пересекаются в начале координат. Ось X является горизонтальной, а ось Y вертикальной.

Чтобы определить координаты точки, необходимо провести перпендикуляры от точки на каждую ось. То, насколько далеко от начала координат расположена точка на оси X, указывает ее координату X. Аналогично, координата Y определяется по расстоянию точки от начала координат по оси Y. Измерение координат принято измерять в единицах измерения длины, таких как сантиметры, метры или пиксели.

Существует также альтернативный способ записи координат точки на плоскости — декартовы координаты. Они представляют собой упорядоченную пару чисел (x, y), где x — это координата по оси X, а y — по оси Y. Пример записи координат точки A: (2, 5).

Знание как найти координаты точки на плоскости является необходимым для решения многих задач в математике, физике, инженерии, программировании и других научных дисциплинах.

Оси координат

Оси координат — это система координат, используемая для определения положения точек на плоскости. Она состоит из двух перпендикулярных прямых: оси Х и оси Y. Точка пересечения осей называется началом координат. Она имеет координаты (0,0).

Ось Х расположена горизонтально и обозначает горизонтальные значения координат. Ось Y расположена вертикально и обозначает вертикальные значения координат. Каждая точка на плоскости может быть определена с помощью пары координат (x, y), где x — значение точки на оси Х, а y — значение точки на оси Y.

Координаты точки могут быть отрицательными или положительными в зависимости от того, на какой стороне начала координат точка расположена. Координаты точки (x,y) будут отрицательными, если она расположена слева или ниже начала координат.

Оси координат используются в геометрии, физике, экономике и других науках для определения расстояний и направлений, а также для построения графиков функций и решения уравнений.

Для удобства визуализации на плоскости обычно нарисованы рядом с осями координат стрелки, указывающие направления осей, а также нарисованы сетки, размеченные по шкалам значений на оси X и Y.

Важно помнить: Оси координат образуют правую систему координат, что означает, что ось X направлена вправо, а ось Y — вверх. При работе с осами координат следует быть внимательным при определении координат точек на плоскости.

Как найти координаты точки на плоскости с помощью графика?

Чтобы найти координаты точки на плоскости с помощью графика, нужно составить уравнение прямой, на которой лежит данная точка. Для этого нужно знать хотя бы две точки на прямой, через которые можно провести эту прямую.

Затем, используя координаты этих двух точек, можно найти угловой коэффициент прямой (k) и значение ее свободного члена (b) по формуле k = (y2 — y1)/(x2 — x1) и b = y1 — kx1.

Подставив координаты искомой точки в уравнение прямой (y = kx + b), можно найти ее координаты на плоскости.

Если же даны только координаты точки, без информации о прямой, на которой она лежит, можно использовать график для определения примерного месторасположения точки и приблизительно подобрать координаты.

Например, если точка находится в правом верхнем углу квадрата на графике, где каждая сторона квадрата равна 1, то ее координаты будут примерно равны (1,1).

В любом случае, знание основ математики и умение работать с графиками помогут найти координаты точки на плоскости.

Описание метода

Для того чтобы найти координаты точки на плоскости, необходимо знать её расположение относительно координатных осей. Координатные оси X и Y пересекаются в центре координат, который имеет координаты (0, 0).

Чтобы определить координаты точки, необходимо измерить расстояние от точки до оси X (абсцисса) и расстояние от точки до оси Y (ордината). Эти расстояния можно выразить в единицах измерения координатной сетки.

Если точка находится над осью X, то её ордината будет положительной, если же точка находится под осью X, то ордината будет отрицательной. Аналогично, если точка находится правее оси Y, то её абсцисса будет положительной, а если точка находится левее оси Y, то абсцисса будет отрицательной.

Измерив расстояния до осей и определив знаки координат, можно записать координаты точки в виде упорядоченной пары чисел (x, y), где x обозначает абсциссу, а y обозначает ординату.

Например, если точка находится 3 единицы справа от оси Y и 2 единицы выше оси X, то её координаты будут (3, 2).

Примеры

Рассмотрим несколько примеров вычисления координат точек на плоскости в математике:

• Пример 1. Дана точка A с координатами (2, 3) и вектор V(4, 5). Найдем координаты точки B, находящейся на расстоянии 3 от точки A в направлении вектора V. Для этого используем формулу B = A + kv, где k – параметр, равный длине вектора AV, деленной на длину вектора V, то есть k = |AV| / |V|. В данном случае получаем: k = |AV| / |V| = (sqrt((3-5)^2 + (2-4)^2)) / (sqrt(4^2 + 5^2)) = 1.076. Тогда координаты точки B будут: B = A + kv = (2, 3) + 1.076(4, 5) = (6.44, 8.38).
• Пример 2. Даны точки A(2, 3), B(5, 6) и C(7, 1). Найдем координаты точки D, которая делит отрезок AC в отношении 2:3. Для этого нужно использовать формулу D = (3C + 2A) / 5. Подставляем координаты точек: D = (3(7, 1) + 2(2, 3)) / 5 = (23/5, 1/5).
• Пример 3. Дана точка A(2, 3) и прямая l, проходящая через точки B(4, 1) и C(1, 4). Найдем координаты точки D, являющейся проекцией точки A на прямую l. Для этого нужно найти уравнение прямой l и затем использовать формулу проекции точки на прямую, D = ((Ax+By+C)/(A^2+B^2)) * (A,B) – (C/(A^2+B^2)) * (B,A), где (A,B) и (B,A) – направляющие векторы прямой l. Найдем уравнение прямой, используя координаты точек B и C: B — C = (3, -3), значит, (A,B) = (3, -3) и (B,A) = (-3, 3). Тогда: D = ((2*3+3*(-3)+(-9))/(3^2+(-3)^2)) * (3,-3) – ((-9)/(3^2+(-3)^2)) * (-3,3) = (5/2, 1/2).

Как найти координаты точки на плоскости с помощью расстояния до осей координат?

Чтобы найти координаты точки на плоскости с помощью расстояния до осей координат, необходимо знать расстояния от точки до осей координат. Зная расстояние от точки до оси X и расстояние от точки до оси Y, можно легко определить координаты точки.

Например, пусть нам дана точка А, расстояние от которой до оси X равно а, а расстояние до оси Y равно b. Тогда координаты точки А будут равны (а, b).

Чтобы вычислить расстояния от точки до осей координат, можно воспользоваться теоремой Пифагора. Для расстояния от точки до оси X нужно найти катет, равный расстоянию от точки до оси Y, и гипотенузу, которая будет равна расстоянию от начала координат до точки. Аналогично вычисляется расстояние от точки до оси Y.

Таким образом, чтобы найти координаты точки на плоскости с помощью расстояния до осей координат, нужно знать расстояния от точки до осей X и Y, и затем подставить их в соответствующие координаты.

Описание метода

Найти координаты точки на плоскости можно с помощью двух способов: координатной и векторной. Оба способа являются простыми и эффективными.

Координатный способ

Координатный способ заключается в определении координат точки по ее расстоянию от осей координат. Для этого требуется знать расстояние точки по горизонтальной оси (ось абсцисс) и по вертикальной оси (ось ординат). Затем координаты точки выражаются в виде (x,y), где x – расстояние от точки до оси абсцисс, y – расстояние от точки до оси ординат.

Векторный способ

Векторный способ заключается в определении координаты точки на основе ее положения относительно начала координат и вектора, соединяющего начало координат с этой точкой. Вектор задается двумя координатами: x и y. При помощи формулы для вычисления координат точки на основе вектора, можно быстро вычислить координаты точки на плоскости.

• Координатный способ – подходит для нахождения координат точек, для которых известны расстояния до осей координат.
• Векторный способ – подходит для нахождения координат точек на основе вектора, соединяющего начало координат с этой точкой.

В обоих методах для определения координат точки требуются начальные условия и формулы, по которым происходит вычисление координаты точки.

Примеры

Пример 1:

Найти координаты точки М, если известно, что она делит отрезок AB в отношении 2:3, где А (-2, 4), а B (4, -6).

Решение:

Для нахождения координат точки М используем формулу:

xM = (xB — xA) * k + xA

yM = (yB — yA) * k + yA

Где k = AM / AB = 2 / 5.

Подставляем известные значения:

xM = (4 — (-2)) * 2/5 + (-2) = -0.4

yM = (-6 — 4) * 2/5 + 4 = 1.2

Итак, координаты точки M равны (-0.4, 1.2).

Пример 2:

Найти координаты точки пересечения прямых y = 2x + 3 и y = -x + 5.

Решение:

Для нахождения координат точки пересечения прямых подставим уравнения прямых в систему уравнений и решим ее:

xy

y = 2x + 3	1	5
y = -x + 5	4	1

Ответ: координаты точки пересечения прямых равны (1, 5).

Пример 3:

Найти расстояние между точками A(-3, 5) и B(2, -2).

Решение:

Для нахождения расстояния между точками используем формулу:

d = sqrt((xB — xA)2 + (yB — yA)2)

Подставляем известные значения:

d = sqrt((2 — (-3))2 + (-2 — 5)2) = sqrt(74).

Итак, расстояние между точками A и B равно sqrt(74) единиц.

Как найти координаты середины отрезка на плоскости?

Координаты середины отрезка — это точка, которая делит отрезок пополам. Найдем ее координаты.

Для начала, нам нужно знать координаты концов отрезка. Пусть точки A и B имеют координаты (x1, y1) и (x2, y2) соответственно.

Чтобы найти координаты середины отрезка AB, нужно:

1. Найти среднее значение x-координат точек A и B: (x1 + x2) / 2 = x.
2. Найти среднее значение y-координат точек A и B: (y1 + y2) / 2 = y.

Таким образом, координаты середины отрезка AB будут (x, y).

Пример:

Точка AТочка BСередина AB

(2, 4)	(6, 10)	(4, 7)
(-3, 1)	(5, -7)	(1, -3)

Итак, для того чтобы найти координаты середины отрезка на плоскости, нужно просто найти среднее значение x- и y-координат концов отрезка.

Формула для нахождения координат середины отрезка

Координаты середины отрезка на плоскости могут быть найдены с помощью формулы

M = ((x1 + x2) / 2, (y1 + y2) / 2)

где (x1, y1) и (x2, y2) — координаты концов отрезка.

Эта формула основывается на том, что координаты середины отрезка — это среднее значение координат концов отрезка.

Например, для отрезка AB с конечными точками A(2, 8) и B(10, 4) координаты середины отрезка можно вычислить следующим образом:

• Координаты x: ((2 + 10) / 2) = 6
• Координаты y: ((8 + 4) / 2) = 6

Следовательно, координаты середины отрезка AB: M(6, 6).

Эта формула является простой и может быть использована для нахождения координат середины отрезка на плоскости в любых задачах, где это необходимо.

Примеры

Рассмотрим пример нахождения координат точки на плоскости. Пусть дана точка А с координатами (3; 5) и мы хотим найти координаты точки В, находящейся на расстоянии 8 единиц от точки А.

1. Решение геометрическим путем: Найдем окружность с центром в точке А и радиусом 8 единиц. На этой окружности находятся две точки — точки В и С. Используя свойства геометрической фигуры, получаем, что точка В имеет координаты: (3+4; 5+sqrt(48)) или (3+4; 5-sqrt(48)), в зависимости от того, по которую сторону от оси Ох находится точка В.

2. Решение алгебраическим путем: Используем формулы нахождения расстояния между двумя точками на плоскости и формулы нахождения координат точки, лежащей на заданном расстоянии от заданной точки.

Расстояние между точками А и В равно 8 единиц. Значит, согласно формуле расстояния между точками на плоскости: (x2 — x1)^2 + (y2 — y1)^2 = 64, где x1 = 3, y1 = 5.Получаем уравнение окружности: (x-3)^2 + (y-5)^2 = 64. Чтобы найти координаты точки В, воспользуемся формулами нахождения координат точки, отстоящей от заданной точки на заданное расстояние:

• x = x1 + r*cos(α)
• y = y1 + r*sin(α)

где r=8, α — угол между осью Ох и отрезком, соединяющим точки А и В.

Рассмотрим три случая расположения точки В на плоскости и найдем соответствующие алгоритмы:

1. Если точка В находится на оси Ох, то α=0 или α=180 градусов. В этом случае получаем, что точка В имеет координаты (x1 ±r; y1).

2. Если точка В находится на оси Оу, то α=90 или α=270 градусов. В этом случае получаем, что точка В имеет координаты (x1 ; y1 ±r).

3. Если точка В расположена в любой другой точке, то необходимо найти угол α, используя теорему косинусов или синусов. Затем, подставив α в формулы нахождения координат точки, получаем координаты точки В.

Как найти расстояние между точками на плоскости?

В математике расстояние между двумя точками на плоскости можно определить с помощью формулы расстояния между двумя точками. Для этого нужно знать координаты этих точек.

Формула расстояния между двумя точками на плоскости:

d = √((x2 — x1)^2 + (y2 — y1)^2)

где d — расстояние между точками, x1 и y1 — координаты первой точки, x2 и y2 — координаты второй точки на плоскости.

Рассмотрим пример:

Точкаxy

А	3	4
В	7	1

Найдем расстояние между точками А и В:

d = √((7 — 3)^2 + (1 — 4)^2) = √(16 + 9) = √25 = 5

Ответ: расстояние между точками А и В равно 5 единицам.

Зная координаты двух точек, можно также использовать геометрический метод, измерив расстояние от одной точки до другой с помощью линейки или масштабированной сетки. Однако формула расстояния между точками на плоскости более точная и кроме того, позволяет найти расстояние между точками, не находящимися на одной прямой.

Формула для нахождения расстояния

В математике расстояние между двумя точками на плоскости можно найти, применяя формулу:

d = √((x2 — x1)² + (y2 — y1)²)

где d — расстояние между точками, x1 и y1 — координаты первой точки, x2 и y2 — координаты второй точки.

Расстояние между точками можно также вычислить, применяя теорему Пифагора для прямоугольного треугольника, образованного точками и началом координат:

d = √(x² + y²)

где d — расстояние между точками, x и y — координаты точки.

Эти формулы могут быть использованы в различных областях, таких как геометрия, физика, геодезия и т.д.

Примеры

Пример 1: Найти координаты точки C, если известны координаты точек A(2;4) и B(8;1), и отрезок AB делится точкой C в отношении 2:3.

Решение:

Сначала находим координаты точки C.

Для этого мы можем использовать формулу:

xC = xA + (xB — xA) × k

yC = yA + (yB — yA) × k

где k – коэффициент, определяющий соотношение расстояний AC и BC к отрезку AB, которое равно 2:3, то есть k = 2/(2+3) = 0,4.

Подставляем значения координат точек и находим:

xC = 2 + (8 — 2) × 0,4 = 4,4

yC = 4 + (1 — 4) × 0,4 = 2,6

Таким образом, координаты точки C равны (4,4;2,6).

Пример 2: Найти координаты точки D, которая равноудалена от точек A(3;1) и B(9;-3).

Решение:

Расстояние между точками A и D равно расстоянию между точками B и D. То есть:

AD = BD

Используем формулу расстояния между двумя точками в декартовой системе координат:

d(A,B) = √((xB — xA)² + (yB — yA)²)

Подставляем значения координат точек и получаем:

√((9 — 3)² + (-3 — 1)²) = √(6² + (-4)²) = √(36 + 16) = √52 ≈ 7,21

Таким образом, расстояние между точками A и B равно ≈7,21. Нам нужно найти точку D, которая находится на эквидистанте от точек A и B. Так как расстояние между двумя точками равно √(x2 — x1)² + (y2 — y1)², то находясь на равном расстоянии от точек A и B, мы будем находиться на середине отрезка AB. Следовательно, координаты точки D будут равны:

xD = (xA + xB)/2 = (3 + 9)/2 = 6

yD = (yA + yB)/2 = (1 — 3)/2 = -1

Таким образом, координаты точки D равны (6;-1).

Как найти координаты точки на плоскости, зная угол и расстояние до начала координат?

Найти координаты точки на плоскости можно разными способами в зависимости от имеющихся данных. Один из способов — найти координаты точки, зная угол и расстояние до начала координат.

Для этого необходимо использовать тригонометрические функции. Пусть угол между осью x и лучом, исходящим из начала координат и проходящим через точку, равен alpha, а расстояние до начала координат равно r.

Тогда координата x точки равна r*cos(alpha), а координата y — r*sin(alpha).

Приведенные формулы можно использовать для нахождения координат точки, если известны угол и расстояние до начала координат. Этот способ нахождения координат точки может быть полезен при решении задач, требующих нахождения координат точек на плоскости.

Описание метода

Для нахождения координат точки на плоскости необходимо знать ее расположение относительно осей координат. Ось OX горизонтальная и является основанием абсциссы, а ось OY вертикальная и является основанием ординаты.

Если известны расстояния точки до осей координат, то ее координаты можно вычислить с помощью простых формул. Например, если известны расстояния d1 и d2 от точки до осей OX и OY соответственно, то ее координаты (x, y) будут:

x =	d1 * cos(α)
y =	d2 * sin(α)

где α — угол, образованный отрезком, соединяющим точку с началом координат, и положительным направлением оси OX. Угол α можно вычислить, используя теорему Пифагора:

α = arctg(d2/d1)

Используя эти формулы, можно легко определить координаты точки на плоскости, зная ее расстояния до осей координат.

Примеры

Рассмотрим простейший пример нахождения координат точки на плоскости. Допустим, дана точка А с координатами (3;5). Найдём её координаты на 1 единицу выше по оси y. Для этого нужно прибавить к y-координате 1: (3;5+1)=(3;6).

Рассмотрим другой пример. Предположим, что у нас есть точка B со следующими координатами: (2;4). Найдём её координаты на 3 единицы ниже и на 2 единицы вправо. Для этого нужно вычитать 3 из y-координаты и прибавить 2 к x-координате: (2+2;4-3)=(4;1).

Еще один пример использования формулы – нахождение расстояния между двумя точками. Допустим, имеются точки C(1;-2) и D(-4;3). Найдем расстояние между ними. Сначала найдем разницу между соответствующими координатами: Δx=xD-xC=-4-1=-5 и Δy=yD-yC=3-(-2)=5. Затем применим формулу:

√[(-5)2+(5)2]=√(50)≈7.07. Таким образом, расстояние между точками С и D ≈ 7.07 единиц на плоскости.

Как найти координаты пересечения прямых на плоскости?

В математике пересечение прямых на плоскости представляет собой точку, где две прямые пересекаются. Найдем координаты этой точки.

Для начала нужно записать уравнения прямых в общем виде: y = kx + b1 и y = mx + b2, где k и m — угловые коэффициенты, b1 и b2 — значения функций в точке пересечения с осью y.

Далее приравняем уравнения: kx + b1 = mx + b2 и выразим x: x = (b2 — b1) / (k — m).

Теперь найдем значение y, подставив полученное значение x в одно из уравнений прямых: y = kx + b1 или y = mx + b2.

Таким образом, координаты точки пересечения прямых на плоскости будут иметь вид: (x, y).

Если прямые параллельны, то угловые коэффициенты будут равными, и формула для нахождения точки пересечения не будет работать. В этом случае необходимо использовать другие методы.

Как видно, формула для нахождения координат точки пересечения прямых на плоскости довольно проста и может быть использована при решении многих задач, связанных с геометрией и аналитической геометрией.

Описание метода

Координаты точки на плоскости определяются с помощью двух чисел, называемых координатами x и y. Координата x отображает позицию точки на горизонтальной оси, а координата y — на вертикальной оси. Для нахождения координат точки можно использовать несколько простых математических формул.

Метод 1: Графический способ

Для использования этого метода необходимо провести оси x и y на плоскости и отметить начало координат (0, 0). Затем одна координата измеряется вдоль оси x, а другая координата — вдоль оси y, от начала координат до точки, которую необходимо определить. Координаты точки получаются в результате пересечения двух линий, которые соответствуют измерениям по осям x и y.

Метод 2: Использование формулы

Для определения координаты x точки A на плоскости необходимо найти расстояние от точки A до вертикальной оси y (отметить это расстояние как d). Затем найти расстояние от начала координат до точки A по оси x (отметить это расстояние как a). Координата x будет равна a, а координата y определяется с помощью формулы y = +/- sqrt(r^2 — d^2), где r — расстояние от начала координат до точки A.

Если точка A находится на оси y, то координата x будет равна нулю, а координата y будет равна расстоянию от точки A до начала координат.

Таким образом, для определения координат точки на плоскости можно использовать графический способ или формулы. Оба метода являются простыми и могут быть использованы для решения задач разной сложности.

Примеры

Допустим, нам даны координаты точки A (5, 3) и мы хотим найти координаты точки В на 3 единицы выше и 2 единицы левее точки A. Для этого нам нужно вычесть из координат точки A соответствующие значения: x=5-2=3 и y=3+3=6. Получаем координаты точки B (3, 6).

Рассмотрим пример с нахождением расстояния между точками A(4, 7) и B(-2, 3). Используя формулу расстояния между двумя точками на плоскости, получаем: d = sqrt( (x2-x1)^2 + (y2-y1)^2 ) = sqrt( ( (-2) — 4 )^2 + (3-7)^2 ) = sqrt( 36 + 16 ) = sqrt(52) ≈ 7.21. Таким образом, расстояние между точками А и В ≈ 7.21 единиц.

Давайте рассмотрим пример поиска угла между осью x и отрезком, соединяющим начало координат и точку P (4, 8). Для этого мы используем формулу: угол = atan(y/x) = atan(8/4) ≈ 1.11 радиан или около 63.43 градусов.

Рассмотрим пример нахождения координат середины отрезка между точками P(2, 3) и Q(8, 12). Для этого нам нужно найти среднее арифметическое координат x и y каждой точки: x = (2 + 8)/2 = 5; y = (3 + 12)/2 = 7.5. Получаем координаты середины отрезка M(5, 7.5).

Как найти координаты точки на плоскости, зная уравнение прямой и расстояние до нее?

Чтобы найти координаты точки на плоскости, зная уравнение прямой и расстояние до нее, необходимо выполнить несколько простых действий. Во-первых, необходимо определить направляющий вектор прямой, для этого нужно записать уравнение прямой в общем виде.

Далее необходимо найти ортогональный вектор, проходящий через искомую точку на прямой. Для этого можно воспользоваться формулой нахождения расстояния от точки до прямой, которая выражается через модуль векторного произведения направляющего вектора прямой и вектора, соединяющего искомую точку с любой точкой на прямой.

Зная ортогональный вектор и направляющий вектор прямой, можно записать координаты искомой точки через параметрическое уравнение прямой. Например, если параметр t отвечает за движение по направляющему вектору прямой, то координаты точки на прямой можно найти по формулам:

x = x1 + t * kx

y = y1 + t * ky

где x1 и y1 — координаты любой точки на прямой, kx и ky — соответствующие координаты направляющего вектора, а t — параметр движения.

Однако, если параметрическое уравнение прямой неизвестно, можно воспользоваться системой уравнений, в которую входят уравнение прямой и уравнение окружности с центром в искомой точке и радиусом, равным расстоянию от точки до прямой.

Решить эту систему можно, например, методом подстановки или исключения переменных, подставляя выражение для одной из неизвестных в другое уравнение и получая квадратное уравнение относительно параметра t.

Таким образом, зная уравнение прямой и расстояние до нее, можно без труда найти координаты искомой точки на плоскости.

Описание метода

Существует несколько способов нахождения координат точки на плоскости, которые основываются на знании формул геометрии и алгебры. Один из таких методов — нахождение координат точки по ее расстоянию от начала координат и углу между этой точкой и положительным направлением оси x.

Для вычисления координат точки, необходимо знать ее расстояние r от начала координат и угол θ, который она образует с положительным направлением оси x. С помощью тригонометрических функций можно вычислить значения координат x и y точки:

• x = r * cos(θ)
• y = r * sin(θ)

Если известны координаты двух точек на плоскости (x1, y1) и (x2, y2), то можно вычислить координаты третьей точки с помощью формулы середины отрезка. Данный метод заключается в нахождении среднего значения координат x и y двух известных точек:

• x3 = (x1 + x2) / 2
• y3 = (y1 + y2) / 2

Также для вычисления координат точки можно использовать уравнение прямой, проходящей через известные точки на плоскости. Уравнение прямой можно записать в виде:

y = kx + b

где k — угловой коэффициент прямой, а b — свободный член. Вычислив значение углового коэффициента и свободного члена, можно определить координаты искомой точки, приравняв x и y к соответствующим выражениям:

• x = (y — b) / k
• y = kx + b

Примеры

Допустим, у нас есть точка P(3, 5) и мы хотим найти её координату по оси абсцисс, то есть значение x. В этом случае мы просто смотрим на первое число в скобках и видим, что координата x равна 3.

Если мы хотим найти координату точки Q, которая лежит на прямой AB, где A(1, 2) и B(4, 7), то мы можем воспользоваться формулой для нахождения уравнения прямой: y = kx + b. Находим k = (yB — yA) / (xB — xA) = (7 — 2) / (4 — 1) = 5/3. Затем находим b, подставляя известные значения: yA = 2, xA = 1, k = 5/3 — b. Получаем b = -1/3. Теперь мы можем подставить координаты точки Q(x, y) и решить систему уравнений: y = 5/3x — 1/3 и y = x + 1. Получаем x = 2 и y = 3.

Мы также можем использовать теорему Пифагора, чтобы найти расстояние между точками. Например, мы хотим найти расстояние между точками A(1, 2) и B(4, 7). Сначала находим длину отрезка AB по оси абсцисс: ABx = xB — xA = 4 — 1 = 3. Затем находим длину отрезка AB по оси ординат: ABy = yB — yA = 7 — 2 = 5. Теперь мы можем применить теорему Пифагора: AB = √(ABx² + ABy²) = √(3² + 5²) = √34.

• Точка M лежит на прямой AB, где A(1, 2) и B(4, 7). Координаты точки M можно найти, зная, что AM = BM / 3. Найдём BM: BM = √((xB — xA)² + (yB — yA)²) = √(3² + 5²) = √34. Тогда AM = BM / 3 = (√34) / 3. Найдём координаты точки M: xM = (xA + 2xB) / 3 = (1 + 8) / 3 = 3, yM = (yA + 2yB) / 3 = (2 + 14) / 3 = 16 / 3.
• Для нахождения точки пересечения прямых AB и CD, где A(2, 3), B(5, 8), C(1, 6) и D(6, 1), нужно решить систему уравнений:
  • y = k1x + b1, где k1 = (yB — yA) / (xB — xA) = 5/3, b1 = yA — k1xA = -1/3.
  • y = k2x + b2, где k2 = (yD — yC) / (xD — xC) = -5/5 = -1, b2 = yC — k2xC = 11.
• Решение системы уравнений дает x = 1.6 и y = 3.2, то есть точку пересечения прямых находится в точке P(1.6, 3.2).

Как найти угол между векторами на плоскости?

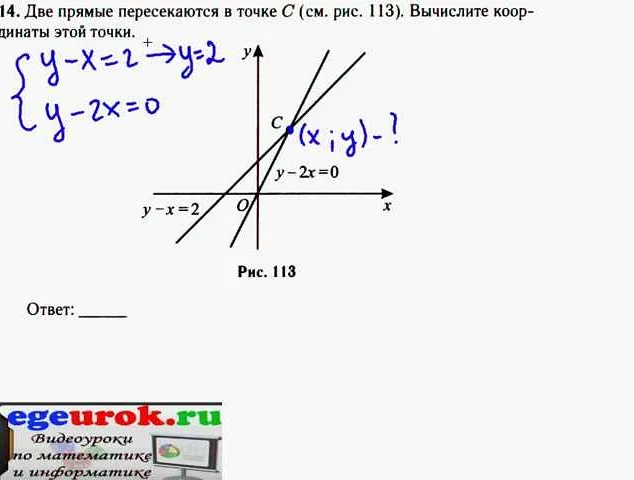
Найти угол между двумя векторами на плоскости можно с помощью формулы скалярного произведения векторов:

cos(α) = (a · b) / (|a|*|b|)

где α — искомый угол, a и b — векторы, |a| и |b| — их длины, (a · b) — скалярное произведение векторов.

Если известны координаты векторов a(x1, y1) и b(x2, y2), то длины векторов и их скалярное произведение можно вычислить по следующим формулам:

• |a| = √(x1² + y1²)
• |b| = √(x2² + y2²)
• (a · b) = x1*x2 + y1*y2

После этого можно вычислить cos(α) и найти угол α через обратный косинус:

α = arccos((a · b) / (|a|*|b|))

Угол α будет выражен в радианах, поэтому его можно перевести в градусы, умножив на 180/π:

α(градусы) = α(радианы) * 180/π

Таким образом, зная координаты двух векторов на плоскости, мы можем вычислить угол между ними с помощью скалярного произведения векторов и формулы обратного косинуса.

Формула для нахождения угла

Угол — это величина, определяющая отклонение линии или поверхности от определенного направления. Для нахождения угла, необходимо знать значение косинуса или синуса данного угла.

Существует несколько формул для нахождения угла. Одна из них — формула косинуса:

cos α = adjacent / hypotenuse

где α — искомый угол, adjacent — катет примыкающий к углу, hypotenuse — гипотенуза треугольника.

Другой способ нахождения угла — использование формулы синуса:

sin α = opposite / hypotenuse

где α — искомый угол, opposite — катет противолежащий углу, hypotenuse — гипотенуза треугольника.

Также можно использовать таблицу значений тригонометрических функций для нахождения угла.

• Значение sin α для угла α может быть найдено как отношение противолежащего катета к гипотенузе треугольника.
• Значение cos α для угла α может быть найдено как отношение прилежащего катета к гипотенузе треугольника.
• Значение tg α (тангенса угла α) равно отношению противолежащего катета к прилежащему.
• Значение ctg α (котангенса угла α) равно отношению прилежащего катета к противолежащему.

Зная катеты и гипотенузу, или значения тригонометрических функций, можно легко найти угол на плоскости.

Примеры

Пусть точка A имеет координаты (2, 4) и точка B имеет координаты (6, 8). Найдем расстояние между этими точками с помощью формулы:

d = √((x2 — x1)² + (y2 — y1)²)

Подставим значения координат точек:

d = √((6 — 2)² + (8 — 4)²) = √(4² + 4²) = √32 ≈ 5,66

Таким образом, расстояние между точками A и B равно около 5,66 единиц.

Рассмотрим пример нахождения координат точки C по середине между точками A и B. Для этого воспользуемся формулами:

x = (x1 + x2) / 2, y = (y1 + y2) / 2

Подставим значения координат точек:

x = (2 + 6) / 2 = 4, y = (4 + 8) / 2 = 6

Таким образом, координаты точки C равны (4, 6).

Пример нахождения угла между осью OX и отрезком AB. Пусть координаты точки A равны (2, 4) и координаты точки B равны (6, 8). Найдем угол между отрезком AB и осью OX:

1. 1. Найдем длину отрезка AB:

d = √((6 — 2)² + (8 — 4)²) = √32 ≈ 5,66

1. 1. Найдем cos угла между отрезком AB и осью OX:

cos α = (6 — 2) / 5,66 ≈ 0,71

1. 1. Найдем угол α:

α = arccos(0,71) ≈ 45°

Таким образом, угол между отрезком AB и осью OX равен примерно 45 градусам.

Вопрос-ответ:

Какую формулу использовать для нахождения координаты точки на плоскости, зная только ее расстояние до оси OX?

Если известно только расстояние точки до оси OX, а координата OX известна, то можно использовать формулу x0±r, где x0 — координата оси OX, r — расстояние точки до оси OX, знак «+» или «-» зависит от положения точки относительно оси.

Как можно найти координаты точки, если даны координаты двух других точек и расстояния от них до искомой точки?

Для нахождения координаты точки можно использовать формулы нахождения середины отрезка и расстояния между точками. Найдем середину отрезка, соединяющего заданные точки: ((x1+x2)/2; (y1+y2)/2). Затем найдем расстояние d между этой серединой и искомой точкой, d = sqrt((x0 — (x1+x2)/2)^2 + (y0- (y1+y2)/2)^2). После этого можно решить систему уравнений для координат искомой точки.

Как определить расстояние между двумя точками на плоскости?

Расстояние между двумя точками (x1;y1) и (x2;y2) на плоскости можно найти с помощью формулы: d = sqrt((x2-x1)^2 + (y2-y1)^2).

Как определить координаты точки пересечения прямых на плоскости?

Для нахождения координат точки пересечения двух прямых на плоскости необходимо решить систему уравнений, задающих эти прямые. Общий вид уравнения прямой на плоскости: Ax+By+C=0. После решения системы можно найти координаты точки пересечения.

Как определить координаты середины отрезка на плоскости?

Координаты середины отрезка на плоскости можно найти по формуле: ((x1+x2)/2; (y1+y2)/2), где (x1;y1) и (x2;y2) — координаты концов отрезка.

Какие еще есть способы нахождения координат точки на плоскости?

Еще один способ нахождения координат точки на плоскости — использование формулы пересчета координат из полярных в декартовы. Если известны радиус и угол полярных координат точки, то можно найти ее декартовы координаты по формулам: x = r*cos(α), y = r*sin(α), где r — радиус, α — угол (измеряется в радианах).

Можно ли найти координаты точки, зная только ее расстояние до нескольких других точек на плоскости?

Да, можно. Для этого нужно взять две соединяющие искомую точку с заранее известными точками и построить их биссектрису. Точка пересечения этой биссектрисы с окружностью, радиус которой равен расстоянию между искомой точкой и одной из заданных точек, будет искомой точкой. Таким образом, остается только найти координаты точки пересечения биссектрисы и окружности.