Как правильно осуществлять переносы в математических формулах: простые правила и примеры

Узнайте, как переносить числа и математические выражения в математике. Научитесь делать это правильно и быстро, чтобы избежать ошибок и упростить расчёты. Практические советы и примеры на нашем сайте.

Математика — наука, требующая высокой точности и аккуратности. Для того, чтобы правильно решать математические задачи, важно не только знание теоретических основ, но и умение переносить числа и формулы. Ведь даже небольшая ошибка в расчете может привести к неправильному ответу.

Существует несколько методов, которые помогут легко и эффективно переносить числа и формулы в математике. Один из них — использование переносных цифр. Такой способ особенно удобен при работе с большими числами. При этом нужно очень внимательно следить за тем, к какой цифре относится переносная цифра.

Еще один метод — использование различных знаков и символов для выделения определенных частей формулы. Например, можно вычеркивать из формулы уже вычисленные значения или просто подчеркивать различные части. Это помогает сделать вычисления более наглядными и понятными.

Почему важно уметь переносить числа и формулы в математике

Перенос чисел и формул является ключевым элементом в математике, который играет важную роль в решении задач, составлении формул и сокращении времени на выполнение заданий.

Правильный перенос чисел и формул позволяет увеличить точность расчетов, что особенно важно в финансовых сферах, а также в научных и технических инженерных расчетах. Также, умение переносить числа и формулы нужно для составления уравнений и формул, что позволяет учиться математике, физике и другим наукам.

Кроме того, умение переносить числа и формулы упрощает работу с большими и сложными числами и дробями.

С помощью переноса, можно быстро и эффективно решать задачи, даже если они выглядят сложными и запутанными. Только путем переноса чисел и формул можно упростить задачи и получить правильные результаты.

В конце концов, умение переносить числа и формулы является неотъемлемой частью математической грамотности и необходимо как для школьников, так и для студентов и специалистов в высоком технологическом секторе.

В общем, умение переносить числа и формулы является важным для успеха во многих профессиональных и научных областях, и необходимо учиться этому уже на раннем этапе обучения математике.

Перенос чисел — базовые правила

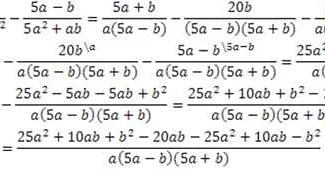
В математике перенос чисел может показаться простой задачей, однако, неверный перенос может привести к серьезным ошибкам и искажению ответа. Ниже представлены базовые правила переноса чисел в математических операциях.

Перенос чисел в сложении и вычитании

При сложении и вычитании необходимо переносить цифры в одном столбце одновременно. Например:

• 543
• + 321
• —-
• 864

В данном случае мы перенесли цифру 4 в разряд единиц, цифру 5 в разряд десятков и т.д.

Перенос чисел в умножении

При умножении лучше переносить числа по порядку, начиная с разряда меньшего числа. Например:

1. 27
2. x 36
3. —-
4. 162
5. 54
6. —-
7. 972

Здесь мы сначала умножили 6 на 7 (42) и записали результат в разряд единиц. Затем мы умножили 3 на 7 (21) и записали результат в разряд десятков. И так далее.

Перенос чисел в делении

При делении лучше использовать длинную делительную линию и переносить цифры столбиком, начиная с первого разряда числа. Например:

• 12345
• ——
• 234

Здесь мы сначала смотрим, сколько раз делитель 234 может быть внесен в число 12345. Это 52 раза. Записываем 52 на место делимого и вычитаем произведение 234 на 52 (12168) из числа 12345. Остается 1683. Затем мы переносим 8 (из 1683) на место делимого и продолжаем деление.

Запомните данные принципы и продолжайте тренировать свои навыки переноса чисел в математике.

Как переносить числа с помощью таблиц умножения

В математике часто возникают ситуации, когда необходимо быстро перенести большое число в другое место. Для этого существует множество методов, одним из которых является использование таблиц умножения.

Для переноса числа необходимо разложить его на множители и с помощью таблицы умножения перемножить один множитель на другой. Например, если нужно перенести число 425, то можно разложить его на множители 4, 2 и 5. Затем нужно найти в таблице умножения результат умножения первых двух множителей — это число 8. Далее умножаем число 8 на 5, получаем 40. Итого, число 425 можно перенести в другое место, записав его как 8 х 5 х 10^1.

Если нужно перенести число, которое не раскладывается на простые множители, то можно применить другой метод. Допустим, нужно перенести число 643. Сначала находим ближайшее к нему число, которое есть в таблице умножения, например, 648. Затем вычитаем из 648 разницу между 643 и 648, получаем в результате число 5. Далее можно записать число 643 как (648 — 5).

Используя таблицу умножения, можно быстро и эффективно переносить числа как в простых, так и в сложных случаях. Но не забывайте, что это только один из множества методов, которые существуют в математике.

Нюансы при переносе чисел с плавающей точкой

Перенос чисел с плавающей точкой — это сложный процесс, который требует внимания и аккуратности. В противном случае, мы можем получать неверный результат.

Один из важнейших нюансов при переносе чисел с плавающей точкой — это количество знаков после запятой. Необходимо убедиться, что мы переносим именно столько знаков, сколько необходимо, а не больше.

Кроме того, при переносе чисел с плавающей точкой мы также должны обратить внимание на то, какие правила округления применяются к цифрам. Возможно, нам придется округлить число до определенного знака после запятой, чтобы получить точный результат.

Прежде чем продолжать перенос чисел с плавающей точкой, нам необходимо убедиться, что у нас достаточно информации о том, какие правила округления применяются, и какое количество знаков после запятой мы должны перенести. Только после этого мы сможем быть уверенными в корректности своих вычислений.

Перенос формул: основные правила

Перенос формул – важный элемент решения математических задач. Данный метод позволяет писать формулы более компактно и удобно для восприятия. Однако, существуют некоторые правила, которые необходимо учитывать при переносе формул.

Правило №1: При переносе дробных чисел, необходимо переносить сначала числитель, а затем знаменатель. Если дробь стоит в знаменателе, то необходимо скобки добавлять, чтобы избежать ошибок.

Правило №2: Перенос многочлена осуществляется путем перемещения каждого из его членов на новую строку. Если многочлен содержит знаки «+» или «-», то знак сохраняется.

Правило №3: Перенос степенных функций осуществляется путем переноса всей функции, включая основание и показатель степени. Если функция является частью многочлена, то необходимо заключать ее в скобки.

Правило №4: При переносе под корень необходимо указывать, что корень берется из суммы. В таком случае следует писать корень над скобкой, в которой содержится сумма.

• Дополнительные правила:
• Дополнительное правило №1: При переносе формулы с индексами необходимо переместить весь индекс как единое целое.
• Дополнительное правило №2: При переносе формул с использованием квадратных скобок, необходимо сохранять скобки и заносить все элементы в новую строку.

Соблюдая данные правила, можно легко и эффективно переносить формулы и числа в математике. Этот навык пригодится при решении школьных задач и даже в профессиональной сфере.

Как переносить дроби с помощью численных примеров

Перенос дробей является важной частью математических вычислений. Нередко при решении задач нам приходится делать это много раз за одно вычисление. Перенос дробей не сложен, когда мы знаем правила, однако некоторые примеры могут быть сложными и запутывающими. Рассмотрим несколько численных примеров, чтобы понять, как легко и эффективно переносить дроби.

Пример 1:

Разложить выражение в рациональные дроби: $$\frac{1}{x^2-4}$$

Решение:

Переносим дробь, используя формулу: $$\frac{1}{a^2-b^2} = \frac{1}{(a+b)(a-b)}$$

Шаг 1:

Приводим выражение к виду $1$.

$$ \frac{1}{x^2-4} = \frac{1}{(x+2)(x-2)} $$

Пример 2:

Упростить выражение: $$\frac{3x^3+5x^2}{2x}$$

Решение:

Переносим дробь, используя формулу: $$\frac{a+b}{c} = \frac{a}{c}+\frac{b}{c}$$

Шаг 1:	Разбиваем числитель на две дроби.	$$ \frac{3x^3+5x^2}{2x} = \frac{3x^3}{2x}+\frac{5x^2}{2x} $$
Шаг 2:	Упрощаем выражение.	$$ \frac{3x^3}{2x}+\frac{5x^2}{2x} = \frac{3}{2}x^2+\frac{5}{2}x $$

Перенос дробей может быть упрощен, если мы знаем основные формулы и правила. Следуя нашим примерам, будьте внимательны и не допускайте ошибок в процессе вычислений.

Сложности при переносе логарифмов и тригонометрических функций

Перенос логарифмов и тригонометрических функций может быть сложным и требует определенных навыков и знаний. Нередко при переносе логарифмов и тригонометрических функций возникают ошибки и неточности, что может привести к неправильному решению задачи.

Основная сложность при переносе логарифмов заключается в том, что они являются функциями, обратными к экспоненциальным функциям. При переносе логарифма необходимо быть внимательным и следить за знаком, а также учитывать свойства логарифмов. Также важно помнить, что логарифм может быть выражен через экспоненту.

Перенос тригонометрических функций также требует определенных навыков и знаний. При переносе тригонометрических функций необходимо знать свойства этих функций, а также уметь приводить выражения к стандартным формам. Также при переносе тригонометрических функций необходимо учитывать знаки и косвенные функции.

Важно отметить, что при переносе логарифмов и тригонометрических функций нужно следить за точностью вычислений и правильным использованием формул. Для снижения вероятности ошибок и неточностей рекомендуется использовать ручное решение и дважды проверять все вычисления.

Перенос чисел и формул в школьной арифметике

Школьная арифметика включает в себя различные математические операции, включая сложение, вычитание, умножение и деление. При выполнении этих операций часто возникает необходимость переноса чисел и формул.

Перенос чисел является важной частью математического обучения. Он применяется в математических операциях, чтобы сделать вычисления проще и легче для понимания. Когда выполняются сложение и вычитание чисел с несколькими разрядами, необходимо переносить числа из одного разряда в другой.

При выполнении умножения и деления чисел, переносы происходят также при умножении столбиком и при делении столбиком. Чтобы выполнить эти операции, необходимо правильно переносить цифры из разряда в разряд, чтобы получить правильный ответ.

Перенос формул используется в различных областях математики, таких как алгебра и геометрия. Перенос формул позволяет решать математические задачи, которые в противном случае были бы слишком сложными для понимания.

Использование правильных методов переноса чисел и формул может значительно упростить математические операции и помочь студентам получать более высокие оценки в школьной арифметике.

Как ускорить процесс переноса в Excel

Excel — это мощное и удобное средство для работы с таблицами. Однако, каждый, кто работал с большими таблицами, сталкивался с проблемой переноса данных из одной ячейки в другую. Процесс переноса может быть медлительным и утомительным, если вы не знаете нескольких советов и трюков, позволяющих ускорить процесс.

Использование клавиатурных сочетаний

Excel имеет множество клавиатурных сочетаний, которые позволяют быстро и удобно выполнять действия, включая копирование, вставку, вырезание и перемещение данных. Например:

• Ctrl+C — копирование выделенных ячеек;
• Ctrl+V — вставка скопированных ячеек;
• Ctrl+X — вырезание выделенных ячеек;
• Ctrl+Shift+Arrow — выделение диапазона ячеек;
• Ctrl+Shift+Plus — закрытие выделенных строк или столбцов.

Знание этих сочетаний поможет вам быстро и легко работать с таблицами и переносить данные между ячейками.

Использование быстрой заполнения

Excel имеет функцию «Быстрая заполнения», которая позволяет быстро заполнить ячейки сериями, такими как даты, числа или буквы. Например, если вы ввели в ячейку «1», а затем перетянули заполнитель до ячейки «10», Excel автоматически заполнит ячейки числами от 1 до 10.

Быстрая заполнения также позволяет копировать формулы в другие ячейки и автоматически адаптировать их к новым адресам ячеек. Например, если вы ввели формулу в ячейку A1, а затем скопировали ее в ячейку B1, Excel автоматически заменит ссылки на ячейки на B1.

Использование функции «Автозаполнение»

Excel имеет функцию «Автозаполнение», которая позволяет быстро заполнить ячейки с помощью некоторых шаблонов, таких как месяцы, дни недели, числа и т.д. Например, если вы ввели январь в ячейку A1 и перетянули заполнитель до ячейки A12, Excel автоматически заполнит ячейки месяцами от января до декабря.

Также функция «Автозаполнение» позволяет заполнять ячейки с помощью пользовательских шаблонов или паттернов, что делает процесс переноса данных в Excel еще быстрее и удобнее.

Вывод

В Excel есть множество функций и трюков, которые позволяют ускорить и облегчить процесс переноса данных между ячейками. Использование клавиатурных сочетаний, быстрой заполнения и функции «Автозаполнения» — это некоторые из них. Если вы изучите эти функции и примените их в своей работе, вы значительно сократите время, затрачиваемое на перенос данных в Excel.

Популярные программы для переноса чисел и формул

Перенос чисел и формул является обязательным навыком при выполнении математических задач. Вместо ручного переписывания материала с книги или доски, многие студенты используют программы, которые помогают легко и быстро переносить числа и формулы.

Одной из таких программ является Mathpix Snipping Tool. Эта программа позволяет сканировать формулы с экрана и конвертировать их в LaTex код, который можно легко вставить в текстовый редактор или программу для создания документов. Помимо этого, программа поддерживает режим распознавания заполненных форм, благодаря чему нет необходимости копировать формулы вручную.

Другой полезной программой является Wolfram Alpha. Это огромный математический ресурс, который не только помогает переносить числа и формулы, но также предоставляет множество математических решений. Wolfram Alpha может решать уравнения, производить аналитические вычисления и строить графики. Программа доступна как браузерное приложение, а также как мобильное приложение.

Кроме того, приложение Desmos также обеспечивает простой и удобный способ создания графиков и переноса формул. Desmos помогает создавать сложные графики, а также совместно работать над проектами с помощью интерактивной доски.

В целом, использование этих программ значительно упрощает работу с математическими задачами, сокращает время, необходимое для переноса чисел и формул, и устраняет возможные ошибки при ручном переписывании.

Вопрос-ответ:

Какие существуют техники для легкого запоминания формул?

Одна из техник — это мнемотехника, когда формула ассоциируется с изображением, словами или предметами. Например, формулу «S=πr²» можно запомнить, представив себе пирог с радиусом r, который имеет площадь S. Еще одна техника — это повторение формул в разных контекстах, чтобы укрепить их в памяти.

Как легко производить вычисления в уме?

Одна из техник — это использование простых математических свойств, таких как коммутативность, ассоциативность, распределительность. Например, чтобы вычислить 16*18, можно записать это как 16*20 — 16*2, что будет проще посчитать в уме. Еще одна техника — это использование округления, чтобы более быстро получить приблизительное значение ответа.

Как избежать ошибок при переносе чисел и формул?

Одна из техник — это проверка своих вычислений, например, пересчет несколько раз. Также важно придерживаться порядка действий, который определяет правильность вычислений. Использование пометок и постепенного вычеркивания уже пройденных шагов также может помочь избежать ошибок.

Как использовать матрицы для упрощения вычислений?

Матрицы могут использоваться для работ с системами линейных уравнений, нахождения определителей и обратных матриц. Они также помогают описывать трансформации в геометрии. Для упрощения вычислений с матрицами можно использовать правила умножения матриц и свойства детерминанта.

Как использовать графики для наглядного представления математических функций?

Графики могут помочь визуализировать функции и понять их свойства, например, асимптоты, экстремумы, пересечения с осями координат. Графики могут использоваться для решения уравнений, нахождения производных, интегралов, а также для проверки правильности вычислений.

Как использовать символьные вычисления для упрощения формул?

Символьные вычисления позволяют работать с формулами в символьной форме, что упрощает алгебраические преобразования и вычисления. Например, можно использовать символьное дифференцирование и интегрирование для нахождения производных и интегралов функций, а также символьное упрощение формул для получения их более компактной и удобной формы.

Как научиться быстро решать задачи по математике?

Для быстрого решения задач по математике важно научиться выделять ключевые моменты в условии, переводить вербальные данные в математические выражения и использовать известные математические свойства и формулы. Также полезно разбить задачу на несколько более простых подзадач, поэтому важно уметь видеть общую структуру задачи и выделять ее ключевые элементы.

Как избежать ошибок при переносе и расчетах

Ошибки при переносе и расчетах — это одна из самых частых причин ошибок в математических задачах. Чтобы избежать этих ошибок, необходимо придерживаться нескольких правил.

1. Проверяйте каждый шаг

В процессе решения задачи проверяйте каждый свой шаг. Старайтесь не допускать неточностей, особенно в расчетах.

2. Отмечайте результаты

Отмечайте все результаты на каждом шаге выполнения задачи. Например, если вы посчитали промежуточный результат, напишите его сбоку, чтобы не забыть или не ошибиться.

3. Проверьте правильность переноса

Перенос числа или формулы — это еще один источник ошибок. Поэтому перед переносом проверьте тщательно правильность процедуры и данные, которые нужно перенести.

4. Пользуйтесь таблицами и графиками

Если решение задачи связано с использованием таблиц и графиков, то используйте их. Это значительно облегчит процесс переноса и расчетов.

5. Не торопитесь

Не торопитесь в процессе решения задачи. Старайтесь работать руками, чтобы не допускать опечаток и неточностей.

Соблюдая эти правила и методы, вы сможете избежать ошибок и приблизиться к успешному решению математических задач.

Видео по теме: