Механика как математическая наука оперирует

Механика в математике является наукой, изучающей движение тел и применяющей математические методы для его описания и анализа. Узнайте, как механика использует математику для предсказания, описания и объяснения физических явлений.

Механика – это раздел физики, который изучает движение и взаимодействие тел. Однако, механика также является и математической наукой, которая оперирует математическими моделями и уравнениями для описания поведения физических систем.

Основным инструментом механики является математика. Механика использует математические методы и модели для анализа движения и взаимодействия тел. Она использует математические уравнения и принципы, чтобы описать и предсказать поведение физических систем.

В механике, как и во многих других научных дисциплинах, используются различные математические методы. Одним из самых важных методов является дифференциальное и интегральное исчисление. Они позволяют анализировать изменение величин, таких как скорость и ускорение, с течением времени.

Механика также оперирует понятием вектора, который позволяет учитывать не только величину, но и направление движения. Векторы используются для описания силы, скорости и ускорения тела.

Механика также оперирует принципами сохранения энергии и импульса. Эти принципы позволяют анализировать изменение энергии и импульса тела при взаимодействии с другими телами или при изменении условий движения.

Таким образом, механика, как математическая наука, использует математические методы и модели для изучения движения и взаимодействия тел. Она оперирует понятиями вектора, дифференциального исчисления, принципов сохранения энергии и импульса, чтобы описать и предсказать поведение физических систем.

Механика: наука о движении

Механика использует математические методы для описания и предсказания движения. Она основана на нескольких основных принципах, таких как принципы Ньютона и законы сохранения. Механика позволяет не только описывать и предсказывать движение тел, но и изучать его свойства и влияние различных факторов.

Одной из важных задач механики является расчет траектории движения тела и его скорости. Для этого в механике используются различные математические модели и методы, такие как уравнения движения, интегрирование и дифференцирование.

Механика также изучает взаимодействие тел и силы, которые вызывают это взаимодействие. Взаимодействие может быть как механическим, так и гравитационным, электромагнитным, ядерным и т.д. Знание этих взаимодействий позволяет предсказывать и объяснять различные физические явления и явления в природе.

Механика находит применение в различных областях, таких как авиация, машиностроение, астрономия, физика частиц и многих других. Она играет важную роль в развитии техники и науки в целом, позволяя создавать новые устройства и технологии на основе законов и принципов механики.

Основные понятияОсновные принципы

Тело	Ньютоновская механика
Движение	Законы сохранения
Сила	Математические модели
Траектория	Уравнения движения
Скорость	Интегрирование и дифференцирование

Исторические корни механики

В средние века механика продолжала развиваться, в большей степени благодаря знаниям арабских и персидских учёных. Они разработали учение о движении, включая понятия постоянной скорости и ускорения. Однако, настоящий прорыв в развитии механики произошёл в эпоху Возрождения. Великие умы, такие как Леонардо да Винчи, Николай Коперник и Галилео Галилей, подняли механику на новый уровень, применив математический подход к изучению движения.

Впоследствии, в 17 веке, Исаак Ньютон сформулировал свои знаменитые законы движения, которые стали основой для классической механики. Ньютон также разработал концепцию гравитации и закон всемирного тяготения. С его помощью стало возможным объяснить движение планет и других небесных тел.

В 18 и 19 веках механика продолжала развиваться, привлекая к себе все больше внимания учёных. В этот период были разработаны такие важные концепции, как принцип сохранения энергии и принцип наименьшего действия. Благодаря этим открытиям механика стала все более точной и универсальной наукой, способной описывать различные физические процессы.

В 20 веке механика претерпела революционные изменения в результате развития квантовой механики и относительности. Эти новые теории изменили наше представление о мире и позволили создать более точные и объективные модели для объяснения физических явлений.

Основные законы механики

Основные законы механики включают в себя:

ЗаконОписание

Закон инерции (первый закон Ньютона)	Тело сохраняет свое состояние покоя или равномерного прямолинейного движения, пока на него не действует внешняя сила.
Закон динамики (второй закон Ньютона)	Ускорение тела прямо пропорционально приложенной силе и обратно пропорционально его массе.
Закон взаимодействия (третий закон Ньютона)	Для каждого действия существует равное по величине и противоположно направленное противодействие.

Эти законы являются основой для понимания и анализа движения тел в механике. Они позволяют предсказывать поведение тел в различных физических системах и применяются во многих областях, включая инженерию, физику, астрономию и другие науки.

Динамика и статика: различия и приложения

Основное отличие между динамикой и статикой заключается в том, что динамика изучает движение тел, включая изменение скорости и направления движения, а статика изучает равновесие тел, когда сумма всех действующих сил равна нулю и тело находится в покое или движется с постоянной скоростью.

Динамика и статика имеют различные приложения в реальном мире. Динамика применяется для изучения движения объектов, таких как автомобили, самолеты, спутники и другие тела, движущиеся под воздействием различных сил. Она также используется для анализа и проектирования механических систем, таких как машины и конструкции.

Статика, с другой стороны, применяется для изучения равновесия объектов и анализа систем, в которых силы компенсируют друг друга. Это может быть полезно при проектировании зданий и мостов, чтобы обеспечить их стабильность и безопасность. Статика также используется для расчета нагрузок на материалы, такие как стержни и балки, и для определения сил, действующих на различные элементы конструкций.

Изучение динамики и статики является важным для понимания поведения физических систем и разработки новых технологий. Оно помогает инженерам и ученым прогнозировать и оптимизировать работу механических систем и создавать более эффективные и безопасные конструкции.

Кинематика: изучение движения без причин

Основной задачей кинематики является описание движения объектов с помощью определенных параметров и их соотношений. Для этого используются различные математические методы, включая графики, таблицы и формулы.

Основные понятия кинематики:

ПонятиеОписание

Время	Величина, отражающая последовательность событий и изменений в процессе движения.
Положение	Место, где находится тело в определенный момент времени. Обычно задается величиной координаты.
Скорость	Величина, характеризующая изменение положения за единицу времени. Может быть постоянной или изменяться со временем.
Ускорение	Величина, характеризующая изменение скорости за единицу времени. Может быть постоянным или изменяться со временем.

Используя эти понятия, кинематика позволяет описать и предсказать движение объектов в пространстве и времени. Она находит применение в различных областях, таких как физика, инженерия, астрономия и другие.

Несмотря на то, что кинематика не учитывает причины движения, она является необходимым инструментом для понимания и анализа механических систем. Без кинематики было бы невозможно изучать и описывать движение объектов и разрабатывать эффективные решения в различных областях науки и техники.

Математическое описание движения

Механика, как математическая наука, обладает инструментарием для математического описания движения. Для этого используются различные математические понятия и формулы.

Описание движения в механике основывается на двух основных понятиях: позиции и времени. Позиция объекта в пространстве может быть описана с помощью координат. Для простого одномерного движения используется одна координата, а для сложного движения в трехмерном пространстве используются три координаты.

Для математического описания движения используются формулы, основанные на законах Ньютона. Закон Ньютона описывает связь между силой, массой и ускорением объекта. Формула второго закона Ньютона выглядит следующим образом: F = ma, где F — сила, m — масса объекта, а — ускорение.

Для описания движения в задачах механики часто используются такие понятия, как скорость и ускорение. Скорость — это изменение позиции объекта по времени. Ускорение — это изменение скорости по времени.

Для описания движения с постоянной скоростью используется формула s = vt, где s — путь, v — скорость, t — время. Для описания движения с постоянным ускорением используется формула s = ut + (at^2)/2, где u — начальная скорость, a — ускорение, t — время.

ФормулаОписание

F = ma	Закон Ньютона о связи силы, массы и ускорения
s = vt	Формула для движения с постоянной скоростью
s = ut + (at^2)/2	Формула для движения с постоянным ускорением

Математическое описание движения позволяет решать различные задачи, связанные с движением объектов. Путем анализа и применения соответствующих формул можно получить информацию о скорости, ускорении, времени, дистанции и других параметрах движения.

Решение задач механики с помощью математики

Один из ключевых инструментов, используемых при решении задач механики, — это математический аппарат. С помощью математических методов можно описать движение тел, определить их скорость, ускорение, силы, энергию и другие величины.

Для решения задач механики применяются различные математические подходы, включая дифференциальное и интегральное исчисление, алгебру, геометрию и теорию вероятностей. При решении задач могут использоваться уравнения движения, законы сохранения энергии и импульса, принципы динамики и другие математические выкладки.

Часто решение задач механики предполагает построение графиков, таблиц и диаграмм, которые помогают визуализировать и анализировать полученные результаты. Для этого часто используется таблица с данными о движении тела, включающая время, координаты, скорость, ускорение и другие параметры.

Также для решения задач механики могут применяться принципы и методы математического моделирования. Математические модели позволяют абстрагироваться от реальных объектов и явлений, исследовать их свойства и получать количественные результаты.

В итоге, решение задач механики с помощью математики позволяет получить точные и количественные результаты, а также провести анализ и прогнозирование движения тел. Математика является неотъемлемой частью механики и позволяет достичь глубокого понимания законов и принципов, определяющих движение тел в пространстве и времени.

Видео по теме:

Вопрос-ответ:

Какая роль в механике играет математика?

Математика играет ключевую роль в механике, так как она позволяет формализовать и описать физические законы и явления. Благодаря математическим моделям, мы можем прогнозировать движение тел, рассчитывать силы, скорости, ускорения и другие физические величины.

Какие математические методы используются в механике?

В механике используются различные математические методы, такие как дифференциальное и интегральное исчисление, алгебра, геометрия и теория вероятностей. Эти методы позволяют анализировать и решать сложные задачи, связанные с движением и взаимодействием тел.

Как математика помогает прогнозировать движение тел?

Математика позволяет построить математические модели, которые описывают движение тел. С помощью уравнений и формул, основанных на законах физики, можно рассчитать скорости, ускорения, траектории и другие характеристики движения. Такие модели позволяют прогнозировать будущее положение и состояние тела в определенный момент времени.

Какие примеры применения математики в механике?

Примеры применения математики в механике есть везде: от простых расчетов силы тяжести до сложных задач аэродинамики и космических полетов. Например, математические модели используются для расчета траекторий падения тел, проектирования автомобильных двигателей, анализа сил и деформаций в строительных конструкциях и многого другого. Математика является неотъемлемой частью механики и помогает ей развиваться и прогрессировать.

Какие проблемы решает математика в механике?

Математика в механике решает множество различных проблем, связанных с движением и взаимодействием тел. Она помогает рассчитывать силы и ускорения, определять траектории движения, анализировать статику и динамику систем, моделировать физические процессы и многое другое. Математика позволяет нам понять и объяснить законы природы, которые лежат в основе механики.

Что такое механика?

Механика — это раздел физики, который изучает движение и взаимодействие тел, а также причины, которые его вызывают.

Механические системы и их классификация

Механические системы можно классифицировать по разным критериям. Одним из основных критериев является количество степеней свободы системы. Степень свободы — это количество независимых перемещений, необходимых для описания положения системы в пространстве.

Согласно этому критерию механические системы делятся на:

• Одностепенные системы. В таких системах объекты могут перемещаться только в одной плоскости или по одной прямой.
• Двухстепенные системы. В таких системах объекты могут перемещаться в двух плоскостях или по двум прямым.
• Многостепенные системы. В таких системах объекты могут перемещаться в трех и более плоскостях или по трех и более прямым.

Еще одним критерием классификации является характер взаимодействия между объектами в системе. В зависимости от этого механические системы делятся на:

• Закрытые системы. В таких системах объекты взаимодействуют только друг с другом и не взаимодействуют с внешней средой.
• Открытые системы. В таких системах объекты взаимодействуют как друг с другом, так и с внешней средой.

Таким образом, классификация механических систем позволяет более точно определить их свойства и особенности, что важно для разработки и анализа различных технических устройств и конструкций.

Применение механики в различных областях науки и техники

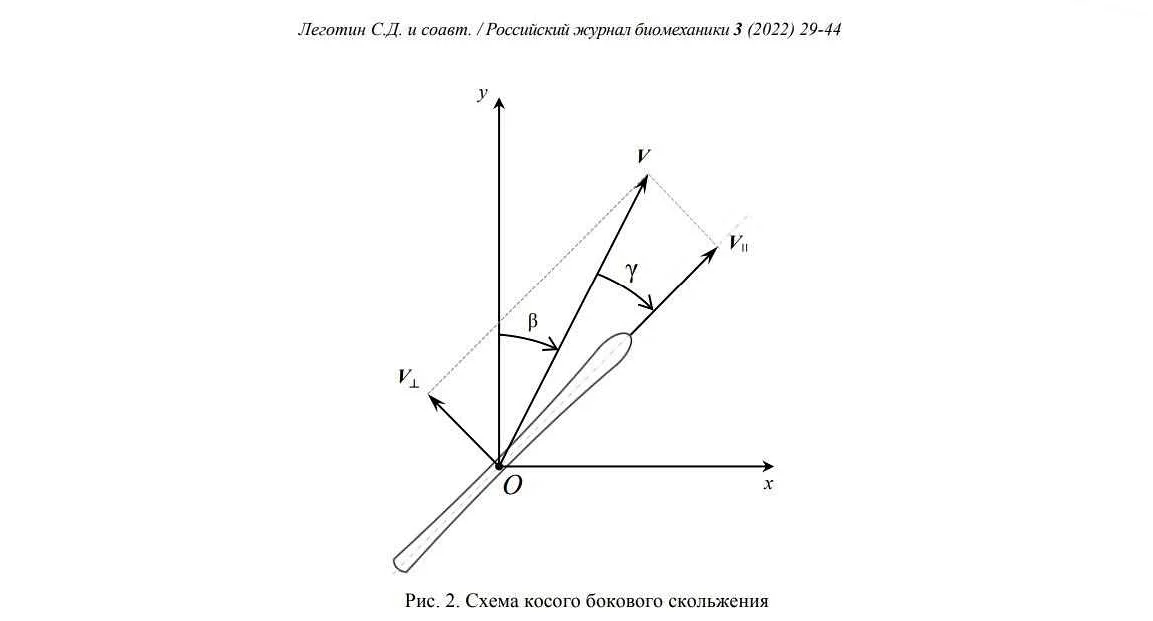
Механика, как математическая наука, имеет широкое применение в различных областях науки и техники. Ее основные принципы и законы могут быть применены для изучения и описания различных физических явлений и процессов.

В области физики, механика используется для исследования движения тел и объяснения причин их движения. С помощью механики можно определить траекторию движения объекта, его скорость и ускорение. Это позволяет предсказывать поведение объектов в различных условиях и разрабатывать модели, которые помогают в понимании многих физических явлений.

Механика также находит применение в астрономии. Она помогает исследователям изучать движение планет, звезд и других небесных объектов. Законы механики позволяют предсказывать и объяснять феномены, такие как гравитация, орбиты планет и спутников, и даже расшифровывать сигналы от удаленных галактик.

В инженерии механика играет важную роль в разработке и конструировании различных механизмов и машин. Законы механики помогают инженерам определить оптимальный дизайн и конструкцию объектов, чтобы они были безопасными и эффективными в работе. Механика также используется для исследования и разработки новых материалов со специфическими свойствами, которые могут быть использованы в различных отраслях техники.

Применение механики также находит в медицине. Механические принципы используются для изучения и моделирования работы человеческого организма. Например, механика позволяет исследовать работу сердца и кровеносной системы, определять условия, при которых они функционируют нормально, а также разрабатывать и тестировать искусственные органы и протезы.

Таким образом, механика является фундаментальной наукой, которая имеет широкое применение в различных областях науки и техники. Ее основные принципы и законы помогают исследователям и инженерам понимать и описывать физические явления, разрабатывать новые технологии и улучшать существующие устройства и процессы.