Математическая модель которая описывает поведение и свойства объекта только в отдельные моменты

Математическая модель, описывающая поведение и характеристики объекта только в определенные моменты времени. Интересная статья о применении дискретных моделей в науке и технике.

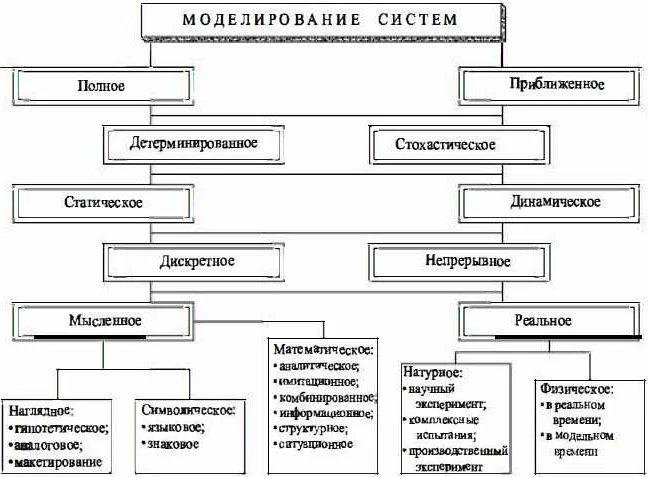
Математические модели играют важную роль в науке и инженерии, помогая нам понять, описать и предсказать поведение объектов в различных ситуациях. Одной из основных задач моделирования является создание математической модели, которая бы описывала поведение и свойства объекта в отдельные моменты времени.

Модель может быть представлена в виде уравнений и формул, которые описывают зависимости между различными переменными и параметрами объекта. В процессе моделирования мы учитываем такие факторы, как физические законы, исходные данные, условия и ограничения.

Полученные модели позволяют нам анализировать поведение объекта в различных ситуациях и предсказывать его свойства в определенные моменты времени. Например, математическая модель может помочь определить траекторию движения объекта, его скорость, ускорение и другие параметры.

Математическое моделирование играет важную роль в различных областях науки и техники, таких как физика, экономика, биология, инженерия и другие. Оно позволяет нам лучше понять исследуемый объект, предсказать его поведение и принять обоснованные решения на основе полученных результатов.

Математическая модель объекта и его свойства

Математическая модель представляет собой абстракцию реального объекта, которая описывает его поведение и свойства в определенные моменты времени. Эта модель может быть представлена в виде математических уравнений, функций или систем уравнений, которые описывают взаимодействие различных компонентов объекта.

Математическая модель позволяет анализировать и предсказывать поведение объекта в различных ситуациях. Она позволяет изучать его свойства, оптимизировать его работу, улучшить производительность и снизить затраты.

В математической модели объекта могут учитываться различные факторы и переменные, такие как время, температура, давление, скорость и другие параметры, которые влияют на его поведение и свойства.

Разработка математической модели объекта требует глубокого понимания его структуры и принципов работы. Она может быть основана на физических законах, статистических данных, эмпирических наблюдениях или других источниках информации.

Математическая модель объекта и его свойства позволяют исследовать различные сценарии и ситуации, предсказывать результаты и принимать обоснованные решения. Они широко применяются в различных областях, таких как физика, экономика, биология, инженерия и другие.

Использование математической модели объекта и его свойств позволяет значительно улучшить процессы проектирования, оптимизации и управления объектами, повысить эффективность и достигнуть поставленных целей.

Видео по теме:

Определение и назначение модели

Основное назначение модели состоит в анализе и прогнозировании характеристик объекта или системы. Путем построения математических моделей можно исследовать различные сценарии и предсказывать результаты их изменений. Модели помогают понять взаимосвязи между различными переменными и оптимизировать процессы или принимать решения на основе полученных данных.

Математические модели широко используются в различных областях, таких как физика, химия, экономика, биология и техника. Они помогают упростить сложные явления и системы, исследовать их свойства и предсказать результаты экспериментов.

Преимущества использования математических моделей:Недостатки использования математических моделей:

Позволяют анализировать и прогнозировать поведение объекта или системы	Могут быть сложными и требовать высокой математической подготовки для их построения и анализа
Упрощают сложные явления и помогают выявить ключевые факторы	Могут быть ограничены в точности и неполными в описании реальности
Позволяют проводить виртуальные эксперименты и исследования	Могут быть зависимы от точности и доступности данных для построения модели

Использование математических моделей является важным инструментом для научных исследований, инженерных расчетов и принятия решений в различных областях. Они позволяют предсказывать результаты, оптимизировать процессы и разрабатывать новые решения на основе анализа и моделирования объекта или системы.

Важность математической модели для понимания объекта

Математическая модель позволяет абстрагироваться от реального объекта и сосредоточиться на его ключевых характеристиках. Она представляет объект в виде математических уравнений, формул и алгоритмов, которые описывают его поведение и свойства. Это позволяет исследователям более глубоко и точно изучать объект и его взаимодействие с окружающей средой.

Математическая модель также обладает преимуществом предсказательной силы. Она позволяет проводить эксперименты в виртуальной среде и предсказывать результаты в реальной жизни. Это позволяет сэкономить время и ресурсы на проведении физических экспериментов и исследований.

Кроме того, математическая модель позволяет проводить анализ и оптимизацию исследуемых процессов и систем. Она позволяет определить оптимальные значения параметров и условий, которые приведут к наилучшему результату. Это особенно важно при проектировании и управлении сложными системами, где необходимо учесть большое количество факторов и ограничений.

Таким образом, математическая модель является неотъемлемой частью научных и инженерных исследований. Она позволяет более глубоко понять объект и его свойства, предсказать его поведение и провести анализ и оптимизацию исследуемых явлений и процессов.

Вопрос-ответ:

Какую математическую модель можно использовать для описания поведения объекта в отдельные моменты?

Для описания поведения объекта в отдельные моменты можно использовать различные математические модели, в зависимости от конкретной ситуации и характеристик объекта. Например, в случае динамических систем можно применять дифференциальные уравнения или разностные уравнения. В случае статических систем можно использовать алгебраические уравнения или вероятностные модели. Важно выбрать подходящую модель, которая наилучшим образом отражает особенности объекта и позволяет достичь требуемой точности предсказания его поведения.

Какие свойства объекта могут быть учтены в математической модели его поведения в отдельные моменты?

Математическая модель поведения объекта в отдельные моменты может учитывать различные свойства объекта. Например, это могут быть его физические характеристики, такие как масса, скорость, ускорение и сила, его геометрические параметры, такие как размеры и форма, а также параметры, связанные с его окружением и внешними воздействиями. В зависимости от конкретной задачи и объекта, которые нужно решить, в модель могут быть включены различные свойства, чтобы достичь наилучшего предсказания поведения объекта в отдельные моменты.

Каким образом математическая модель может быть использована для предсказания поведения объекта в отдельные моменты?

Математическая модель может быть использована для предсказания поведения объекта в отдельные моменты путем решения соответствующих математических уравнений, которые описывают его поведение. Например, если объект является динамической системой, то можно использовать дифференциальные уравнения или разностные уравнения, чтобы определить его состояние в определенный момент времени на основе его предыдущего состояния и внешних воздействий. Если объект является статической системой, то можно использовать алгебраические уравнения или вероятностные модели для предсказания его поведения. Важно правильно сформулировать и решить уравнения, чтобы получить достоверное предсказание поведения объекта.

Какую роль играет математическая модель в изучении поведения и свойств объекта?

Математическая модель позволяет упростить сложную реальность и анализировать поведение и свойства объекта в отдельные моменты времени. Она является инструментом для исследования, прогнозирования и оптимизации, а также помогает улучшить понимание объекта и его взаимодействия с внешней средой.

Какую информацию можно получить с помощью математической модели?

С помощью математической модели можно получить разнообразную информацию о поведении и свойствах объекта. Например, можно определить оптимальные параметры объекта, предсказать его будущее состояние, оценить влияние различных факторов на его работу, а также проанализировать его взаимодействие с другими объектами и окружающей средой.

Формирование математической модели

Процесс формирования математической модели включает несколько этапов. Вначале необходимо определить цель моделирования и установить связь между объектом и его математическим описанием. Затем происходит выбор математических методов и модельных уравнений, которые наилучшим образом отражают поведение и свойства объекта. При этом учитываются все важные факторы и условия, которые могут влиять на поведение объекта.

После выбора модельных уравнений происходит их анализ и решение. На этом этапе проводятся математические вычисления и аппроксимации, чтобы получить численные значения и характеристики объекта. В завершение процесса формирования математической модели происходит проверка полученных результатов и их интерпретация, чтобы оценить соответствие модели реальному объекту и его свойствам.

Формирование математической модели позволяет не только лучше понять объект и его поведение, но и предсказать его будущее поведение. Математическая модель может быть использована для оптимизации процессов, прогнозирования результатов и принятия решений. Она является мощным инструментом в науке, технике и других областях, где требуется анализ и исследование сложных систем и явлений.

Основные компоненты математической модели

Математическая модель представляет собой абстракцию реального объекта или явления, которая использует математические понятия и методы для его описания и анализа. Основные компоненты математической модели включают:

1. Переменные: это символы, которые представляют измеряемые или наблюдаемые характеристики объекта или явления. Они могут быть числами, функциями или другими математическими выражениями.

2. Параметры: это символы, которые представляют неизвестные или изменяемые характеристики объекта или явления. Значения параметров могут быть определены экспериментально или заданы на основе предыдущих исследований.

3. Уравнения: это математические выражения, которые связывают переменные и параметры в модели. Уравнения описывают зависимости и взаимодействия между компонентами модели.

4. Интерпретация: это процесс определения значений переменных и параметров модели на основе имеющихся данных или экспериментов. Интерпретация позволяет использовать модель для предсказания поведения объекта или явления в различных ситуациях.

5. Валидация: это процесс проверки достоверности и точности модели путем сравнения ее результатов с экспериментальными данными или другими независимыми источниками информации.

Все эти компоненты взаимодействуют между собой и определяют структуру и свойства математической модели. Создание и использование математических моделей позволяет анализировать и предсказывать поведение объектов и явлений, что является важным инструментом в научных и инженерных исследованиях.

Применение математической модели для анализа и прогнозирования

Одним из основных преимуществ математической модели является ее точность и надежность. Модель основывается на строгих математических принципах и позволяет проводить анализ с высокой степенью точности. Благодаря этому, модель может быть использована для прогнозирования с высокой степенью вероятности.

Применение математической модели позволяет производить анализ различных параметров и свойств объекта. Модель может учитывать различные факторы и взаимосвязи между ними, что позволяет получить полную картину их влияния на поведение объекта. Это позволяет проводить глубокий анализ и выявлять скрытые закономерности и зависимости.

Прогнозирование с помощью математической модели позволяет предсказывать тенденции и направление развития объекта. Модель может быть использована для прогнозирования будущих значений параметров и свойств объекта, а также для определения оптимальных стратегий и решений. Благодаря этому, модель может быть применена в различных областях, таких как экономика, финансы, наука и технологии.

Валидация и верификация математической модели

Верификация же представляет собой процесс проверки математической модели на соответствие ее математическому описанию и требованиям, предъявляемым к этой модели. Верификация позволяет убедиться в том, что модель разработана правильно и соответствует заложенным в нее математическим законам и принципам. Таким образом, верификация помогает установить корректность модели с точки зрения математического описания.

Оба процесса валидации и верификации важны для достижения надежности и точности математической модели. Они позволяют убедиться в том, что модель является адекватным описанием реального объекта, а также соответствует требованиям, предъявляемым к ней. Валидация и верификация математической модели помогают установить ее правильность и достоверность, что в свою очередь позволяет использовать модель для решения практических задач и принятия решений.

В процессе валидации и верификации математической модели применяются различные методы и подходы. Они включают в себя проведение экспериментов, сравнение результатов моделирования с экспериментальными данными, анализ математических свойств модели и другие методы. От результатов валидации и верификации зависит степень доверия к математической модели и возможность ее использования для решения практических задач.

Ограничения и предположения математической модели

Одним из ограничений математической модели является предположение о линейности. В реальности многие объекты и явления не являются линейными, но математическая модель может предполагать, что они таковы. Это может привести к неточным результатам или неправильным выводам, особенно при моделировании сложных систем.

Другим ограничением является предположение о стационарности. Математическая модель может предполагать, что свойства объекта не меняются со временем и остаются постоянными. В реальности это далеко не всегда верно, и модель может не учитывать изменения в поведении объекта со временем.

Также математическая модель может иметь ограничения на точность данных. Модель может базироваться на определенных данных или измерениях, которые могут быть неполными или неточными. Это может приводить к неточностям и погрешностям в результатах моделирования.

Еще одним ограничением является предположение о независимости переменных. Математическая модель может предполагать, что переменные влияют на результаты независимо друг от друга. В реальности переменные могут быть взаимосвязаны, и это может привести к неточностям в моделировании.

Важно учитывать эти ограничения и предположения при использовании математической модели, чтобы оценивать ее результаты с учетом реальной ситуации и не делать неправильных выводов или прогнозов.

Примеры успешного использования математических моделей

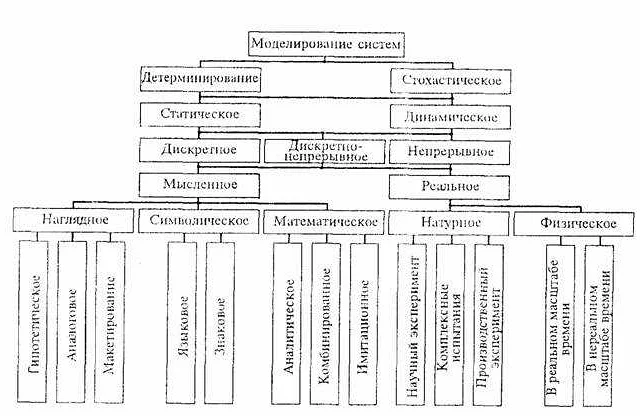
Математические модели широко используются в различных областях науки и техники. Они позволяют предсказывать поведение и свойства объектов в отдельные моменты и помогают принимать взвешенные решения на основе полученных данных. Вот несколько примеров успешного использования математических моделей:

1. В экономике. Математические модели помогают анализировать финансовые рынки, прогнозировать изменения цен на акции и товары, оптимизировать инвестиционные портфели.
2. В медицине. Математические модели используются для изучения распространения инфекционных заболеваний, предсказания эффективности новых лекарств и проведения клинических испытаний.
3. В транспорте. Математические модели позволяют оптимизировать маршруты движения транспортных средств, улучшить организацию городского движения, снизить затраты на топливо.
4. В экологии. Математические модели используются для прогнозирования изменений климата, изучения воздействия человеческой деятельности на экосистемы и разработки мер по их сохранению.
5. В инженерии. Математические модели помогают проектировать и симулировать работу сложных систем, таких как авиационные двигатели, электронные устройства и производственные цехи.

Это лишь некоторые примеры успешного использования математических моделей. Уникальность и мощь математических моделей заключается в их способности описывать и предсказывать сложные явления и процессы, которые не всегда могут быть полностью поняты на интуитивном уровне.