Математика как найти х
Содержимое
- 1 Математика как найти х
- 1.1 Метод подстановки
- 1.2 Метод пристального взгляда
- 1.3 Метод интерполяции
- 1.4 Метод дихотомии
- 1.5 Метод Ньютона
- 1.6 Вопрос-ответ:
- 1.6.0.1 Какие основные методы и приемы можно использовать для решения математических задач?
- 1.6.0.2 Как найти значение неизвестной переменной в математической формуле?
- 1.6.0.3 Как можно найти корни квадратного уравнения?
- 1.6.0.4 Как найти решение системы линейных уравнений?
- 1.6.0.5 Как найти значение неизвестной переменной в функции?
- 1.6.0.6 Как найти неизвестное значение х в математике?
- 1.7 Метод простых итераций
- 1.8 Видео по теме:
Узнайте, как использовать математику для поиска неизвестного значения х в уравнениях и задачах. Наша статья предлагает простые и понятные объяснения, а также методы решения, которые помогут вам найти значение х с легкостью.
Поиск неизвестных значений, таких как х, является одной из основных задач математики. Этот процесс изучается в школьной программе и используется в реальной жизни для решения различных задач. На первый взгляд, поиск х может показаться сложным и запутанным, но на самом деле существуют несколько основных методов и приемов, которые помогут вам найти неизвестное значение.
Один из наиболее распространенных методов — уравнения. Уравнение представляет собой математическое выражение, в котором неизвестное значение обозначается буквой х. Чтобы найти х, необходимо преобразовать уравнение, выполнив определенные действия. При этом важно помнить, что все операции, выполняемые на одной стороне уравнения, должны быть выполнены и на другой стороне, чтобы сохранить его равенство.
Еще одним полезным методом является подстановка. Если в уравнении присутствуют конкретные значения, можно подставить их вместо х и решить уравнение. Этот метод особенно полезен, когда в уравнении присутствует только одно неизвестное значение. Однако, если в уравнении более одного неизвестного значения, подстановка может быть затруднительна.
Другим методом, часто используемым для поиска х, является графическое представление. Построение графика функции или уравнения позволяет визуально определить значение х. Для этого необходимо построить график на координатной плоскости и найти точку пересечения графика с осью, на которой находится х.
Независимо от выбранного метода, важно помнить, что поиск х в математике требует внимательности и точности. Небольшая ошибка в расчетах может привести к неверному результату. Поэтому рекомендуется выполнять все действия поэтапно и проверять полученный ответ.
Метод подстановки
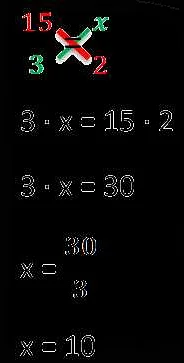
Применение метода подстановки позволяет найти значение неизвестной переменной, заменив ее значением известной переменной или выражением.
Для применения метода подстановки необходимо:
- Выбрать известную переменную или выражение, с помощью которых можно выразить неизвестную переменную.
- Подставить значение известной переменной или выражения в уравнение.
- Решить полученное уравнение относительно неизвестной переменной.
- Проверить полученное значение, подставив его в исходное уравнение.
Применение метода подстановки позволяет решать как простые, так и сложные уравнения. Он может быть полезен при решении систем уравнений или подсчете значений функций.
Метод подстановки является одним из базовых инструментов математики и широко применяется в различных областях, где требуется нахождение значений переменных или функций.
Метод пристального взгляда
Основная идея метода заключается в том, чтобы рассмотреть все имеющиеся данные, поставить перед собой вопросы и постараться выявить связи и закономерности. Важно обратить особое внимание на условия задачи, наличие известных данных и ограничений.
Для применения метода пристального взгляда необходимо внимательно прочитать условие задачи, разобраться в его содержании и выделить ключевые моменты. Затем следует провести анализ доступных данных, изучить связи между ними и пометить важные детали.
Следующим шагом является формулирование гипотезы о возможном значении неизвестной величины х. Для этого необходимо внимательно проанализировать данные и вывести возможные закономерности или связи между ними. Гипотезы могут быть различными, и важно рассмотреть все возможные варианты.
После формулирования гипотезы следует провести проверку, сравнивая ее с известными данными и условиями задачи. Если гипотеза подтверждается, то найденное значение х вероятно является правильным. Если же гипотеза не подтверждается, необходимо вернуться к анализу данных и поискать другие возможные связи или закономерности.
Метод пристального взгляда требует внимательности, логического мышления и тщательного анализа данных. Он позволяет исследовать математические задачи с разных сторон и найти нетривиальные решения.
Метод интерполяции

Основная идея метода интерполяции заключается в том, чтобы аппроксимировать функцию с помощью некоторого класса интерполяционных функций, и затем использовать эти функции для нахождения значения неизвестной переменной внутри заданного интервала.
Существует несколько различных методов интерполяции, таких как линейная интерполяция, кубическая интерполяция и сплайн-интерполяция. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях.
При использовании метода интерполяции необходимо учитывать ограничения и предположения, которые вносятся в процесс интерполяции. Например, интерполяция может быть менее точной на границах диапазона значений, и результаты могут быть искажены при использовании интерполяции для экстраполяции.
Метод интерполяции широко применяется в различных областях, включая математику, физику, экономику и компьютерную графику. Он позволяет получить более гладкие и непрерывные значения функции, основываясь на ограниченном наборе известных значений.
Метод дихотомии
Прежде всего, для применения метода дихотомии необходимо знать, что функция, в которой ищется корень, должна быть непрерывной и монотонной на заданном интервале. Также необходимо иметь начальное приближение корня, то есть знать интервал, в котором находится корень.
Алгоритм метода дихотомии следующий:
- Выбирается начальный интервал, в котором находится корень. Для этого используются начальные приближения. Начальный интервал делится пополам.
- Вычисляется значение функции в середине интервала.
- На основе знака значения функции определяется, в какой половине интервала находится корень.
- Половина интервала, в которой находится корень, становится новым интервалом.
- Шаги 2-4 повторяются до тех пор, пока интервал не станет достаточно малым, то есть пока его длина не станет меньше заданной точности.
Метод дихотомии гарантирует нахождение корня с заданной точностью, однако требует большого числа итераций, особенно при поиске корней функций с низкой крутизной. Тем не менее, этот метод широко используется из-за своей простоты и надежности.
Важно отметить, что метод дихотомии можно применять не только для нахождения корней уравнений, но и для нахождения точек минимума или максимума функций. В этом случае необходимо анализировать значения функции не на знак, а на возрастание или убывание.
Метод Ньютона
Идея метода Ньютона заключается в построении касательной линии к графику функции и нахождении точки пересечения касательной с осью абсцисс. Получившаяся точка является приближенным значением корня уравнения.
Математический алгоритм метода Ньютона выглядит следующим образом:
- Выбрать начальное приближение x0.
- Вычислить значение функции f(x) и её производной f'(x) в точке x0.
- Вычислить следующее приближение x1 по формуле: x1 = x0 — f(x0) / f'(x0).
- Повторять шаги 2-3 до достижения заданной точности или достижения максимального количества итераций.
Метод Ньютона обладает быстрой сходимостью к корню функции, особенно при хорошем начальном приближении. Однако, он может не сходиться или сходиться к другим корням функции, если начальное приближение выбрано неправильно.
Важно отметить, что метод Ньютона требует наличия производной функции, поэтому он не применим к функциям без производной или к функциям с разрывами производной.
Вопрос-ответ:
Какие основные методы и приемы можно использовать для решения математических задач?
Основные методы и приемы для решения математических задач включают в себя использование алгоритмов, применение логических рассуждений, использование математических формул и теорем, а также анализ и синтез данных. Кроме того, можно использовать графические и численные методы для нахождения решений.
Как найти значение неизвестной переменной в математической формуле?
Для нахождения значения неизвестной переменной в математической формуле можно использовать методы аналитической геометрии, алгебры, и численные методы. Аналитическая геометрия позволяет находить значения переменных с помощью графического представления уравнений, а алгебраические методы позволяют решать уравнения и системы уравнений для нахождения значений переменных. Численные методы используются, когда аналитические методы решения не пригодны или неэффективны.
Как можно найти корни квадратного уравнения?
Для нахождения корней квадратного уравнения можно использовать формулу дискриминанта. Дискриминант определяется как D = b^2 — 4ac, где a, b и c — коэффициенты квадратного уравнения. Если дискриминант положителен, то уравнение имеет два различных вещественных корня. Если дискриминант равен нулю, то уравнение имеет один корень. Если дискриминант отрицателен, то уравнение имеет два комплексных корня.
Как найти решение системы линейных уравнений?
Для нахождения решения системы линейных уравнений можно использовать метод Гаусса-Жордана или метод Крамера. Метод Гаусса-Жордана заключается в последовательном преобразовании системы уравнений и приведении ее к треугольному виду, после чего можно найти значения переменных. Метод Крамера использует определители матрицы коэффициентов системы уравнений для нахождения значений переменных. Оба метода могут быть применены в зависимости от конкретной системы уравнений.
Как найти значение неизвестной переменной в функции?
Для нахождения значения неизвестной переменной в функции необходимо подставить значение переменной вместо нее в выражение функции и выполнить вычисления. Например, если функция f(x) = 2x + 5, чтобы найти значение f(3), нужно подставить 3 вместо х в эту функцию: f(3) = 2 * 3 + 5 = 6 + 5 = 11. Таким образом, значение f(3) равно 11.
Как найти неизвестное значение х в математике?
Для нахождения неизвестного значения х в математике существуют различные методы и приемы, в зависимости от типа задачи. Например, для решения уравнений используются методы подстановки, преобразования и графического исследования. В задачах с пропорциями используется метод перекрестного умножения. Также в математике применяются методы интерполяции и экстраполяции для определения значения х в заданном диапазоне. Важно помнить, что для решения математических задач требуется уверенное владение базовыми математическими операциями и понимание соответствующих правил и свойств чисел.
Метод простых итераций

Для применения метода простых итераций необходимо:
- Задать уравнение, в котором нужно найти корень: f(x) = 0
- Преобразовать уравнение так, чтобы x находилось в правой части: x = g(x)
- Выбрать начальное приближение x0
- Найти следующее приближение x1, подставив x0 в функцию g(x): x1 = g(x0)
- Повторять шаг 4 до достижения необходимой точности или сходимости
Метод простых итераций подходит для широкого класса уравнений, включая нелинейные и системы уравнений. Однако, для обеспечения сходимости и точности результатов необходимо правильно выбирать функцию g(x) и начальное приближение x0.
Для ускорения сходимости и повышения точности метода простых итераций можно использовать различные приемы, такие как метод Ньютона-Рафсона или метод секущих.
ПреимуществаНедостатки
| Простота реализации | Медленная сходимость |
| Широкий класс применимости | Зависимость от выбора начального приближения и функции g(x) |
| Возможность применения к системам уравнений | Потеря точности при большом количестве итераций |
В заключение, метод простых итераций является важным инструментом в математике и нахождении корней уравнений. Он обладает своими преимуществами и недостатками, и требует тщательного выбора параметров для достижения нужной точности результатов.
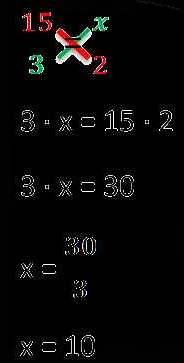



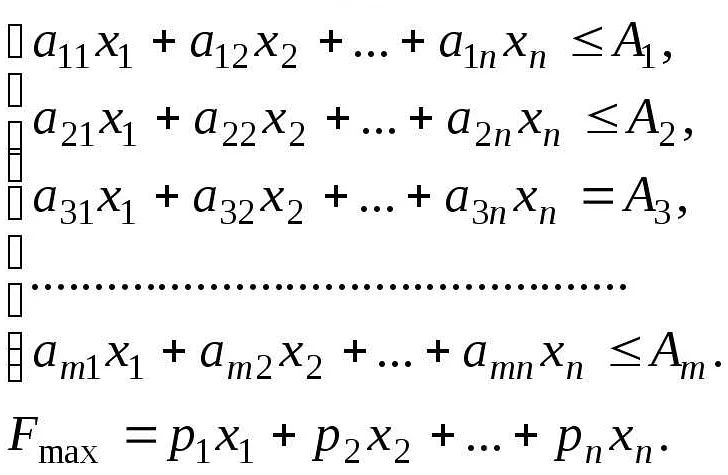
Статья очень полезна и информативна! Я всегда сталкиваюсь с проблемой поиска неизвестного х в математике, и этот материал помог мне разобраться с основными методами и приемами. Теперь я знаю, что первым шагом нужно выразить х через известные величины, а затем использовать алгебраические операции для решения уравнений. Также автор подробно описал методы подстановки и приведения подобных слагаемых, которые помогут найти корень уравнения. Я особенно оценил примеры и пояснения, которые позволяют легче усвоить материал. Отличная статья, я теперь чувствую себя увереннее в решении математических задач!