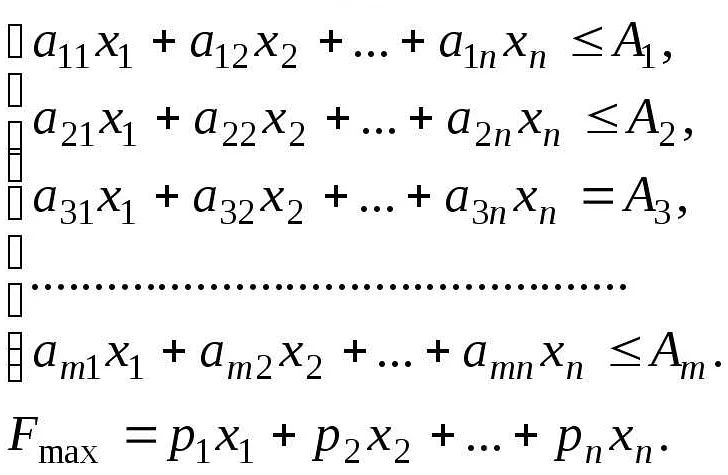Группы неизвестных величин в экономико-математической модели: как определить и применить
Содержимое
- 1 Группы неизвестных величин в экономико-математической модели: как определить и применить
- 1.1 Что такое экономико-математическая модель
- 1.2 Видео по теме:
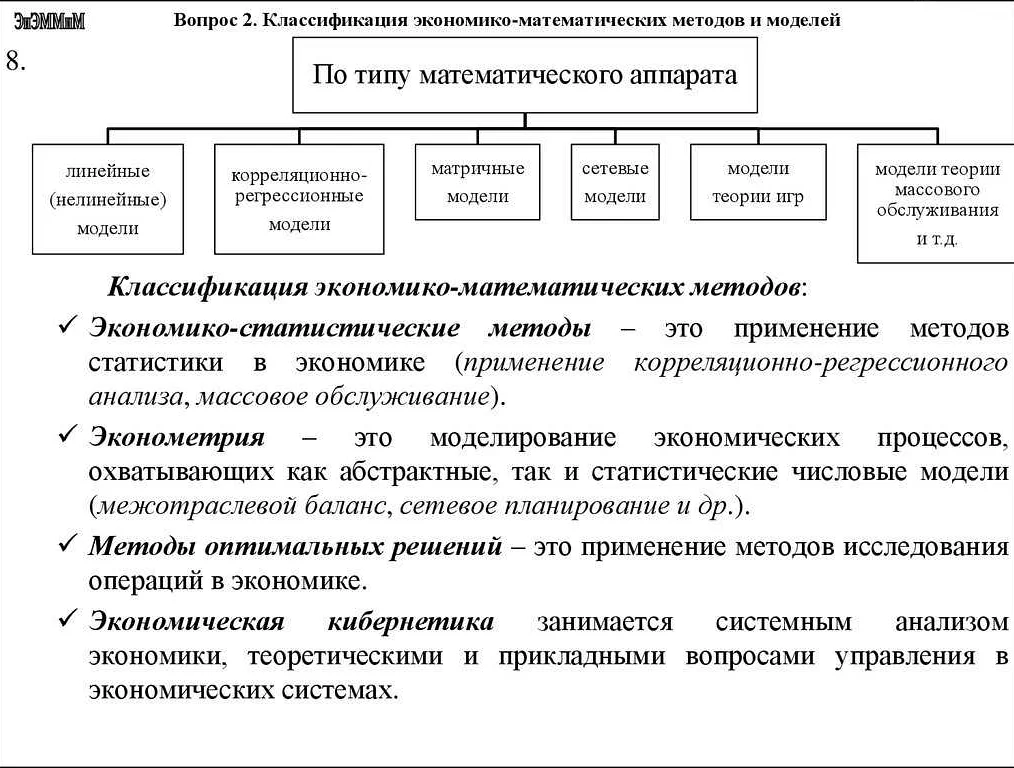
- 1.3 Классификация неизвестных в модели
- 1.4 Группа структурных неизвестных величин
- 1.5 Примеры структурных неизвестных в экономико-математической модели
- 1.6 Группа статистических неизвестных величин
- 1.7 Примеры статистических неизвестных в экономико-математической модели
- 1.8 Группа параметрических неизвестных величин
- 1.9 Примеры параметрических неизвестных в экономико-математической модели
- 1.10 Группа шумовых неизвестных величин
- 1.11 Примеры шумовых неизвестных в экономико-математической модели
- 1.12 Группа функциональных неизвестных величин
- 1.13 Примеры функциональных неизвестных в экономико-математической модели
- 1.14 Вопрос-ответ:
- 1.14.0.1 Что такое группы неизвестных величин в экономико-математической модели?
- 1.14.0.2 Какие бывают виды групп неизвестных величин?
- 1.14.0.3 Как сформулировать гипотезу о значении группы неизвестных величин?
- 1.14.0.4 Какие методы применяются для оценки групп неизвестных величин в экономико-математической модели?
- 1.14.0.5 Какие бывают примеры групп неизвестных величин в экономике?
- 1.14.0.6 Как наличие группы неизвестных величин влияет на точность прогнозов в экономической модели?
- 1.14.0.7 Какие сложности могут возникнуть при определении групп неизвестных величин в экономической модели?
Статья рассказывает о том, какие группы неизвестных величин могут быть включены в экономико-математическую модель. Вы узнаете о методах и техниках построения моделей, об их приложениях в экономике и важности математического подхода для анализа комплексных экономических процессов.
Экономико-математическая модель – это искусственное отображение реальности, в котором используются математические методы для изучения экономических взаимосвязей и принятия рациональных решений. Одним из важных элементов любой модели являются неизвестные величины, которые нужно определить для достижения нужного результата. Но иногда одну неизвестную величину невозможно определить – зато можно определить несколько их групп, которые сообщают информацию о модели.
В данной статье мы рассмотрим, какие бывают группы неизвестных величин и как их можно использовать в экономико-математических моделях. Также мы рассмотрим конкретные примеры использования группы неизвестных величин в моделях.
Группа неизвестных величин – это набор нескольких неизвестных величин, которые имеют общие свойства или связи между собой. Группы можно использовать для решения задач множественной регрессии, когда необходимо определить несколько неизвестных параметров, отвечающих за разные аспекты модели. Каждая группа может включать в себя только те параметры, которые тесно связаны между собой.
Что такое экономико-математическая модель
Экономико-математическая модель — это абстрактная математическая конструкция, которая отражает модель какой-либо реальной экономической системы. Она используется для проведения научных исследований в области экономики, финансов и управления, которые позволяют определить закономерности и взаимосвязь различных элементов этих систем.
Экономико-математическая модель может быть представлена в виде уравнений, графиков, таблиц, диаграмм и других математических форм.
Она позволяет находить оптимальные решения в сфере экономики и управления, прогнозировать поведение экономических агентов, оценивать риски и эффективность инвестиций, а также исследовать влияние различных факторов на состояние экономики и финансовой системы.
- Статическая модель — отражает состояние системы в конкретный момент времени.
- Динамическая модель — отражает изменение состояния системы со временем.
- Стохастическая модель — учитывает случайные факторы и вероятностные закономерности.
- Оптимизационная модель — находит оптимальное решение задачи при заданных условиях.
Математические модели являются неотъемлемой частью современной экономической науки и используются для решения множества экономических задач и проблем.
Видео по теме:
Классификация неизвестных в модели
В экономико-математических моделях необходимо описывать различные переменные и параметры, которые могут быть известными или неизвестными. Неизвестные величины, как правило, являются центральными объектами моделирования. Классификация неизвестных в модели имеет большое значение, поскольку определение и отображение неизвестных в модели является основой для построения модели и выявления зависимости между различными переменными.
В экономико-математических моделях существует несколько типов неизвестных величин:
- Эндогенные неизвестные — это переменные, зависимые от других переменных в модели. Они являются объектом анализа и определения. Примерами могут служить цены, объем производства, потребление, инфляция и др.
- Экзогенные неизвестные — это переменные, не зависящие от других переменных внутри модели, но которые могут влиять на переменные в модели. Примерами могут служить внешние экономические шоки, изменение налоговой или денежной политики и др.
- Параметры — это константы, которые определяют свойства системы, но они не включаются в уравнения модели. Они могут быть известными или неизвестными. Примерами могут служить коэффициенты уравнений, начальные условия и др.
Классификация неизвестных в модели является важным шагом в построении математической модели. Правильное определение типа неизвестных в модели позволяет более точно определить зависимости между переменными и лучше описать систему в целом.
Группа структурных неизвестных величин
Структурные неизвестные величины — это величины, описывающие отношения между переменными в экономико-математической модели. Группа структурных неизвестных величин, как правило, включает в себя параметры модели, коэффициенты регрессии, эластичности и другие экономические показатели.
Группа структурных неизвестных величин играет важную роль в прогнозировании экономических явлений и определении оптимальной стратегии. Например, в модели спроса и предложения структурные неизвестные величины могут включать в себя коэффициенты уравнения спроса (цены и доходы) и коэффициенты уравнения предложения (цены и затраты).
Важно отметить, что точность модели зависит от точности определения структурных неизвестных величин. По этой причине существует целый ряд методов и подходов к оценке и определению этих величин.
Примеры структурных неизвестных величинНазваниеОписание
| Коэффициент регрессии | Отражает влияние одной переменной на другую в модели регрессии |
| Эластичность спроса | Отражает изменение величины спроса на единицу изменения цены |
| Технологические коэффициенты | Отражают уровень использования ресурсов в производстве товаров и услуг |
Применение структурных неизвестных величин позволяет учитывать взаимосвязи между переменными в экономико-математической модели и, следовательно, улучшать точность прогнозирования и принимать более эффективные решения в экономической деятельности.
Примеры структурных неизвестных в экономико-математической модели
1. Технологические коэффициенты
Технологические коэффициенты – одна из основных структурных неизвестных в экономико-математических моделях. Они определяют соотношение между произведенными благами и используемыми ресурсами. Это важный параметр при оценке совокупного спроса и предложения, а также при проведении анализа чувствительности экономической модели.
2. Эластичности спроса и предложения
Эластичности спроса и предложения – это еще одна важная группа структурных неизвестных, используемых в экономико-математических моделях. Они определяют, насколько сильно изменится требуемое количество продукта при изменении цены или дохода. Эта информация необходима при формировании ценовой политики и оценке воздействия экономических изменений на рынок.
3. Функции производственной возможности
Функции производственной возможности (ФПВ) определяют максимальное количество продукта, которое может быть произведено при заданных ресурсах и технологии. ФПВ используются при создании экономико-математических моделей для предсказания результатов производства при различных условиях.
4. Спрос на труд и капитал
Спрос на труд и капитал – это структурные неизвестные, определяющие рыночные цены на труд и капитал. Эта информация важна для анализа тенденций на рынке труда и рынке капитала, а также для прогнозирования экономической активности и уровня занятости.
Группа статистических неизвестных величин
В математических моделях экономики часто возникают группы статистических неизвестных величин, которые представляют собой совокупности случайных величин, связанных между собой определенным образом. Эти статистические неизвестные величины могут быть как дискретными, так и непрерывными.
Один из примеров группы статистических неизвестных величин — это совокупность случайных величин, характеризующих поведение цен на рынке. В этом случае, каждая отдельная случайная величина является ценой на определенный товар, а группа — это множество цен на все товары, представленные на рынке.
Другой пример группы статистических неизвестных величин — это набор коррелирующих случайных величин, связанных между собой определенной зависимостью. Эта группа может быть использована при исследовании взаимосвязи между различными экономическими переменными, такими как уровень дохода и объем инвестиций в определенной сфере.
- Важно отметить, что группы статистических неизвестных величин часто используются в экономико-математических моделях для описания комплексных явлений, не имеющих однозначного объяснения или прогноза.
- Также, для анализа групп статистических неизвестных величин могут применяться различные методы статистического анализа, включая скользящие средние, регрессионный анализ и методы сглаживания данных.
Примеры статистических неизвестных в экономико-математической модели
В экономико-математических моделях неизвестными могут быть такие показатели, как:
- Средняя продолжительность жизни: Это статистический показатель, который может быть важен в моделировании систем здравоохранения, социального обеспечения и пенсионных фондов. В зависимости от возрастных и социальных групп статистическая неопределенность этой величины может повлиять на принятие важных экономических решений.
- Уровень безработицы: Данный показатель используется для оценки экономической стабильности в стране. Его использование в моделировании экономических процессов позволяет предсказать уровень экономической активности и ожидаемый спрос на товары и услуги в определенных секторах экономики.
- Объем производства: Данный параметр используется для оценки экономической активности в различных отраслях экономики и его статистическая неопределенность может влиять на моделирование экономических процессов.
Независимо от того, какие признаки будут выбраны в качестве неизвестных в экономико-математической модели, статистическая неопределенность будет оставаться одним из основных факторов, повлиять на точность прогнозирования экономических процессов.
Группа параметрических неизвестных величин
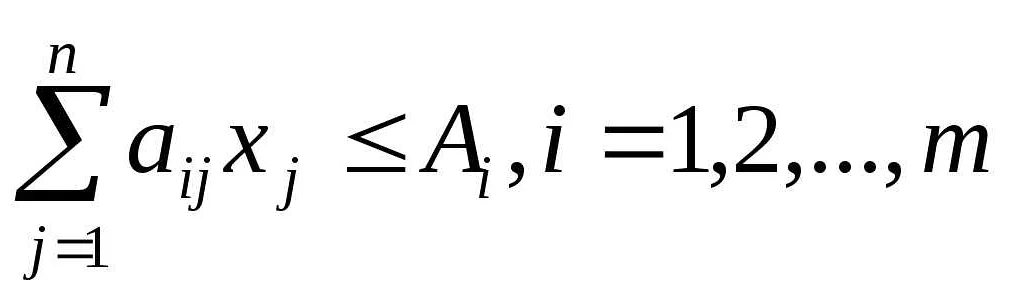
Одной из важных групп неизвестных в экономико-математических моделях являются параметрические неизвестные величины. Это значит, что данные переменные зависят от каких-то параметров, которые можно подобрать определенным образом.
К примеру, в модели спроса и предложения на рынке ценой является параметр, который влияет на количество товаров, которые будут проданы. Однако цена сама по себе может быть неизвестной величиной, поэтому она требует расчета на основе других параметров.
Другим примером параметрической неизвестной величины является кривая спроса на рынке. Эта кривая зависит от множества факторов, таких как цена, доход, предпочтения потребителей и т.д. Эти факторы, в свою очередь, могут быть параметрами, которые нужно учитывать при подборе оптимальных значений для модели.
Использование параметрических неизвестных в математических моделях является одним из способов калибровки модели для получения наиболее точных результатов. Подбирая оптимальные значения параметров, можно улучшить точность и предсказательную способность модели, что особенно важно в экономических приложениях.
Таким образом, группа параметрических неизвестных величин в экономико-математических моделях является важной компонентой, позволяющей учитывать различные факторы и получить более точные предсказания в экономических ситуациях.
Примеры параметрических неизвестных в экономико-математической модели
Параметрические неизвестные в экономико-математической модели — это неизвестные переменные, которые зависят от параметров, значения которых необходимо оценить на базе имеющихся данных. Некоторые из примеров параметрических неизвестных:
- Коэффициенты регрессии. Это пример, когда параметры не являются физическими характеристиками, но используются для определения связи между зависимой и независимой переменными. Например, в модели спроса коэффициенты регрессии могут определять, как изменится спрос на товар при изменении цены.
- Параметры распределения. В экономике и финансах используются различные распределения для описания случайных величин. Например, нормальное распределение может использоваться для описания изменений цен акций.
- Параметры симуляции. В экономических моделях используются симуляции для прогнозирования будущего поведения показателей. Параметры симуляции могут описывать различные экономические сценарии и их вероятность.
Оценка параметров в экономико-математической модели является важной задачей, поскольку точность прогнозирования зависит от точности оценки параметров. Для оценки параметров используются различные методы, такие как метод максимального правдоподобия и метод наименьших квадратов.
Группа шумовых неизвестных величин
Шумовые неизвестные величины – это такие величины, которые не поддаются точному измерению или определению. Они возникают, например, из-за погрешностей в измерительных приборах или неопределенностей в данных.
Группа шумовых неизвестных величин в экономико-математической модели является важным элементом при анализе экономических явлений. Их наличие должно быть учтено для того, чтобы добиться большей точности и надежности результатов, получаемых при решении задач.
Примеры шумовых неизвестных величин в экономике могут быть различными: это могут быть факторы, влияющие на продажи продукции (например, погода или экономические события), факторы, влияющие на уровень безработицы (демографические изменения, структура рынка труда и другие), факторы влияющие на объемы инвестиций в экономику (например, изменение процентной ставки в банках).
Для того, чтобы учесть влияние шумовых неизвестных величин на экономические процессы, необходимо использовать математические модели, которые учитывают их наличие и влияние на результаты. Такие модели позволяют улучшить прогнозирование и принятие экономических решений, а также помогают более точно оценить эффект от изменения определенных переменных.
В итоге, группа шумовых неизвестных величин является важным элементом экономико-математической модели, который должен быть учтен при анализе экономических явлений. Использование соответствующих математических методов позволяет получить более точные результаты и добиться большей надежности при принятии экономических решений.
Примеры шумовых неизвестных в экономико-математической модели
В экономико-математических моделях шумовые неизвестные являются факторами, которые могут повлиять на результаты моделирования. Например, шумовыми могут быть сезонные колебания, случайные изменения погоды или экономических показателей.
Одним из примеров шумовых факторов является шум транзакций на фондовом рынке. Шум включает в себя новости, слухи, изменения политики и другие факторы, которые могут повлиять на цены акций. Шум может быть очень сложным для прогнозирования и может создавать значительные трудности для моделей.
- Еще примером шумовой неизвестной является неопределенность во время принятия решений. Это может быть связано с выбором поставщиков, ценовой политики и другими важными решениями, которые влияют на эффективность и прибыльность бизнеса.
- В экономических моделях также могут использоваться шумы, связанные с изменениями в экономике страны. Например, это может быть связано с налоговой политикой, уровнем инфляции или величиной безработицы. Эти факторы могут значительно изменить результаты моделирования.
Шумовые неизвестные могут быть очень сложными для моделирования. Важно учитывать их в моделях, чтобы верно прогнозировать результаты. Предприятия всегда должны учитывать шумовые факторы при проведении анализа рисков и прогнозировании результатов бизнеса.
Группа функциональных неизвестных величин
Функциональные неизвестные величины представляют собой зависимости между неизвестными показателями, обрабатываемыми в экономико-математической модели. Такая группа может содержать от одного до нескольких десятков функциональных неизвестных величин.
Примерами функциональных неизвестных величин могут служить показатели, характеризующие динамику цен на продукцию или изменение доходов населения. Для определения этих показателей необходимо выявить функциональную зависимость между различными экономическими факторами, такими как уровень инфляции, налоги или уровень безработицы.
Группа функциональных неизвестных величин может быть представлена в виде математической модели, которая позволяет рассчитывать значения показателей на основе имеющихся данных. Эта модель может служить основой для прогнозирования изменений в экономической ситуации и принятия решений в сфере управления.
Для анализа группы функциональных неизвестных величин могут использоваться различные методы, включая статистические и экономические анализы. Их применение помогает выявлять зависимости между экономическими показателями и прогнозировать динамику развития отдельных секторов экономики.
Примеры функциональных неизвестных в экономико-математической модели
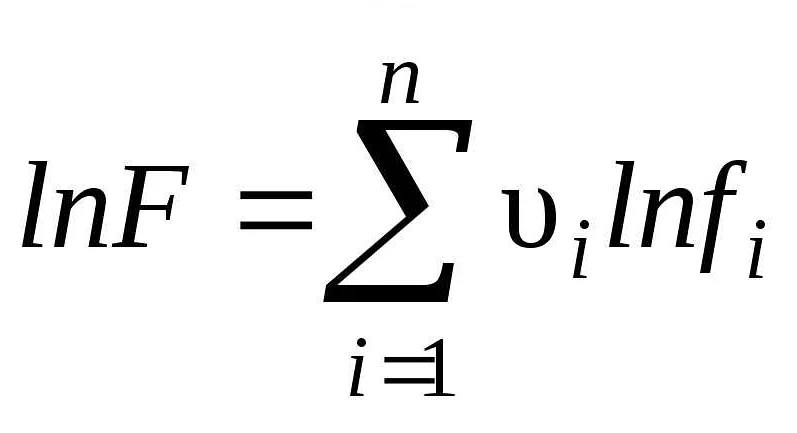
Функциональные неизвестные – это неизвестные, которые являются функциями от других переменных. В экономико-математической модели функциональные неизвестные применяются для описания зависимости между различными экономическими показателями.
Примером функциональной неизвестной является спрос на продукты. Он зависит от цены, дохода и других факторов, и может быть представлен как функция от этих переменных. Еще одним примером является производство, которое также может зависеть от цены и ресурсов.
Функциональные неизвестные могут быть представлены в виде уравнений, которые связывают их с другими переменными в модели. Например, в модели макроэкономики инфляция может быть представлена как функция от многих переменных, включая уровень безработицы, денежную массу и уровень производства.
Функциональные неизвестные могут быть использованы для описания сложных экономических систем, чтобы предсказать поведение рынка в будущем. Они могут помочь экономистам и политикам принимать более обоснованные решения по управлению экономикой.
Вопрос-ответ:
Что такое группы неизвестных величин в экономико-математической модели?
Группы неизвестных величин — это вид параметров, значений или функций, которые входят в модель экономических явлений и неизвестны на данном этапе. Их определение является ключевым в построении и оценке экономико-математических моделей и имеет большое значение при прогнозировании экономических процессов.
Какие бывают виды групп неизвестных величин?
В зависимости от характера экономической модели, группы неизвестных величин могут быть линейными, нелинейными, параметрическими и непараметрическими. Линейные группы представляют собой матрицы коэффициентов, нелинейные — функции от зависимых и независимых переменных, параметрические — модели со свободными и параметрическими коэффициентами, непараметрические — модели, обучаемые методами машинного обучения.
Как сформулировать гипотезу о значении группы неизвестных величин?
Гипотеза обычно формулируется как утверждение о статистической связи между группой неизвестных величин и другими переменными из модели. Ее задача состоит в проверке статистической значимости данной группы на базе экономических данных. Для этого используются методы статистического анализа, такие как t-тест, F-тест и др.
Какие методы применяются для оценки групп неизвестных величин в экономико-математической модели?
Для оценки групп неизвестных величин используются методы максимального правдоподобия, МНК (метод наименьших квадратов), методы стохастического программирования и др. Метод максимального правдоподобия — это метод, при котором оценки параметров модели выбираются таким образом, чтобы вероятность, с которой наблюдаемые данные могут быть получены на выбранной модели, была максимальной. МНК — метод, при котором значения параметров модели минимизируют сумму квадратичных ошибок между наблюдаемыми значениями и прогнозами модели.
Какие бывают примеры групп неизвестных величин в экономике?
Примерами групп неизвестных величин могут быть биржевые котировки, производственные объемы, валютные курсы, изменение цен на товары и услуги, темпы экономического роста и др. В свою очередь, для оценки групп неизвестных величин могут быть использованы различные математические модели, такие как модели насыщения, регрессионные модели, анализ временных рядов и др.
Как наличие группы неизвестных величин влияет на точность прогнозов в экономической модели?
Чем больше групп неизвестных величин входит в экономическую модель, тем меньше точность ее прогнозов, так как имеется большее количество неизвестных параметров. Точность прогнозов также зависит от выбранной методологии оценки групп неизвестных величин и использования различных методов статистического анализа. Однако наличие групп неизвестных величин является необходимым условием для создания более точных экономико-математических моделей.
Какие сложности могут возникнуть при определении групп неизвестных величин в экономической модели?
Одной из сложностей является нехватка данных или недостаточность объема исследуемых данных, что может повлиять на точность результатов оценки. Также сложности могут возникнуть при выборе метода оценки групп неизвестных величин, так как различные методы могут приводить к разным результатам. Кроме того, использование неправильных переменных в модели может привести к неправильным оценкам групп неизвестных величин и, соответственно, к неточности результатов прогнозирования.