Математика как найти время скорость и расстояние

Узнайте, как использовать простые математические формулы для нахождения времени, скорости и расстояния в различных физических задачах. Откройте простые способы решения проблем, связанных с перемещением и движением.

Нахождение времени, скорости и расстояния является важной частью решения многих математических задач. Эти концепции имеют применение в различных областях, включая физику, экономику и геометрию. Понимание методов и формул, используемых для нахождения времени, скорости и расстояния, поможет вам решить сложные задачи и улучшить свои математические навыки.

Для начала, давайте определим основные понятия. Время отражает продолжительность события или процесса. Оно измеряется в секундах, минутах, часах и т. д. Скорость определяет, как быстро объект перемещается. Её обычно измеряют в метрах в секунду, километрах в час и так далее. Расстояние представляет собой протяженность между двумя точками и измеряется в метрах, километрах, милях и других единицах измерения.

Существует несколько формул, которые помогут вам рассчитать время, скорость и расстояние. Одна из самых простых формул — это формула времени, в которой время равно расстоянию, деленному на скорость. Другая формула позволяет рассчитать скорость, зная расстояние и время. И наконец, можно найти расстояние, зная время и скорость. В этом руководстве мы подробно рассмотрим каждую из этих формул и покажем, как применять их в различных задачах.

Значение изучения времени, скорости и расстояния в математике

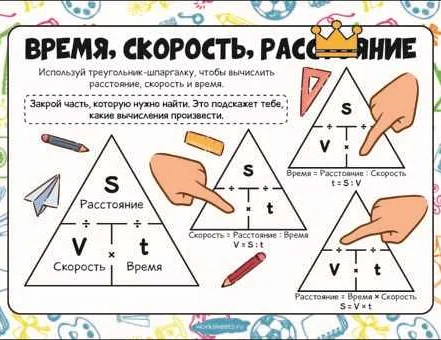
Изучение времени, скорости и расстояния имеет ключевое значение в математике и практическом применении этих понятий. Эти концепции позволяют нам измерять и описывать движение объектов, а также рассчитывать время, необходимое для достижения определенного расстояния с определенной скоростью.

Знание времени, скорости и расстояния важно не только для физики и инженерии, но и для других областей жизни. Например, в автомобильной промышленности, знание скорости и расстояния позволяет рассчитать время, за которое автомобиль достигнет пункта назначения, а также расход топлива на этом пути.

Изучение времени, скорости и расстояния также помогает развивать логическое мышление и аналитические навыки. При решении задач на эти темы необходимо анализировать информацию, проводить вычисления и делать логические выводы. Эти умения также могут быть полезны в других областях, требующих аналитического мышления, например, в экономике или программировании.

Изучение времени, скорости и расстояния также может помочь развить практические навыки. Подсчет времени, скорости и расстояния в реальных ситуациях, таких как путешествия или спортивные соревнования, помогает развить навыки планирования и оценки. Кроме того, эти концепции могут быть применены для решения повседневных задач, таких как покупка билетов на поезд или определение оптимального маршрута.

Таким образом, изучение времени, скорости и расстояния в математике имеет важное значение не только для научных и технических областей, но и для развития логического мышления, аналитических навыков и практических умений. Понимание этих концепций позволяет нам более точно измерять и описывать движение объектов в реальном мире и применять эти знания в различных сферах жизни.

Раздел 1: Основные понятия

1. Время — это величина, которая измеряет длительность происшествия или события. Обозначается буквой «t» и измеряется в секундах, минутах, часах и т.д. Время может быть измерено как в абсолютных значениях (например, 10 секунд), так и в относительных значениях (например, 2 часа больше, чем 3 часа назад).

2. Скорость — это величина, которая измеряет, насколько быстро объект перемещается относительно другого объекта или точки отсчета. Обозначается буквой «v» и измеряется в метрах в секунду, километрах в час и т.д. Скорость может быть постоянной (когда объект движется с постоянной скоростью), а также переменной (когда скорость изменяется со временем).

3. Расстояние — это величина, которая измеряет протяженность между двумя объектами или точками. Обозначается буквой «d» и измеряется в метрах, километрах и т.д. Расстояние может быть вычислено как длина прямой линии между двумя точками, а также как сумма протяженностей всех отрезков пути с учетом направления движения.

В этом разделе мы рассмотрели основные понятия времени, скорости и расстояния, которые играют важную роль в математике. Понимание этих понятий поможет нам в дальнейшем решении задач и применении соответствующих математических формул.

Что такое время в математике

Время в математике обычно измеряется в единицах, таких как секунды, минуты, часы или дни. Эти единицы измерения позволяют нам определить продолжительность событий или изменения величин, таких как расстояние или скорость.

Время также может быть представлено в виде числа или точки на числовой оси. Например, если мы хотим измерить время, прошедшее с начала дня, мы можем представить его в виде числа от 0 до 24 часов. Точка на числовой оси будет соответствовать определенному моменту во времени.

В математике время также может быть представлено в виде промежутков, таких как интервалы или отрезки времени. Это позволяет нам измерять разницу между двумя моментами времени или определить длительность события.

Время в математике является важным понятием при решении задач, связанных с расчетом скорости и расстояния. Знание времени позволяет нам определить, как долго займет пройти определенное расстояние с определенной скоростью или наоборот, определить скорость, зная расстояние и время.

Таким образом, понимание времени в математике является фундаментальным для решения различных задач и является неотъемлемой частью изучения математики.

Понятие скорости в математике

Величина скорости измеряется в единицах расстояния, например, километрах или метрах, деленных на единицу времени, например, часы или секунды. Обычно скорость измеряется в километрах в час (км/ч) или в метрах в секунду (м/с).

Скорость может быть выражена как средняя скорость или мгновенная скорость. Средняя скорость рассчитывается как отношение общего расстояния, пройденного в течение определенного времени, к этому времени. Мгновенная скорость, с другой стороны, является скоростью в конкретный момент времени и может быть найдена с помощью предельного значения.

В математике скорость также может быть представлена в виде графика, изображающего зависимость пройденного расстояния от времени. Это называется скоростной график и позволяет наглядно представить, как скорость меняется в течение времени.

Знание понятия скорости в математике полезно для решения различных задач, связанных с движением и изменением позиции в пространстве. Оно также может быть использовано для моделирования и предсказания различных процессов, таких как транспортное движение, движение планет и других физических явлений.

Расстояние: определение и значение

Расстояние может быть измерено в различных единицах, таких как метры, километры, мили и другие. Это зависит от контекста и способа измерения. Например, для измерения расстояния между двумя городами можно использовать километры, а для измерения длины комнаты — метры.

Расстояние также имеет значение в физике, где оно играет важную роль в определении скорости и времени. Например, для расчета скорости движения объекта необходимо знать расстояние, которое он преодолел за определенное время.

В математике расстояние может быть вычислено с использованием различных формул и методов. Например, для вычисления расстояния между двумя точками на плоскости можно использовать теорему Пифагора или формулу расстояния между двумя точками.

Понимание расстояния и его значение является неотъемлемой частью математики, физики и других наук. Оно позволяет измерять и анализировать пространство, движение и взаимодействие объектов, что является важным для понимания окружающего мира.

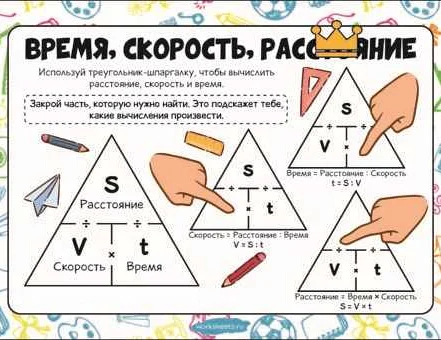
Раздел 2: Формулы для вычисления времени, скорости и расстояния

В математике существуют определенные формулы, которые позволяют вычислить время, скорость и расстояние в различных ситуациях. Знание этих формул может быть полезно при решении задач и проведении различных вычислений.

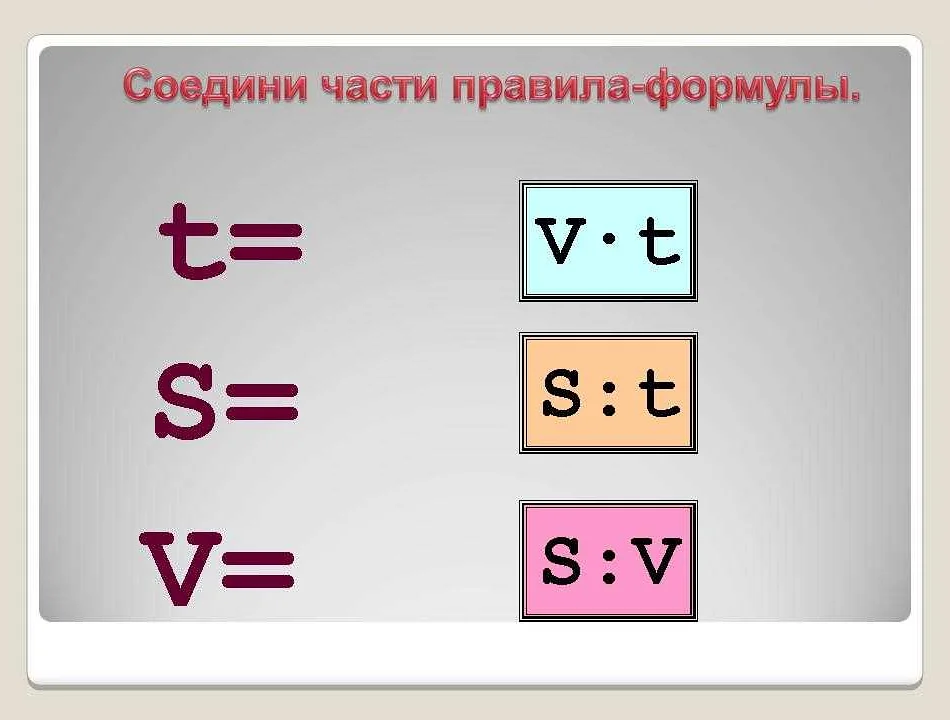
Время (t), скорость (v) и расстояние (d) связаны между собой следующим образом:

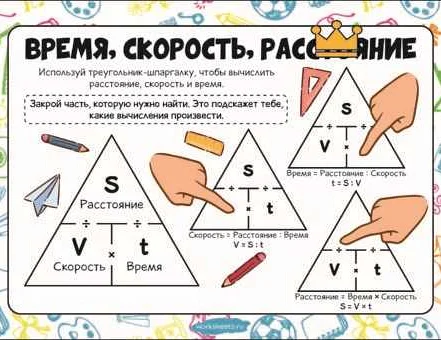
• Если известна скорость и время, можно вычислить расстояние по формуле: d = v * t.
• Если известны скорость и расстояние, можно вычислить время по формуле: t = d / v.
• Если известны время и расстояние, можно вычислить скорость по формуле: v = d / t.

Эти формулы основаны на простом математическом соотношении: скорость равна отношению расстояния к времени. Для решения задач, связанных с вычислением времени, скорости и расстояния, необходимо знать две из трех величин и использовать соответствующую формулу для вычисления третьей.

Например, если известна скорость автомобиля (60 км/ч) и время его движения (3 часа), можно вычислить расстояние, которое проехал автомобиль: d = 60 * 3 = 180 км.

Важно помнить, что величины времени, скорости и расстояния должны быть измерены в одних и тех же единицах, чтобы формулы были применимы. Например, если скорость измеряется в километрах в час, то и время должно быть измерено в часах, а расстояние — в километрах.

Использование этих формул позволяет с легкостью решать задачи, связанные с вычислением времени, скорости и расстояния, и найти неизвестную величину при известных двух других.

Формула времени в зависимости от скорости и расстояния

Формула времени в математике позволяет найти время, зная скорость и расстояние. Она основана на пропорциональной зависимости между этими тремя величинами. Формула выглядит следующим образом:

Время = Расстояние / Скорость

В этой формуле, Время обозначает время пути, то есть время, за которое объект или человек проходит определенное расстояние. Расстояние указывается в единицах измерения длины, например, в метрах или километрах. Скорость указывается в единицах измерения длины за единицу времени, например, метрах в секунду или километрах в час.

Для использования этой формулы, необходимо знать две из трех величин: время, скорость или расстояние. Если известны время и скорость, можно найти расстояние, умножив время на скорость и получив результат в единицах измерения длины. Если известны время и расстояние, можно найти скорость, разделив расстояние на время и получив результат в единицах измерения длины за единицу времени.

Формула времени в зависимости от скорости и расстояния является одной из основных формул в физике и математике, и она часто применяется для решения задач, связанных с перемещением объектов или людей.

Важно помнить, что величины должны быть измерены в одних и тех же единицах измерения для получения корректного результата. Также следует учесть, что формула работает только в случае постоянной скорости.

Как определить скорость, зная время и расстояние

Для определения скорости, зная время и расстояние, необходимо воспользоваться формулой:

Скорость = Расстояние / Время

Данная формула позволяет вычислить скорость, если известны величины времени и расстояния. Для этого необходимо разделить значение расстояния на значение времени.

Например, если известно, что расстояние равно 100 метров, а время равно 10 секунд, то можно определить скорость следующим образом:

Скорость = 100 м / 10 с = 10 м/с

Таким образом, скорость равна 10 метров в секунду. Это означает, что объект проходит 10 метров за одну секунду.

Зная время и расстояние, можно определить скорость, что является важной задачей в физике и многих других науках. Знание формулы и умение ее применять позволяет решать различные задачи, связанные с движением и скоростью.

Формула расстояния при известной скорости и времени

В математике существует формула, позволяющая вычислить расстояние, пройденное объектом, если известны его скорость и время движения.

Формула имеет следующий вид:

Расстояние = Скорость × Время

Где:

• Расстояние — пройденное объектом расстояние;
• Скорость — скорость движения объекта;
• Время — время движения объекта.

Для использования этой формулы необходимо знать значения скорости и времени. Если значения известны, их нужно подставить в формулу, чтобы получить искомое расстояние.

Например, если объект движется со скоростью 50 км/ч в течение 2 часов, можно вычислить расстояние по формуле:

Расстояние = 50 км/ч × 2 ч = 100 км

Таким образом, объект пройдет расстояние 100 км за 2 часа при скорости 50 км/ч.

Вопрос-ответ:

Как найти время, скорость и расстояние при известных двух параметрах?

Если известны два параметра, то третий можно вычислить с помощью соответствующей формулы. Например, для вычисления времени используйте формулу t = s/v, где s — расстояние, v — скорость. Аналогично, для вычисления скорости используйте формулу v = s/t, и для вычисления расстояния используйте формулу s = v * t.

Как найти скорость, если известны расстояние и время?

Для вычисления скорости при известных расстоянии и времени используйте формулу v = s/t, где v — скорость, s — расстояние, t — время.

Как найти расстояние, если известны скорость и время?

Для вычисления расстояния при известной скорости и времени используйте формулу s = v * t, где s — расстояние, v — скорость, t — время.

Как найти время, если известны скорость и расстояние?

Для вычисления времени при известной скорости и расстоянии используйте формулу t = s/v, где t — время, s — расстояние, v — скорость.

Можно ли использовать эти формулы для вычисления времени, скорости и расстояния в разных единицах измерения?

Да, можно использовать эти формулы для вычисления времени, скорости и расстояния в разных единицах измерения. Главное, чтобы все величины были выражены в одинаковых единицах. Например, если расстояние измерено в километрах, то и скорость должна быть выражена в километрах в час, чтобы получить время в часах.

Как найти время, скорость и расстояние в математике?

Для того чтобы найти время, скорость и расстояние в математике, вы можете воспользоваться формулой V = S / t, где V — скорость, S — расстояние и t — время. Если у вас есть два известных значения, вы можете использовать эту формулу для нахождения третьего.

Раздел 3: Практическое применение понятий времени, скорости и расстояния

Понимание понятий времени, скорости и расстояния имеет огромное практическое применение в различных областях жизни, начиная от физики и математики и заканчивая повседневными задачами.

Один из основных способов применения этих понятий — определение времени, необходимого для преодоления расстояния с определенной скоростью. Например, если автомобиль движется со скоростью 60 км/ч и необходимо проехать расстояние в 240 км, можно легко определить время, которое потребуется для этого. Для этого необходимо разделить расстояние на скорость: 240 км / 60 км/ч = 4 часа. Таким образом, автомобилю потребуется 4 часа, чтобы преодолеть указанное расстояние.

Другим примером практического применения понятий времени, скорости и расстояния является определение скорости, исходя из известного расстояния и времени. Например, если автомобиль проехал расстояние в 120 км за 2 часа, можно легко определить скорость, с которой он двигался. Для этого необходимо разделить расстояние на время: 120 км / 2 часа = 60 км/ч. Таким образом, скорость автомобиля составляла 60 км/ч.

Знание этих понятий также может быть полезно при решении задач о телах, движущихся с постоянной скоростью. Например, можно определить расстояние, которое пройдет тело за определенное время с известной скоростью, умножив скорость на время. Например, если автомобиль движется со скоростью 50 км/ч и движется в течение 3 часов, расстояние, которое он пройдет, будет равно 50 км/ч * 3 часа = 150 км.

Все эти примеры демонстрируют практическое применение понятий времени, скорости и расстояния в различных сферах нашей жизни. Знание этих понятий позволяет решать различные задачи эффективно и уверенно.

Видео по теме: