Что такое медиана в математике

Медиана в математике — это значение, которое разделяет упорядоченную выборку на две равные части. Она является одним из параметров центральной тенденции и часто используется для измерения типичного значения в статистическом анализе данных.

Медиана — это одна из основных характеристик набора чисел или статистической выборки. Она является центральным значением, разделяющим набор на две равные части. Другими словами, медиана показывает значение, которое находится посередине, когда все числа упорядочены по возрастанию или убыванию.

Для вычисления медианы необходимо отсортировать набор чисел и выбрать значение, которое находится посередине. Если набор содержит нечетное количество чисел, медиана будет равна значению, которое находится точно посередине. Если же количество чисел четное, медиана вычисляется как среднее арифметическое двух значений, которые находятся посередине набора.

Пример: рассмотрим набор чисел {2, 4, 6, 8, 10}. После сортировки получим {2, 4, 6, 8, 10}. Так как количество чисел нечетное, медианой будет значение, которое находится посередине, то есть 6.

Медиана используется в различных областях, включая статистику, экономику, биологию и другие науки. Ее преимущество заключается в том, что она не так сильно подвержена влиянию выбросов, как, например, среднее арифметическое.

Что такое медиана в математике?

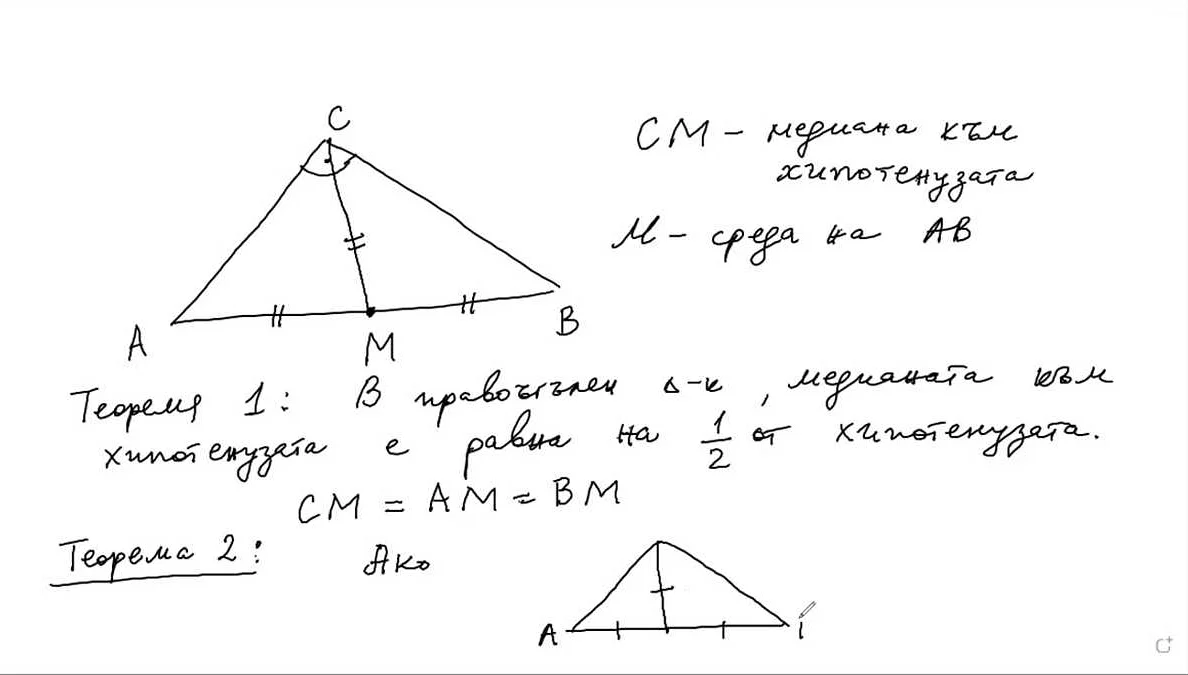
Медиана является таким значением, которое делит упорядоченный набор данных на две равные части. Другими словами, это такое число, при котором ровно половина значений находится выше, а другая половина — ниже.

Для вычисления медианы необходимо сначала упорядочить данные по возрастанию или убыванию, а затем определить значение, находящееся посередине. Если количество данных четное, то медиана определяется как среднее арифметическое двух соседних значений.

Медиана имеет несколько преимуществ перед средним арифметическим значением (средним): она более устойчива к выбросам и позволяет получить более репрезентативную оценку центральной тенденции данных в случае, когда распределение значений сильно искажено.

Примеры использования медианы в математике включают определение среднего возраста группы людей, вычисление медианного дохода в определенном регионе и анализ роста деревьев в лесу.

Как определить медиану?

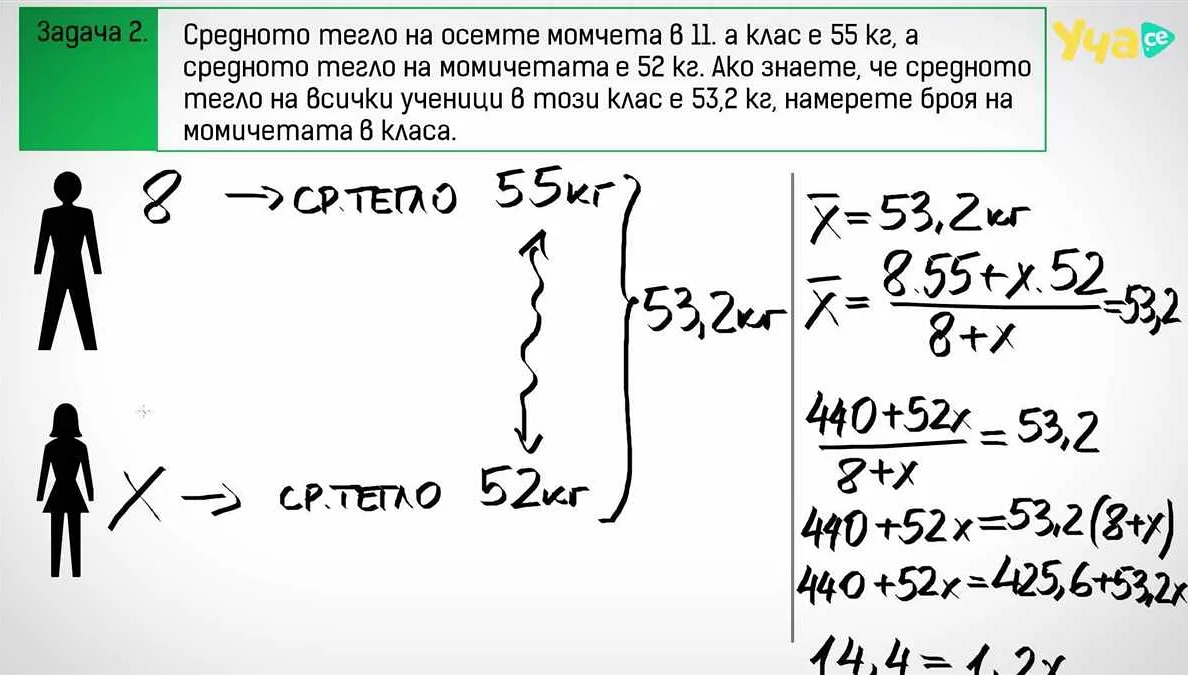
Для определения медианы в первую очередь необходимо упорядочить выборку по возрастанию или убыванию значений. Если в выборке имеется нечетное количество элементов, то медианой является значение, находящееся в середине. Если же количество элементов четное, то медиана определяется как среднее арифметическое двух соседних значений в середине выборки.

Давайте рассмотрим пример. Пусть у нас есть выборка чисел: 2, 4, 6, 8, 10. Сначала упорядочим ее по возрастанию: 2, 4, 6, 8, 10. Количество элементов в выборке равно 5, поэтому медианой будет значение, находящееся в середине, то есть 6.

Если у нас выборка чисел 1, 3, 5, 7, 9, 11, то сначала упорядочим ее по возрастанию: 1, 3, 5, 7, 9, 11. Количество элементов в выборке равно 6, поэтому медианой будет среднее арифметическое двух соседних значений в середине: (5 + 7) / 2 = 6.

Таким образом, для определения медианы необходимо упорядочить выборку и использовать указанные выше правила в зависимости от четности или нечетности количества элементов в выборке.

Примеры использования медианы в математике

1. Оценка среднего значения

Медиана может использоваться для оценки среднего значения в случае, когда имеются выбросы или аномальные значения в данных. В отличие от среднего значения, которое может быть сильно искажено выбросами, медиана является более устойчивой мерой центральной тенденции.

2. Анализ распределения

Медиана также может быть использована для анализа распределения данных. Если медиана существенно отличается от среднего значения, это может указывать на наличие скошенности в данных. Если медиана находится ближе к первому или третьему квартилю, это может указывать на симметричное или нормальное распределение данных.

3. Определение центрального значения

Медиана также может быть использована для определения центрального значения в упорядоченном ряду чисел. Например, при анализе данных о доходах населения, медиана позволяет определить, какой процент населения имеет доход ниже или выше определенного значения. Это может быть полезно при изучении неравенства в распределении доходов.

Таким образом, медиана является мощным инструментом анализа данных в математике и статистике. Она позволяет оценивать среднее значение, анализировать распределение и определять центральное значение в данных.

Формула для расчета медианы

Если у нас имеется упорядоченный набор данных с нечетным количеством элементов, то медиана находится как значение в середине набора. Например, для набора данных {1, 2, 3, 4, 5} медиана будет равна 3.

В случае, когда количество элементов в наборе данных является четным, медиана находится как среднее арифметическое двух значений в середине набора. Например, для набора данных {1, 2, 3, 4, 5, 6} медиана будет равна (3 + 4) / 2 = 3.5.

Формула для расчета медианы позволяет быстро и точно определить центральное значение в упорядоченном наборе данных.

Медиана и среднее значение: в чем разница?

Медиана — это значение, которое делит упорядоченный набор данных на две равные половины. Другими словами, половина значений будет меньше медианы, а другая половина — больше. Если набор данных содержит нечетное количество элементов, медиана будет являться средним значением. Например, в наборе данных {1, 2, 3, 4, 5} медиана равна 3.

Среднее значение — это сумма всех значений, поделенная на их общее количество. Оно вычисляется путем сложения всех значений и деления на количество элементов. Например, для набора данных {1, 2, 3, 4, 5} среднее значение равно (1 + 2 + 3 + 4 + 5) / 5 = 3.

Главное отличие между медианой и средним значением заключается в том, что медиана устойчива к выбросам и экстремальным значениям, в то время как среднее значение сильно зависит от них. Если в наборе данных есть выбросы или экстремальные значения, среднее значение будет сильно искажено и не будет отражать типичное значение. Например, если в наборе данных {1, 2, 3, 4, 100} среднее значение равно (1 + 2 + 3 + 4 + 100) / 5 = 22, медиана будет по-прежнему равна 3.

Оба показателя имеют свои преимущества и недостатки и могут быть использованы в различных ситуациях. Выбор между медианой и средним значением зависит от характера данных и целей исследования.

Границы использования медианы

Медиана имеет свои особенности и границы использования, которые следует учитывать при анализе данных:

1. Медиана может быть использована для описания распределения данных только в том случае, если значения измерений являются количественными и упорядочены. Например, медиана может быть вычислена для времени реакции, возраста, дохода и других числовых данных.

2. Медиана не зависит от выбросов. В отличие от среднего арифметического, медиана не сильно изменяется при наличии выбросов или аномальных значений. Это делает ее предпочтительным показателем центральной тенденции в случае наличия выбросов в данных.

3. Медиана не подходит для описания распределения данных в случае, если имеются значительные различия в весе или значимости различных значений. Например, при анализе доходов населения, медиана может не отразить реальное положение дел, если не учесть разницу в доходах между бедным и богатым населением.

4. Медиана является непараметрическим показателем статистики, что означает, что она не требует предположений о распределении данных. В отличие от среднего значения, медиана может быть вычислена для данных любого типа распределения.

В целом, медиана является полезным инструментом для анализа данных и описания их центральной тенденции. Ее использование позволяет учитывать особенности данных и получать более надежные результаты при анализе числовых значений.

Преимущества использования медианы

2. Адекватное отображение центрального значения: Медиана является более надежной мерой центральной тенденции, чем среднее арифметическое, особенно в случаях, когда данные имеют асимметричное распределение. Она позволяет более точно отразить типичное значение в выборке.

3. Полезность в анализе категориальных данных: Медиана может быть использована для анализа категориальных данных, таких как ранги или порядковые значения. В отличие от среднего значения, медиана может быть вычислена для таких данных и предоставить информацию о центральной тенденции.

4. Простота интерпретации: Медиана легко интерпретируется. Она представляет значение, которое разделяет выборку на две равные части. Например, медиана зарплаты в группе сотрудников показывает, что половина сотрудников получает больше этого значения, а другая половина — меньше.

5. Удобство использования при отсутствии данных: Медиана может быть вычислена, даже если в выборке присутствуют пропущенные данные или выборка имеет неравное количество значений. В отличие от среднего значения, медиана не требует полной выборки для вычисления.

6. Сохранение порядка данных: Медиана сохраняет порядок данных в выборке. Это означает, что если данные упорядочены по возрастанию или убыванию, медиана будет соответствовать позиции в этом порядке. Это полезно при анализе временных рядов или других упорядоченных данных.

Видео по теме:

Что такое медиана в математике?

Медиана в математике — это значение, которое разделяет упорядоченный набор чисел на две равные части. То есть, половина чисел из набора меньше медианы, а другая половина больше медианы.

Как найти медиану в упорядоченном наборе чисел?

Для нахождения медианы в упорядоченном наборе чисел нужно выбрать среднее значение. Если в наборе чисел нечетное количество, то медианой будет среднее число. Если же количество чисел четное, то медианой будет среднее арифметическое двух ближайших чисел к середине набора.

Как найти медиану в неупорядоченном наборе чисел?

Для нахождения медианы в неупорядоченном наборе чисел нужно сначала упорядочить его по возрастанию или убыванию. Затем можно применить ту же самую формулу, что и для упорядоченного набора чисел, чтобы найти медиану.

Как использовать медиану в статистике?

Медиана является одним из показателей центральной тенденции в статистике. Она позволяет определить среднюю величину из набора данных, исключая выбросы или экстремально большие или маленькие значения. Медиана также устойчива к асимметричным распределениям и может быть использована для сравнения различных групп или наборов данных.

Может ли медиана быть равной нулю?

Да, медиана может быть равной нулю, если в наборе данных есть ноль или если половина чисел из набора равна нулю. Но это зависит от конкретного набора чисел и его распределения.

Что такое медиана?

Медиана — это значение, которое разделяет упорядоченный набор чисел на две равные части. Если у нас есть нечетное количество чисел, то медиана — это значение, стоящее посередине. Если же у нас четное количество чисел, то медиана — это среднее арифметическое двух значений, стоящих в середине.