Угол в математике как обозначается

Угол в математике обозначается специальными символами, такими как латинская буква

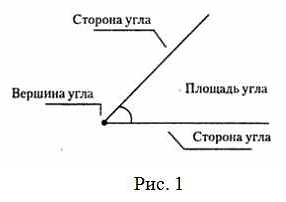
Угол — это геометрическая фигура, которая образуется двумя лучами с общим началом, называемым вершиной. В математике угол обозначается специальными символами и обладает своими свойствами и характеристиками.

Обычно угол обозначается тремя точками: вершиной и двумя точками на лучах, которые называются концами угла. Важно отметить, что порядок точек имеет значение — первая точка указывает на вершину, а две последующие точки определяют направление и размер угла.

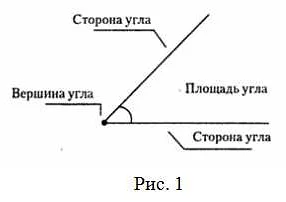
Существует несколько способов обозначить угол в математике. Один из самых распространенных способов — использование символа «∠» (знак угла), который ставится перед вершиной угла. Например, ∠ABC.

Также углы могут быть обозначены буквами. Часто для обозначения углов используются заглавные буквы латинского алфавита, причем буква, обозначающая вершину угла, ставится в середине, а две другие буквы — на концах лучей. Например, угол между лучами AB и AC может быть обозначен как ∠BAC или ∠CAB.

Углы могут быть измерены в градусах, радианах или градах. Градусы — это наиболее распространенная система измерения углов. Один полный оборот составляет 360 градусов, а каждый градус делится на 60 минут и каждая минута — на 60 секунд. Радианы — это другая система измерения углов, в которой один полный оборот составляет 2π радианов. Грады — это третья система измерения, в которой один полный оборот составляет 400 градов.

Как обозначается угол в математике

Угол в математике обозначается символом, который имеет несколько разновидностей. Основные обозначения углов в математике:

• Символ «∠». Это самое распространенное обозначение угла. Он используется как для вершинного угла, так и для угла между двумя прямыми.
• Три точки. Если угол образован тремя точками, то он обозначается этими точками. Например, угол образованный точками A, B и C обозначается как ∠ABC.
• Греческая буква «α», «β», «γ». В некоторых случаях углы обозначаются греческими буквами. Например, α может обозначать угол А.
• Цифровые обозначения. Угол может быть обозначен цифрами, например, 45° или 90°.

Примеры:

• ∠ABC — угол, образованный тремя точками A, B и C.
• ∠AOC — угол, образованный точками A, O и C.
• α — угол А.
• β — угол B.
• 45° — угол, равный 45 градусам.
• 90° — прямой угол, равный 90 градусам.

Обозначение углов в математике является стандартным и используется для удобства обозначения и визуализации геометрических фигур и конструкций.

Типы углов

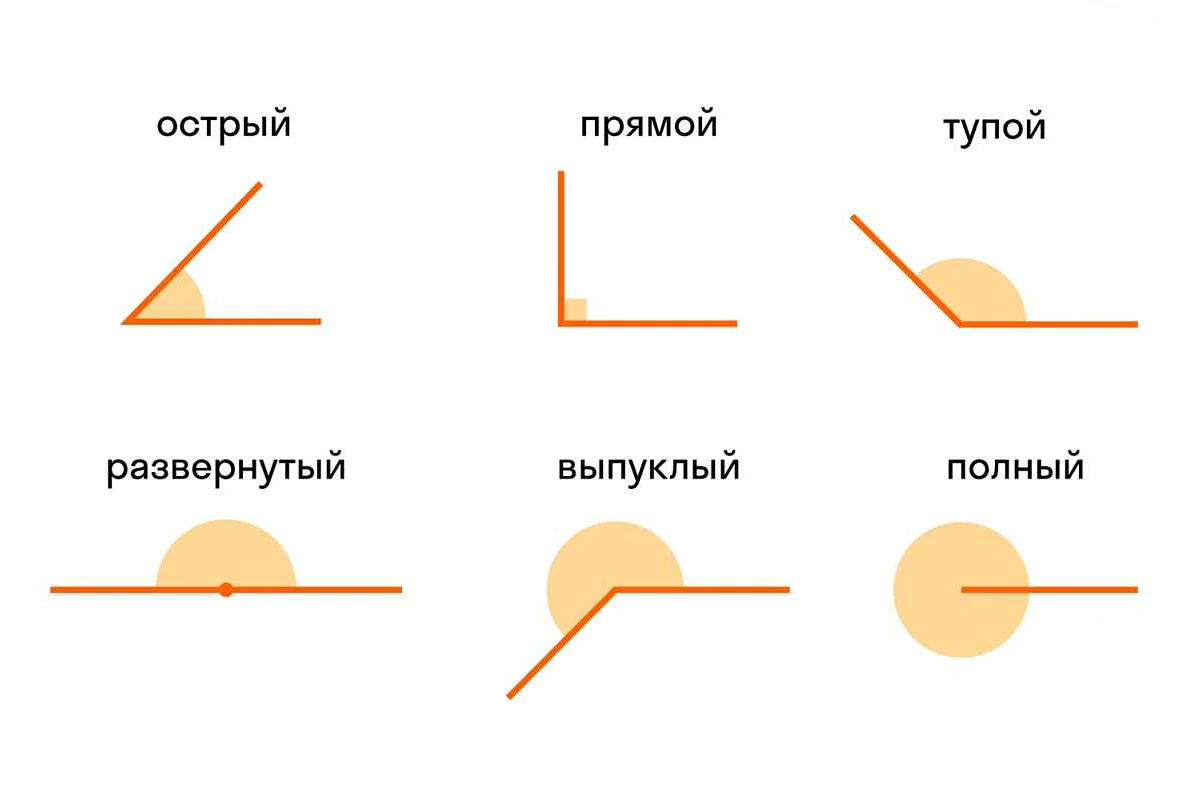
В математике существует несколько типов углов, которые можно классифицировать по различным признакам:

1. Острые углы: углы, меньшие 90 градусов. Например, угол в 30 градусов.
2. Прямые углы: углы, равные 90 градусам. Один из примеров – угол в 90 градусов.
3. Тупые углы: углы, большие 90 градусов, но меньше 180 градусов. Например, угол в 120 градусов.
4. Полные углы: углы, равные 180 градусов. Например, угол в 180 градусов.
5. Смежные углы: углы, которые имеют общую сторону и общую вершину, но не лежат на одной прямой. Например, два угла, сумма которых равна 180 градусов.
6. Вертикальные углы: углы, имеющие одинаковую меру. Например, два угла, каждый из которых равен 45 градусам.

Изучение и классификация углов является важной частью геометрии и находит применение в различных областях науки и техники.

Символы для обозначения угла

Существуют также символы, которые используются для обозначения конкретных видов углов:

• Прямой угол: обозначается символом «∟». Прямой угол равен 90 градусам или π/2 радиан.
• Острый угол: обозначается символом «⦞». Острый угол меньше 90 градусов или π/2 радиан.
• Тупой угол: обозначается символом «⦜». Тупой угол больше 90 градусов или π/2 радиан.
• Прямоугольный угол: обозначается символом «⊾». Прямоугольный угол равен 90 градусам или π/2 радиан.

Например, угол ABC можно обозначить как ∠ABC, прямой угол – как ∟ABC, острый угол – как ⦞ABC, тупой угол – как ⦜ABC, а прямоугольный угол – как ⊾ABC.

Угол в градусах

Например, прямой угол, который равен 90 градусам, обозначается как 90°. Полный оборот составляет 360 градусов, обозначается как 360°.

Угол в градусах можно измерять как в положительном, так и в отрицательном направлении. Положительное направление считается по часовой стрелке, а отрицательное — против часовой стрелки.

Также угол в градусах может быть больше 360° или отрицательным. В этом случае он считается сокращенным или многократным углом.

Угол в градусах широко используется в геометрии, физике, инженерии и других науках для измерения и описания углов и их свойств.

Угол в радианах

Для обозначения угла в радианах используется специальный символ — «рад». Угол в радианах обычно обозначается маленькой латинской буквой «α» с символом «рад» после нее, например, α рад.

Угол в радианах можно выразить через градусы по формуле: угол в радианах = (угол в градусах * π) / 180, где π (пи) — это математическая константа, приближенное значение которой равно 3.14159.

Например, если угол в градусах равен 90°, то угол в радианах можно вычислить следующим образом: угол в радианах = (90 * π) / 180 = π / 2 рад.

Угол в радианах широко используется в тригонометрии и анализе, так как позволяет более точно и удобно описывать и работать с геометрическими и тригонометрическими функциями.

Угол в градусахУгол в радианах

0°	0 рад
30°	π / 6 рад
45°	π / 4 рад
60°	π / 3 рад
90°	π / 2 рад

Примеры углов

В математике существует несколько типов углов:

Прямой угол: имеет величину 90 градусов и обозначается символом ∠.

Острый угол: имеет величину менее 90 градусов и обозначается символом ∠.

Тупой угол: имеет величину больше 90 градусов и менее 180 градусов и обозначается символом ∠.

Полный угол: имеет величину 180 градусов и обозначается символом ∠.

Например:

Угол ∠ABC равен 60 градусам и является острым углом.

Угол ∠XYZ равен 120 градусам и является тупым углом.

Угол ∠PQR равен 90 градусам и является прямым углом.

Угол ∠MNO равен 180 градусам и является полным углом.

Взаимное расположение углов

В математике углы могут находиться в различных взаимных положениях. Рассмотрим основные случаи:

• Смежные углы: два угла, которые имеют общую сторону и общую вершину. Сумма смежных углов равна 180 градусам.
• Вертикальные углы: два угла, которые находятся по разные стороны пересекающихся прямых и имеют равные меры. Сумма вертикальных углов также равна 180 градусам.
• Равные углы: два угла, которые имеют одинаковую меру.
• Дополнительные углы: два угла, сумма которых равна 90 градусам.
• Смежные дополнительные углы: два угла, которые являются смежными и вместе образуют прямой угол (180 градусов).
• Вертикально дополнительные углы: два угла, которые являются вертикальными и их сумма равна 180 градусам.

Изучение взаимного расположения углов является важной частью геометрии и позволяет решать различные задачи на нахождение неизвестных углов и сторон.

Вопрос-ответ:

Какие символы используются для обозначения углов в математике?

В математике углы обозначают с помощью трех букв или одной буквы с добавлением символа. Например, ABC, ∠A, ∠BAC.

Какие виды углов существуют в математике?

В математике существуют различные виды углов: прямой угол (90 градусов), острый угол (меньше 90 градусов), тупой угол (больше 90 градусов), прямоугольный угол (имеет 90 градусов), выпуклый угол (меньше 180 градусов), вогнутый угол (больше 180 градусов).

Как определить угол по его величине?

Угол можно определить по его величине с помощью градусов или радианов. Градусы обозначаются символом °, а радианы – символом рад.

Какие примеры углов можно привести?

Примерами углов могут служить угол в 90 градусов (прямой угол), угол в 45 градусов (острый угол), угол в 120 градусов (тупой угол).

Какие основные свойства углов существуют?

Основные свойства углов включают: сумма углов треугольника равна 180 градусов, углы на параллельных прямых равны, вертикальные углы равны, смежные углы дополняют друг друга.

Как обозначается угол в математике?

Угол в математике обозначается символом α или А.

Видео по теме: