Соотношение в математике как решать

Узнайте, как решать задачи на нахождение соотношений в математике с помощью правил и методов. Изучите примеры и шаги, которые помогут вам понять и применить соотношения в различных областях математики.

В математике соотношения играют важную роль, так как они помогают нам понять и описать взаимосвязи между различными величинами. Решение задач по соотношению требует определенных навыков и методов, которые мы рассмотрим в данной статье.

Один из основных методов решения задач по соотношению — это составление уравнений. Для этого необходимо анализировать условие задачи и выражать величины, которые неизвестны, через известные величины. Затем составляются уравнения, в которых неизвестная величина обозначается буквой, а известные величины подставляются из условия задачи. Решив полученные уравнения, можно найти значение неизвестной величины.

Например, рассмотрим задачу: «Вася и Петя вместе заработали 250 рублей. Вася заработал в 2,5 раза больше, чем Петя. Сколько рублей заработал каждый из них?»

В данной задаче мы знаем, что сумма заработка Васи и Пети составляет 250 рублей. Пусть заработок Пети будет обозначен буквой «х», тогда заработок Васи будет равен 2,5 * «х». Составим уравнение: «х + 2,5 * х = 250». Решив это уравнение, мы найдем, что Петя заработал 100 рублей, а Вася — 150 рублей.

Кроме составления уравнений, существуют и другие методы решения задач по соотношению, такие как пропорции и доли. Пропорции используются, когда нужно определить соотношение двух величин, например, при решении задач на сопротивление или скорость. Доли используются, когда нужно разделить какую-то величину на несколько частей.

В данной статье мы рассмотрим основные методы решения задач по соотношению на примерах. Надеемся, что эта информация поможет вам разобраться с такого типа задачами и успешно решить их.

Изучение соотношений в математике

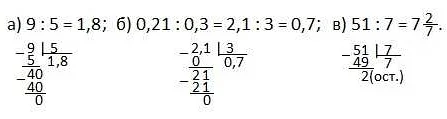
Один из основных методов решения задач по соотношению – это использование пропорций. Пропорция – это выражение, устанавливающее равенство двух отношений. Для решения задач с пропорциями необходимо найти неизвестную величину, используя уже известные соотношения.

Другим методом решения задач по соотношению является использование уравнений. Уравнение – это математическое выражение, в котором присутствуют неизвестные величины и знаки равенства. Решение уравнения осуществляется путем нахождения значений неизвестных величин, удовлетворяющих заданному условию.

При изучении соотношений в математике, важно уметь анализировать и интерпретировать информацию, представленную в виде графиков, таблиц и диаграмм. Графики и диаграммы позволяют наглядно представить зависимости и соотношения между величинами.

Изучение соотношений в математике помогает развить логическое мышление, аналитические навыки и умение решать задачи. Эти навыки являются важными не только в математике, но и в других областях науки и практической деятельности.

Понимание и использование соотношений в математике позволяет решать разнообразные задачи, связанные с пропорциональным изменением величин, расчетом процентов, вычислением средних значений и многими другими. Основные методы решения задач по соотношению, такие как использование пропорций и уравнений, помогают рационально подходить к решению задач и получать точные и надежные результаты.

Видео по теме:

Определение и основные понятия

Соотношение в математике представляет собой утверждение или связь между двумя или более величинами. В задачах по соотношению ищется значение неизвестной величины на основе известных данных и условий задачи.

Основными понятиями в задачах по соотношению являются:

Известные величины: это значения, которые даны в условии задачи и используются для нахождения неизвестной величины. Они могут быть представлены числами, буквами или символами.

Неизвестная величина: это значение, которое нужно найти в задаче. Обычно она обозначается буквой или символом, отличным от известных величин.

Уравнение: это математическое выражение, в котором используются известные и неизвестная величины. Оно задает соотношение между величинами и позволяет найти значение неизвестной.

Решение уравнения: это процесс нахождения значения неизвестной величины, удовлетворяющего условиям задачи. Решение может быть представлено числом, дробью, процентом или другой формой.

Методы решения: это способы и приемы, которые применяются для нахождения значения неизвестной величины. К ним относятся алгебраические операции, преобразования уравнений, использование свойств чисел и прочие методы.

Проверка решения: это этап, на котором найденное значение неизвестной величины подставляется в уравнение или условия задачи для проверки его правильности.

Понимание основных понятий и методов решения задач по соотношению позволяет успешно справляться с такими задачами и применять математические знания на практике.

Применение соотношений в различных областях

Соотношения играют важную роль в решении задач в различных областях математики и физики. Они позволяют установить зависимость между различными величинами и использовать эту информацию для решения конкретных задач.

Один из примеров применения соотношений — задачи на пропорциональность. В таких задачах требуется найти неизвестную величину, зная ее пропорциональное отношение с другими известными величинами. Например, задачи на расчет скорости или расстояния могут быть решены с помощью соотношений.

Соотношения также широко применяются в физике. Например, в задачах на механику можно использовать законы Ньютона и различные соотношения между силой, массой и ускорением тела для решения задач о движении.

В геометрии соотношения также играют важную роль. Например, в задачах на подобие треугольников можно использовать соотношения между длинами сторон и соответствующими углами для решения задач о нахождении неизвестных сторон или углов.

В экономике соотношения также применяются для анализа данных и прогнозирования. Например, соотношения между объемом производства и затратами на производство позволяют оценить эффективность предприятия и принять решения о его развитии.

В искусстве соотношения используются для создания гармоничных и сбалансированных композиций. Например, золотое сечение — соотношение, используемое для создания пропорций идеальных форм в изобразительном искусстве.

ОбластьПримеры применения соотношений

Математика	Задачи на пропорциональность
Физика	Законы Ньютона, законы сохранения
Геометрия	Задачи на подобие треугольников, гармонические пропорции
Экономика	Анализ данных, прогнозирование
Искусство	Создание гармоничных композиций, использование золотого сечения

Вопрос-ответ:

Какие основные методы решения задач по соотношению в математике существуют?

Основные методы решения задач по соотношению в математике включают: метод подстановки, метод составления уравнений, метод графиков и метод пропорций.

Как использовать метод подстановки для решения задач по соотношению в математике?

Для использования метода подстановки нужно выбрать одну из переменных и подставить вместо нее известное значение. Затем рассчитать значение оставшейся переменной и проверить, удовлетворяет ли оно условиям задачи.

Как применить метод составления уравнений для решения задач по соотношению в математике?

Для применения метода составления уравнений нужно выразить неизвестные значения через переменные и записать уравнение, описывающее задачу. Затем решить полученное уравнение и найти значения переменных.

Как использовать метод графиков для решения задач по соотношению в математике?

Для использования метода графиков нужно построить график зависимости двух величин и найти точку пересечения графика с заданной прямой или кривой. Координаты этой точки будут являться решением задачи.

Как применять метод пропорций для решения задач по соотношению в математике?

Для применения метода пропорций нужно составить пропорцию, связывающую две величины, и решить ее. Для этого можно использовать свойство равенства долей и правило трех пропорций.

Методы решения задач по соотношению

Решение задач по соотношению может быть достаточно простым, если применить правильный метод. В этом разделе мы рассмотрим основные методы решения таких задач.

1. Метод пропорции: данный метод основывается на использовании пропорций для нахождения неизвестного значения в соотношении. Для этого необходимо составить пропорцию, в которой известные значения будут находиться на одной стороне, а неизвестное значение — на другой. После этого можно решить полученную пропорцию и найти неизвестное значение.
2. Метод подстановки: в этом методе мы подставляем известные значения в соотношение и решаем полученное уравнение для нахождения неизвестного значения. Этот метод особенно полезен, когда известны только два значения, а для нахождения третьего необходимо использовать соотношение.
3. Метод линейного уравнения: данный метод основывается на использовании уравнений вида y = kx + b, где y — зависимая переменная, x — независимая переменная, k — коэффициент пропорциональности, b — свободный член. В этом методе необходимо составить уравнение, учитывая известные значения и неизвестное значение, и решить его для нахождения неизвестного значения.
4. Метод системы уравнений: иногда для решения задач по соотношению требуется использовать систему уравнений. В этом случае необходимо составить систему уравнений, учитывая все известные значения и неизвестное значение, и решить ее для нахождения неизвестного значения.

Выбор метода решения задачи по соотношению зависит от конкретной ситуации и имеющихся данных. При решении задач рекомендуется внимательно прочитать условие, выделить известные и неизвестные значения, и выбрать наиболее подходящий метод для нахождения решения.

Примеры решения задач

Ниже приведены несколько примеров решения задач по соотношению в математике:

Пример 1:

Задача: В треугольнике ABC прямой угол при вершине C. Дано, что AC = 8 см, BC = 6 см. Найдите длину гипотенузы AB.

Решение: По теореме Пифагора в прямоугольном треугольнике гипотенуза равна квадратному корню из суммы квадратов катетов. Применяя эту формулу, получаем:

AB = √(AC² + BC²) = √(8² + 6²) = √(64 + 36) = √100 = 10 см.

Пример 2:

Задача: В определенный день сумма денег на счету Анны увеличилась в 3 раза, а на счету Бориса – в 5 раз. Если до этого сумма денег на счету Бориса была в 4 раза больше, чем на счету Анны, то на сколько процентов сумма денег на счету Бориса превышает сумму денег на счету Анны после увеличения?

Решение: Пусть исходная сумма денег на счету Анны равна А, а на счету Бориса – В. По условию задачи, В = 4А. После увеличения сумма денег на счету Анны станет 3А, а на счету Бориса – 5В. Таким образом, разница между суммами денег на счету Бориса и Анны будет равна 5В — 3А. Подставляя значения В и А, получаем:

5В — 3А = 5(4А) — 3А = 20А — 3А = 17А.

Для определения процента, на который сумма денег на счету Бориса превышает сумму денег на счету Анны, нужно выразить разницу в процентах от суммы денег на счету Анны:

Процент = (17А / 3А) * 100% = 5,67 * 100% = 567%.

Пример 3:

Задача: Найдите значение x в уравнении 2x — 5 = 11.

Решение: Для решения данного уравнения, нужно избавиться от коэффициента перед x. Для этого прибавим 5 к обеим частям уравнения:

2x — 5 + 5 = 11 + 5

2x = 16

Затем разделим обе части уравнения на 2:

2x / 2 = 16 / 2

x = 8.

Таким образом, значение x в уравнении 2x — 5 = 11 равно 8.

Типичные ошибки при решении задач по соотношению

При решении задач по соотношению в математике, многие учащиеся допускают некоторые типичные ошибки. Вот некоторые из них:

1. Неправильное определение переменных: Один из наиболее распространенных ошибок — неправильное определение переменных в задаче. Учащиеся могут сделать неправильные предположения о значениях переменных или неправильно выбрать переменные для решения задачи. Это может привести к неправильному ответу.

2. Неправильное составление уравнений: Другая распространенная ошибка — неправильное составление уравнений. Учащиеся могут неправильно записывать соотношения между переменными или игнорировать некоторые факты, которые могут быть важными для решения задачи. Это может привести к неправильным результатам.

3. Неправильное решение уравнений: Некоторые учащиеся могут неправильно решать уравнения, делая ошибки при вычислениях или пропуская некоторые шаги в процессе решения. Это может привести к неправильным ответам.

4. Неправильное толкование результата: Учащиеся могут неправильно толковать полученные результаты, что может привести к неправильным выводам или неправильному ответу на задачу.

5. Отсутствие проверки ответа: Некоторые учащиеся могут не проверять свои ответы после решения задачи. Это может привести к неправильным ответам, даже если все предыдущие шаги были выполнены правильно.

Избегайте этих типичных ошибок при решении задач по соотношению, обратите внимание на определение переменных, составление уравнений, решение уравнений и проверку ответов. Практика и внимательность помогут вам избегать этих ошибок и достичь правильных результатов.

Советы по успешному решению задач

Решение математических задач может быть сложным и требовать тщательного анализа. Вот несколько советов, которые помогут вам успешно решать задачи:

1. Внимательно прочитайте условие задачи. Особое внимание уделите ключевым словам и фразам, которые могут помочь вам понять, каким способом решать задачу.
2. Разберите задачу на более простые части. Попробуйте разложить ее на серию меньших задач, которые можно решить по отдельности.
3. Используйте подходящую математическую модель. Выберите соответствующие формулы, теоремы или методы, которые помогут вам решить задачу.
4. Проведите необходимые вычисления и приведите все значения к конечному ответу. Убедитесь, что вы правильно применили все математические операции.
5. Проверьте свое решение. Перепроверьте все шаги и убедитесь, что ваш ответ логически и математически корректен.
6. Постарайтесь найти альтернативные методы решения. Иногда существуют несколько способов решить задачу, и использование разных подходов может помочь вам лучше понять материал и улучшить ваши навыки.
7. Регулярно практикуйтесь в решении задач. Чем больше вы практикуетесь, тем лучше вы станете в решении математических задач.

Следуя этим советам, вы сможете улучшить свои навыки решения математических задач и получить лучшие результаты в учебе.

Роль соотношений в повседневной жизни

Одним из примеров использования соотношений в повседневной жизни является расчет времени. Мы используем соотношение между расстоянием, скоростью и временем, чтобы определить, сколько времени займет нам добраться из одного места в другое. Например, если мы знаем скорость движения автомобиля и расстояние, которое нужно преодолеть, мы можем использовать соотношение между ними, чтобы рассчитать, сколько времени займет поездка.

Соотношения также широко используются в финансовой сфере. Например, при расчете процентной ставки по кредиту или вкладу мы используем соотношение между суммой денег, сроком и процентной ставкой. Это помогает нам понять, сколько мы получим в результате вклада или сколько денег мы должны вернуть по кредиту.

Соотношения также применяются в науке и технике. Например, в физике мы используем соотношения между силой, массой и ускорением, чтобы определить движение тела. В инженерии соотношения помогают нам проектировать и строить различные устройства и конструкции, опираясь на взаимосвязь между различными параметрами.

Таким образом, соотношения играют важную роль в повседневной жизни, помогая нам разбираться во многих аспектах окружающего мира и принимать обоснованные решения.