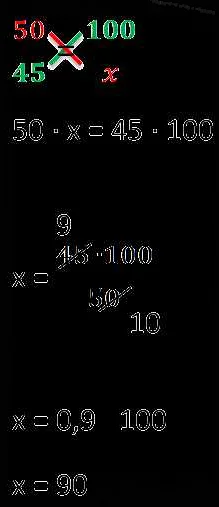Что такое соотношение в математике

Соотношение в математике — это понятие, которое указывает на связь, отношение или соответствие между двумя или более величинами, объектами или явлениями. Оно позволяет определить зависимость между этими элементами и использовать их для решения различных задач и задач. В математике соотношение может быть представлено в виде дроби, пропорции или уравнения. Понимание соотношения является важной основой для изучения многих разделов математики и научных дисциплин.

Соотношение – важное понятие в математике, которое позволяет установить отношение между двумя или более величинами. Это математическое выражение, которое связывает числа или переменные друг с другом и помогает определить их взаимосвязь. Соотношение может быть записано в виде уравнения, неравенства или пропорции.

Основное определение соотношения включает в себя несколько компонентов. Во-первых, есть величины, между которыми устанавливается отношение. Во-вторых, есть знак, который указывает, каким образом связаны эти величины. Например, знаки «равно», «больше», «меньше» и другие используются для обозначения соотношения. Кроме того, в соотношении также присутствуют числа или переменные, которые являются значениями этих величин.

Примером соотношения может служить уравнение «2x + 3 = 7», где x – неизвестное значение. Это соотношение устанавливает, что если умножить неизвестное значение x на 2, прибавить 3 и получить 7, то x равно 2.

Соотношения широко применяются в различных областях математики. Они играют важную роль в алгебре, геометрии, анализе данных и других разделах науки. С помощью соотношений можно решать уравнения и неравенства, находить значения переменных, а также анализировать и предсказывать различные явления и процессы.

Соотношение в математике: определение, примеры и применение

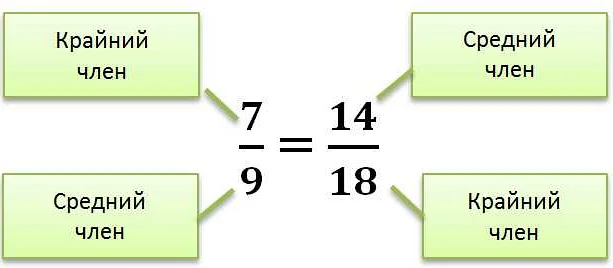
Соотношение может быть использовано для сравнения двух величин или для определения зависимости между ними. Оно позволяет выразить отношение между двумя частями целого или между двумя различными величинами.

Примеры соотношений:

Тип соотношенияПример

Равенство	2 + 2 = 4
Неравенство	5 > 3
Пропорция	3/5 = 6/10
Отношение	скорость = расстояние / время

Соотношения имеют широкое применение в математике и других науках. Они используются для решения уравнений, построения графиков, определения пропорций, анализа данных и многих других задач.

Понимание соотношений в математике позволяет установить связь между различными элементами и решать разнообразные проблемы и задачи.

Видео по теме:

Что такое соотношение в математике?

Соотношение может быть выражено различными способами. Например, в простейшем случае соотношение может быть записано в виде равенства, такого как 2 + 3 = 5. В этом примере левая и правая части равны, что означает, что две величины (2 + 3 и 5) равны друг другу.

Соотношение также может быть записано в виде неравенства, такого как 5 > 3. В этом примере левая часть (5) больше правой части (3), что означает, что одна величина больше другой.

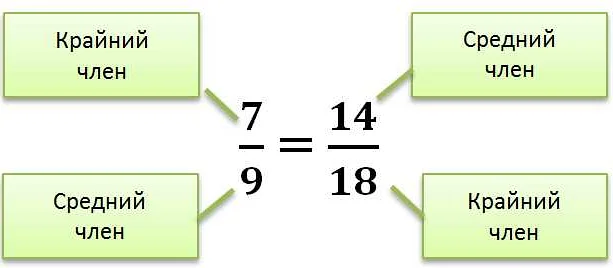
Пропорция — это особый вид соотношения, в котором две дробные выражения равны друг другу. Например, в пропорции 1/2 = 3/6, левая и правая части равны, что означает, что две величины (1/2 и 3/6) соотносятся между собой в определенном отношении.

Соотношения играют важную роль в математике и находят применение в различных областях, таких как алгебра, геометрия, физика и экономика. Они позволяют анализировать и описывать зависимости между различными величинами и решать разнообразные задачи.

Определение соотношения в математике

Соотношение в математике представляет собой выражение, устанавливающее связь между двумя или более величинами. Оно определяет, как одна величина зависит от другой и описывает их взаимодействие. Соотношение может быть представлено в виде уравнения, неравенства или функции.

В математическом соотношении обычно присутствуют переменные, которые представляют неизвестные или изменяющиеся величины. Задачей математика является изучение и анализ этих соотношений, чтобы найти значения переменных или установить свойства и закономерности между ними.

Примером математического соотношения может служить уравнение прямой в декартовой системе координат: y = mx + b. В этом соотношении переменные y и x представляют собой координаты точек на прямой, а m и b – коэффициенты, определяющие ее наклон и смещение. Это соотношение позволяет определить, как изменяется значение y в зависимости от значения x.

Соотношения в математике широко применяются для решения задач, моделирования реальных явлений и построения математических моделей. Они являются основой для многих математических дисциплин, таких как алгебра, геометрия, анализ и теория вероятностей.

ТерминОписание

Соотношение	Выражение, устанавливающее связь между двумя или более величинами.
Переменные	Неизвестные или изменяющиеся величины в математическом соотношении.
Уравнение	Вид соотношения, в котором два выражения равны друг другу.
Неравенство	Вид соотношения, в котором два выражения не равны друг другу.
Функция	Математический объект, определяющий зависимость между входными и выходными значениями.

Какие примеры соотношений существуют?

В математике существует множество примеров соотношений, которые используются для описания различных взаимосвязей и зависимостей между числами, объектами или явлениями. Некоторые из наиболее распространенных примеров соотношений включают:

• Пропорциональность: соотношение, при котором два набора чисел или величин связаны постоянным множителем. Например, если увеличение одной величины приводит к увеличению другой величины в том же отношении.
• Равенство: соотношение, при котором две величины или выражения равны между собой. Например, 2 + 3 = 5 или a + b = b + a.
• Неравенство: соотношение, при котором одна величина больше, меньше или не равна другой величине. Например, 5 > 3 или x < 10.
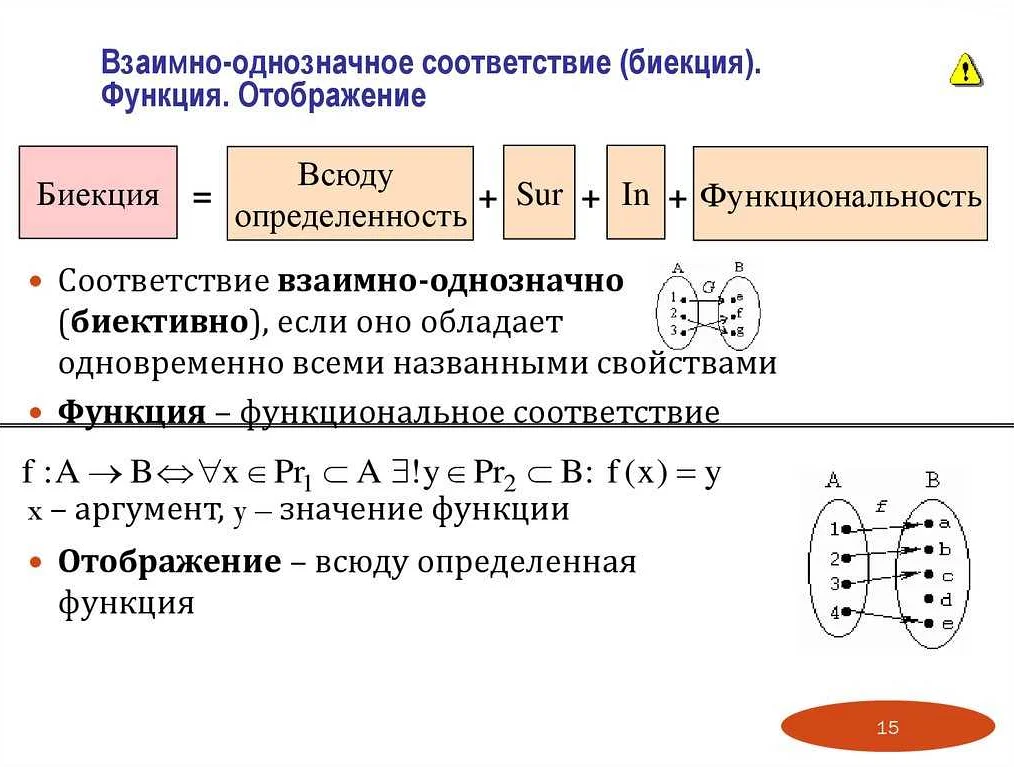
• Функциональная зависимость: соотношение, при котором каждому элементу из одного набора чисел (аргументу) соответствует один элемент из другого набора чисел (значению) в соответствии с определенным правилом или функцией.
• Процентное соотношение: соотношение, при котором одна величина или количество представляет определенную долю или процент от другой величины или общего количества.

Это лишь некоторые из примеров соотношений, используемых в математике. Каждый из них имеет свои особенности, применение и роль в решении различных задач и проблем.

Соотношение в пропорции

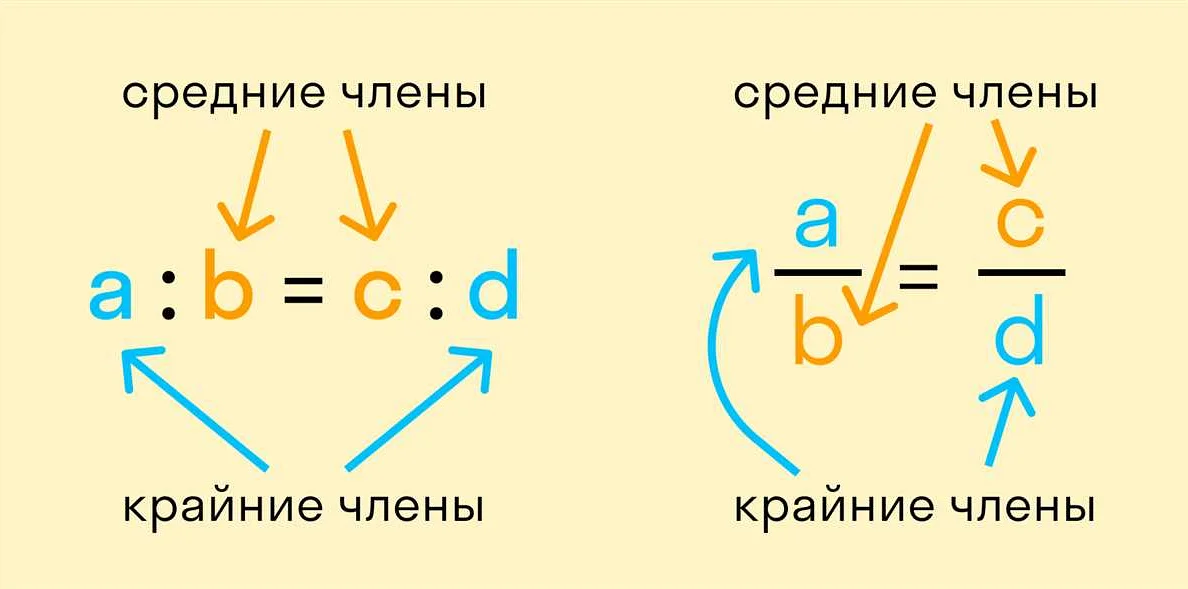
Пропорция обычно записывается в виде a:b = c:d, где a, b, c и d — числа. Здесь a и c образуют одну пару, а b и d — другую пару. Соотношение между этими парами остается неизменным.

Например, если a:b = 2:3, то это означает, что отношение между a и b равно отношению между 2 и 3. Это также означает, что если мы знаем значение a, мы можем найти значение b, умножив a на 3/2.

Пропорции широко используются в различных областях, таких как финансы, физика, геометрия и др. Они позволяют сравнивать и сопоставлять различные величины и отношения между ними.

Пропорции также могут быть сложными, с более чем двумя числами в каждой паре. Например, a:b:c = 2:3:4 означает, что отношение между a, b и c остается постоянным. Это позволяет решать сложные задачи, связанные с долей и соотношением различных величин.

Соотношение в уравнении

Примером соотношения в уравнении может быть простое уравнение вида:

x + 5 = 10,

где x — неизвестная величина. Чтобы найти значение x, необходимо провести ряд алгебраических операций:

x = 10 — 5 = 5.

Таким образом, значение x в данном уравнении равно 5.

Соотношение в уравнении широко применяется в различных областях математики, физики, экономики и других науках. Оно позволяет решать множество задач, связанных с нахождением неизвестных значений, определением зависимостей между величинами и анализом различных процессов и явлений.

Соотношение в процентах

Соотношение в процентах представляет собой один из способов выражения отношений между числами или величинами. Оно позволяет измерять, насколько одна величина больше или меньше другой, используя проценты.

Соотношение в процентах выражается в виде десятичной дроби или десятичного числа, умноженного на 100 и снабженного символом процента (%). Например, если у нас есть соотношение 0,75, то его можно выразить в процентах как 75%.

Соотношение в процентах широко используется во многих сферах, таких как финансы, экономика, статистика и торговля. Оно позволяет сравнивать данные, анализировать тренды и делать выводы о том, как одна величина влияет на другую.

Например, в финансовой отчетности компании можно использовать соотношение в процентах для анализа доходности или рентабельности. В торговле соотношение в процентах может использоваться для определения скидок или наценок на товары.

Соотношение в процентах также полезно при работе с вероятностями или статистическими данными. Например, если у нас есть данные о проценте выигрышей или поражений в спортивной команде, мы можем использовать соотношение в процентах для анализа и сравнения результатов.

Важно помнить, что соотношение в процентах всегда относится к какой-то базовой величине или значению. Например, если говорится о росте на 10%, это значит, что величина увеличилась на 10% от исходного значения.

В заключение, соотношение в процентах является полезным инструментом для выражения отношений между числами или величинами. Оно позволяет наглядно представить информацию, сравнивать данные и делать выводы на основе процентного отношения.

Применение соотношения в математике

Одно из основных применений соотношения — решение задач на пропорциональность. Например, при дележе какой-либо суммы между несколькими людьми, можно использовать соотношение для определения части, которая достанется каждому.

Соотношение также используется для решения задач на подобие. Например, если у нас есть два подобных треугольника, мы можем использовать соотношение длин сторон, чтобы найти соответствующие значения.

Другой областью применения соотношения является расчет пропорций и процентов. Например, при расчете налогов или скидок, мы можем использовать соотношение для определения итоговой суммы.

Соотношение также находит свое применение в физике, химии и других естественных науках. Оно помогает установить зависимость между различными физическими величинами и использовать их для проведения экспериментов и расчетов.

Таким образом, соотношение играет важную роль в математике и имеет широкий спектр применения в различных областях знания.

Вопрос-ответ:

Зачем нужно соотношение в математике?

Соотношение в математике используется для описания и анализа взаимосвязей между различными величинами. Оно позволяет установить зависимости между объектами и выражается в виде равенства или неравенства.

Что такое соотношение в математике?

Соотношение в математике представляет собой равенство или неравенство между двумя или более математическими выражениями. Оно позволяет установить взаимосвязи между величинами и решать различные задачи, связанные с математическим моделированием и анализом данных.

Какие примеры соотношений существуют в математике?

Существуют различные примеры соотношений в математике. Например, пропорциональность, когда две величины изменяются в одной и той же пропорции. Также, уравнения и неравенства являются примерами соотношений, где два выражения сравниваются на равенство или неравенство.

Как применяются соотношения в математике?

Соотношения в математике применяются для решения различных задач и моделирования реальных ситуаций. Они помогают анализировать и описывать взаимосвязи между различными величинами, проводить прогнозы и оптимизировать процессы. Соотношения находят применение в физике, экономике, биологии, статистике и других областях науки.

Какими свойствами обладают соотношения в математике?

Соотношения в математике обладают такими свойствами, как рефлексивность (любое выражение равно самому себе), симметричность (если A равно B, то B равно A), транзитивность (если A равно B, и B равно C, то A равно C). Также соотношения могут быть сопоставимыми (одно из двух выражений больше или меньше другого) или несопоставимыми (ни одно из выражений не больше или не меньше другого).

Какое определение соотношения в математике?

Соотношение в математике — это утверждение о равенстве или неравенстве двух математических выражений. Оно может быть записано в виде равенства, неравенства или другой математической формулы.

Какие примеры соотношений можно привести?

Примерами соотношений могут служить уравнения вида «x + 5 = 10», «2y > 8», «a^2 + b^2 = c^2», где x, y, a, b, c — переменные или константы. Эти примеры демонстрируют равенство или неравенство двух выражений.