Найти математическое ожидание суммы числа очков которые могут выпасть при бросании 2 костей

Узнайте, как найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух костей. Простые шаги и формулы для рассчета математического ожидания в математике и статистике.

Математическое ожидание является одним из основных понятий в теории вероятностей. Оно позволяет определить среднее значение случайной величины, которая может принимать различные значения с определенными вероятностями. В данной статье рассмотрим, как вычислить математическое ожидание суммы очков при бросании двух костей.

Бросание двух костей является простым экспериментом, который можно использовать для моделирования случайной величины. При каждом броске каждая кость может выпасть на одну из шести граней, пронумерованных от 1 до 6. Таким образом, общее количество возможных исходов равно 6*6=36.

Для вычисления математического ожидания суммы очков при бросании двух костей необходимо определить все возможные значения суммы и их вероятности. Например, сумма очков может быть равна 2, 3, 4 и т.д. Вероятность каждого значения суммы можно вычислить, разделив количество благоприятных исходов на общее количество исходов.

Например, чтобы определить вероятность суммы очков, равной 7, необходимо определить количество исходов, при которых выпадает пара костей с суммой 7 (6 и 1, 5 и 2, 4 и 3 и т.д.), и разделить его на общее количество исходов (36). Таким образом, вероятность суммы очков, равной 7, равна 6/36 = 1/6.

После определения всех возможных значений суммы очков и их вероятностей, необходимо умножить каждое значение на соответствующую вероятность и сложить полученные произведения. Результатом будет математическое ожидание суммы очков при бросании двух костей.

Основные понятия вероятности и математического ожидания

Вероятность — это числовая характеристика случайного события, которая выражает степень его возможности или невозможности. Она измеряется от 0 до 1, где 0 означает невозможность события, а 1 — его абсолютную достоверность. Вероятность события A обозначается P(A) и определяется как отношение числа благоприятных исходов к общему числу возможных исходов.

Математическое ожидание — это среднее значение случайной величины, которое ожидается в результате проведения серии экспериментов. Оно вычисляется путем умножения каждого возможного значения случайной величины на его соответствующую вероятность и сложения полученных произведений. Математическое ожидание обозначается E(X) или μ.

В случае с бросанием двух костей, сумма очков является случайной величиной. Для вычисления ее математического ожидания необходимо знать вероятности всех возможных исходов. Например, при бросании двух шестигранных костей, сумма очков может быть от 2 до 12. Вероятность каждой суммы можно вычислить, разделив количество благоприятных исходов на общее количество возможных исходов. Затем каждую сумму умножают на ее вероятность и полученные произведения складывают, чтобы получить математическое ожидание.

Что такое математическое ожидание суммы очков

Для вычисления математического ожидания суммы очков при бросании двух костей, необходимо знать все возможные комбинации результатов бросков и вероятности их появления. Например, при бросании двух шестигранных костей, на каждой из них может выпасть число от 1 до 6. Сумма очков будет варьироваться от 2 до 12.

Для вычисления математического ожидания суммы очков, необходимо умножить каждую возможную сумму очков на ее вероятность появления, а затем сложить полученные произведения. Например, если сумма очков 2 может появиться только при выпадении двух единиц, вероятность этого события равна 1/36. Сумма очков 3 может появиться при выпадении единицы и двойки или двух единиц, вероятность каждого из этих событий равна 2/36. И так далее для всех возможных сумм очков.

Вычисляя математическое ожидание суммы очков, мы получаем среднее значение, которое можно ожидать при множественных бросках. Например, для двух шестигранных костей, математическое ожидание суммы очков равно 7.

Математическое ожидание суммы очков является важным понятием в теории вероятностей, и его вычисление позволяет предсказать средний результат при случайных событиях, таких как бросание костей или другие игры, где важна сумма очков.

Какие значения может принимать сумма очков при бросании двух костей

При бросании двух шестигранных костей, сумма очков может принимать значения от 2 до 12.

Ниже приведен список всех возможных значений суммы очков:

• Сумма 2 может быть получена только при выпадении двух единиц на костях;
• Сумма 3 может быть получена двумя способами: 1+2 и 2+1;
• Сумма 4 может быть получена тремя способами: 1+3, 2+2 и 3+1;
• Сумма 5 может быть получена четырьмя способами: 1+4, 2+3, 3+2 и 4+1;
• Сумма 6 может быть получена пятью способами: 1+5, 2+4, 3+3, 4+2 и 5+1;
• Сумма 7 может быть получена шестью способами: 1+6, 2+5, 3+4, 4+3, 5+2 и 6+1;
• Сумма 8 может быть получена пятью способами: 2+6, 3+5, 4+4, 5+3 и 6+2;
• Сумма 9 может быть получена четырьмя способами: 3+6, 4+5, 5+4 и 6+3;
• Сумма 10 может быть получена тремя способами: 4+6, 5+5 и 6+4;
• Сумма 11 может быть получена двумя способами: 5+6 и 6+5;
• Сумма 12 может быть получена только при выпадении двух шестерок на костях.

Таким образом, всего существует 11 возможных значений суммы очков при бросании двух костей.

Как вычислить вероятность каждой суммы очков

Чтобы вычислить вероятность каждой суммы очков при бросании двух костей, необходимо учесть все возможные комбинации.

Всего существует 36 различных комбинаций двух костей, так как каждая кость имеет 6 вариантов выпадения (от 1 до 6). Перебрав все возможные комбинации, мы можем вычислить вероятность каждой суммы очков.

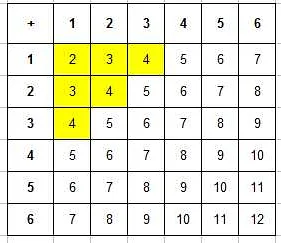
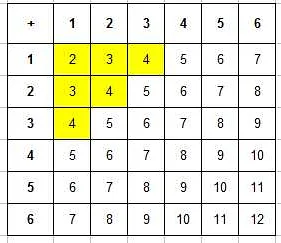
Для удобства, можно воспользоваться таблицей, где по горизонтали и вертикали указаны значения каждой кости, а в ячейках таблицы указана сумма значений. Ниже приведена таблица, которая показывает все возможные суммы очков и количество комбинаций, дающих данную сумму:

Сумма очковКоличество комбинаций

2	1
3	2
4	3
5	4
6	5
7	6
8	5
9	4
10	3
11	2
12	1

Для вычисления вероятности каждой суммы очков, нужно разделить количество комбинаций, дающих данную сумму, на общее количество комбинаций (36). Например, для суммы 2 есть только 1 комбинация, так что вероятность равна 1/36.

Вычислив вероятность для каждой суммы очков, можно построить график или список вероятностей для наглядного представления данных.

Таким образом, вычислить вероятность каждой суммы очков при бросании двух костей можно, учитывая все возможные комбинации и деля количество комбинаций, дающих данную сумму, на общее количество комбинаций.

Формула для вычисления математического ожидания

Формула для вычисления математического ожидания имеет следующий вид:

E(X) = Σ(x * P(x))

Где:

• E(X) — математическое ожидание случайной величины X
• x — значение случайной величины X
• P(x) — вероятность появления значения x

В случае бросания двух костей, сумма очков может принимать значения от 2 до 12. Для каждого значения суммы очков необходимо вычислить вероятность его появления.

Например, для значения суммы очков равной 7, существует 6 комбинаций, которые могут привести к такому результату: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1). Вероятность появления суммы очков 7 равна 6/36 или 1/6.

Применяя формулу, мы можем вычислить математическое ожидание суммы очков при бросании двух костей.

Видео по теме:

Вопрос-ответ:

Какие значения можно получить при бросании двух костей?

При бросании двух костей можно получить значения от 2 до 12.

Чему равно математическое ожидание суммы очков при бросании двух костей?

Математическое ожидание суммы очков при бросании двух костей равно 7.

Как вычислить математическое ожидание суммы очков при бросании двух костей?

Чтобы вычислить математическое ожидание суммы очков при бросании двух костей, нужно найти среднее арифметическое всех возможных значений суммы очков. Для этого нужно умножить каждое возможное значение суммы очков на вероятность его получения и сложить все результаты.

Какие значения суммы очков наиболее вероятны при бросании двух костей?

Наиболее вероятными значениями суммы очков при бросании двух костей являются 7 и 8. Эти значения имеют наибольшую вероятность выпадения.

Пример вычисления математического ожидания

Для вычисления математического ожидания суммы очков при бросании двух костей, необходимо знать вероятности выпадения каждой возможной комбинации.

Рассмотрим случай с обычными шестигранными костями. Каждая кость имеет 6 граней с числами от 1 до 6. Всего возможных комбинаций при бросании двух костей — 36 (6 граней на первой кости умножить на 6 граней на второй кости).

Чтобы вычислить вероятность выпадения каждой комбинации, нужно узнать, сколько комбинаций дают сумму 2, сколько — 3 и так далее до 12. Например, чтобы получить сумму 2, есть всего одна комбинация: на первой кости выпадает 1, на второй — 1. Для суммы 3 также есть только одна комбинация: 1 и 2 или 2 и 1.

Таблица вероятностей для всех комбинаций:

Сумма очковВероятность

2	1/36
3	2/36
4	3/36
5	4/36
6	5/36
7	6/36
8	5/36
9	4/36
10	3/36
11	2/36
12	1/36

Чтобы вычислить математическое ожидание, нужно умножить каждую сумму на ее вероятность и сложить результаты:

(2 * 1/36) + (3 * 2/36) + (4 * 3/36) + (5 * 4/36) + (6 * 5/36) + (7 * 6/36) + (8 * 5/36) + (9 * 4/36) + (10 * 3/36) + (11 * 2/36) + (12 * 1/36) = 7

Таким образом, математическое ожидание суммы очков при бросании двух костей равно 7. Это означает, что в среднем можно ожидать, что сумма выпадет равной 7 при множестве бросков.

Особенности вычисления математического ожидания в случае суммы очков

Для вычисления математического ожидания суммы очков необходимо учесть следующие особенности:

1. Дискретный характер величины. Сумма очков находится в диапазоне от 2 до 12, при этом все возможные значения являются дискретными. Это означает, что вероятность получить каждое из значений конечна и задается дискретным распределением.

2. Равномерное распределение. При бросании двух костей, каждая из них имеет 6 граней с числами от 1 до 6. Вероятность выпадения каждого значения на любой кости одинакова и равна 1/6. Таким образом, сумма очков также имеет равномерное распределение.

3. Свойства математического ожидания. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий. В данном случае, каждая из двух случайных величин соответствует выпавшему значению на одной из костей. Таким образом, математическое ожидание суммы очков равно сумме математических ожиданий значений на каждой из костей.

Итак, для вычисления математического ожидания суммы очков при бросании двух костей достаточно найти среднее арифметическое всех возможных значений на каждой из костей. В данном случае, оно равно (1+2+3+4+5+6)/6 = 3.5.

Таким образом, математическое ожидание суммы очков при бросании двух костей равно 7.