Найти математическое ожидание произведения числа очков которые могут выпасть при одном бросании двух

Узнайте, как найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух кубиков. Это позволит вам лучше понять вероятностные свойства этой игры и принять более информированные решения при различных игровых ситуациях.

Математическое ожидание – это понятие из теории вероятностей, которое позволяет предсказать среднее значение случайной величины. В данной статье мы рассмотрим математическое ожидание произведения очков при бросании двух кубиков.

Кубики – это игральные предметы, имеющие на каждой грани от 1 до 6 очков. При бросании двух кубиков мы получаем два случайных числа от 1 до 6. Произведение этих чисел будет случайной величиной, которую мы и будем исследовать.

Чтобы посчитать математическое ожидание произведения очков, нужно умножить каждое возможное значение произведения на его вероятность и сложить полученные значения.

Например, при бросании двух кубиков возможны следующие значения произведения: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12. Для каждого из этих значений мы можем рассчитать вероятность его получения. Затем, умножив каждое значение на его вероятность и сложив полученные значения, мы найдем математическое ожидание произведения очков.

Расчет математического ожидания произведения очков при бросании двух кубиков имеет интересные приложения в различных областях, таких как статистика, финансы, игровая теория и другие. В этой статье мы рассмотрели основы этого понятия и показали, как его можно применить для предсказания среднего значения произведения очков при бросании двух кубиков.

Произведение очков при бросании двух кубиков

При бросании двух кубиков, каждый из которых имеет по 6 граней, существует 36 возможных комбинаций выпадения очков. Чтобы вычислить математическое ожидание произведения очков, нужно умножить каждую возможную комбинацию очков на вероятность ее выпадения и просуммировать все результаты.

Вероятность выпадения каждой комбинации определяется формулой: P = 1/36, где P — вероятность выпадения данной комбинации. Например, вероятность выпадения комбинации 1 и 1 равна 1/36.

Далее, нужно умножить каждую возможную комбинацию очков на соответствующую ей вероятность и просуммировать все результаты. Например, для комбинации 1 и 1, произведение очков будет равно 1, а его вероятность — 1/36. Таким образом, результат для этой комбинации будет равен 1/36 * 1 = 1/36.

Повторяя этот процесс для каждой возможной комбинации, мы получим все результаты. Затем нужно просуммировать эти результаты, чтобы найти математическое ожидание произведения очков при бросании двух кубиков.

Что такое произведение очков при бросании двух кубиков?

Произведение очков при бросании двух кубиков является математической функцией, которая умножает числа, выпавшие на каждом кубике, чтобы получить итоговое число. Например, если на первом кубике выпало число 3, а на втором — число 4, то произведение этих двух чисел будет равно 12.

Математическое ожидание произведения очков при бросании двух кубиков представляет собой среднее значение всех возможных результатов умножения пар чисел, выпавших на кубиках. Для расчета математического ожидания нужно умножить каждую пару чисел, выпавших на кубиках, на их вероятности выпадения и сложить полученные значения.

Произведение очков при бросании двух кубиков является одним из аспектов, которые могут быть использованы в различных играх и задачах, связанных с вероятностями и математикой. Зная математическое ожидание произведения очков, можно прогнозировать и анализировать результаты игры или вероятность выпадения определенного числа.

Как рассчитать математическое ожидание произведения очков?

Математическое ожидание произведения очков при бросании двух кубиков можно рассчитать, используя теорию вероятностей. Для начала необходимо определить все возможные исходы при бросании двух кубиков. Каждый кубик имеет шесть граней с числами от 1 до 6. Таким образом, всего возможно 36 комбинаций выпадения чисел.

Далее необходимо определить вероятность каждого исхода. Вероятность выпадения каждой комбинации чисел равна 1/36, так как каждая комбинация равновероятна.

Для рассчета математического ожидания произведения очков нужно умножить каждую комбинацию чисел на ее вероятность и сложить результаты. То есть, необходимо умножить каждую комбинацию чисел на 1/36 и сложить полученные произведения.

Пример рассчета математического ожидания:

Математическое ожидание = (1 * 1/36) + (2 * 2/36) + (3 * 3/36) + … + (36 * 1/36).

После сложения всех произведений, полученная сумма будет являться математическим ожиданием произведения очков при бросании двух кубиков.

Формула для вычисления математического ожидания произведения очков

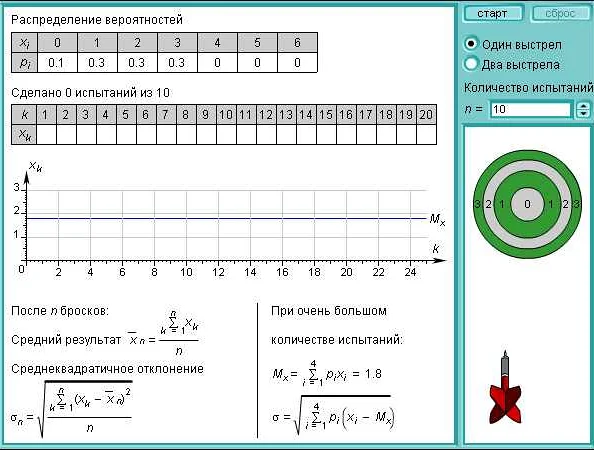
Предположим, что мы бросаем два кубика, каждый из которых имеет по 6 граней, на которых записаны числа от 1 до 6. Очки на каждом кубике будем обозначать как X и Y. Тогда произведение очков можно обозначить как Z = X * Y.

Для вычисления математического ожидания произведения очков необходимо рассмотреть все возможные комбинации значений X и Y и умножить каждую пару значений на соответствующую вероятность. Вероятность каждой комбинации можно рассчитать, разделив количество благоприятных исходов на общее количество возможных исходов.

Таким образом, формула для вычисления математического ожидания произведения очков выглядит следующим образом:

E(Z) = Σ (X * Y) * P(X = x, Y = y)

где E(Z) — математическое ожидание произведения очков, Σ — знак суммы, X * Y — произведение очков, P(X = x, Y = y) — вероятность комбинации X = x и Y = y.

Эта формула позволяет точно вычислить математическое ожидание произведения очков при бросании двух кубиков и использовать его для анализа и принятия решений в различных ситуациях.

Как применить формулу для вычисления математического ожидания?

Математическое ожидание = сумма всех возможных значений * вероятность каждого значения

Для применения этой формулы к конкретному случаю бросания двух кубиков, необходимо определить все возможные значения и их вероятности.

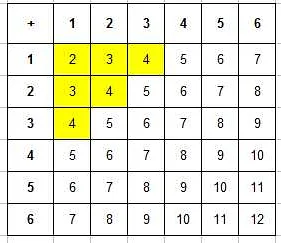
В данном случае, при бросании двух кубиков, возможные значения произведения очков будут от 2 до 12. Чтобы найти вероятность каждого значения, необходимо подсчитать количество способов получения этого значения и разделить на общее количество возможных комбинаций.

Например, для значения 2 есть только одна комбинация (1 и 1), поэтому вероятность этого значения равна 1/36. Для значения 3 есть две комбинации (1 и 2, 2 и 1), поэтому вероятность равна 2/36 и так далее.

После того, как найдены все значения и их вероятности, можно применить формулу и вычислить математическое ожидание произведения очков при бросании двух кубиков.

Пример вычисления:

Математическое ожидание = (2 * 1/36) + (3 * 2/36) + (4 * 3/36) + … + (12 * 1/36)

После подсчета всех значений, получается окончательное значение математического ожидания произведения очков при бросании двух кубиков.

Таким образом, используя формулу для вычисления математического ожидания и зная все возможные значения и их вероятности, можно определить среднее значение случайной величины. В данном случае, математическое ожидание позволяет нам определить ожидаемый результат при бросании двух кубиков.

Примеры вычисления математического ожидания произведения очков

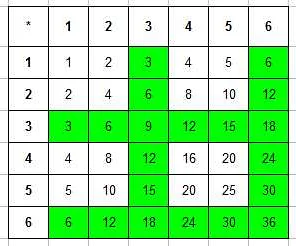
Математическое ожидание произведения очков при бросании двух кубиков может быть вычислено с помощью формулы:

Математическое ожидание произведения очков = Сумма всех возможных значений произведения очков × Вероятность каждого значения

Рассмотрим несколько примеров для наглядности:

Пример 1:

Пусть у нас есть два справедливых шестигранных кубика с числами от 1 до 6 на гранях. Найдем математическое ожидание произведения очков.

Сумма всех возможных значений произведения очков:

1 × 1 = 1

1 × 2 = 2

…

6 × 6 = 36

Всего возможных значений: 6 × 6 = 36.

Вероятность каждого значения равна 1/36, так как каждая пара значений на кубиках равновероятна.

Математическое ожидание произведения очков:

(1 × 1 + 2 × 2 + … + 6 × 6) × 1/36 = (1 + 4 + 9 + … + 36) × 1/36 = 91/6 ≈ 15.17

Пример 2:

Пусть у нас есть два несимметричных кубика, один с числами от 1 до 6, а другой с числами от 1 до 3. Найдем математическое ожидание произведения очков.

Сумма всех возможных значений произведения очков:

1 × 1 = 1

1 × 2 = 2

…

6 × 3 = 18

Всего возможных значений: 6 × 3 = 18.

Вероятность каждого значения зависит от соотношения чисел на кубиках. Например, вероятность получить 1 на первом кубике и 1 на втором кубике равна 1/18, так как есть только одна такая комбинация.

Математическое ожидание произведения очков:

(1 × 1 + 2 × 2 + … + 6 × 3) × 1/18 = (1 + 4 + 9 + … + 18) × 1/18 = 29/3 ≈ 9.67

Таким образом, математическое ожидание произведения очков при бросании двух кубиков может различаться в зависимости от чисел на кубиках и их вероятностей.

Вопрос-ответ:

Как рассчитать математическое ожидание произведения очков при бросании двух кубиков?

Математическое ожидание произведения очков при бросании двух кубиков можно рассчитать, умножив среднее значение выпавших очков на каждом кубике. Вероятность выпадения каждого числа на кубике равна 1/6. Среднее значение очков на одном кубике равно (1+2+3+4+5+6)/6 = 3.5. Поэтому математическое ожидание произведения очков будет равно 3.5 * 3.5 = 12.25.

Какие значения может принимать произведение очков при бросании двух кубиков?

Произведение очков при бросании двух кубиков может принимать значения от 1 до 36. На каждом кубике может выпасть одно из шести значений: 1, 2, 3, 4, 5 или 6. При умножении этих значений между собой, получаем все возможные произведения от 1 * 1 = 1 до 6 * 6 = 36.

Какова вероятность получить определенное значение произведения очков при бросании двух кубиков?

Вероятность получить определенное значение произведения очков при бросании двух кубиков зависит от количества способов, которыми можно получить это значение. К примеру, вероятность получить произведение 2 равна 1/36, так как есть только один способ получить это значение: на первом кубике выпало 1, на втором кубике выпало 2. Вероятность получить произведение 12 равна 1/36, так как также есть только один способ получить это значение: на первом кубике выпало 4, на втором кубике выпало 3. Вероятности для остальных значений можно рассчитать аналогичным образом.

Какова вероятность получить произведение очков, меньшее или равное определенному числу?

Вероятность получить произведение очков, меньшее или равное определенному числу, можно рассчитать суммируя вероятности получения каждого значения произведения, меньшего или равного этому числу. Например, для определенного числа 10, мы должны просуммировать вероятности получения произведений от 1 до 10. Каждая вероятность можно рассчитать, поделив количество способов получения этого значения на общее количество возможных исходов, которое равно 36. Таким образом, вероятность получить произведение очков, меньшее или равное 10, равна сумме вероятностей для значений 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10.

Значение математического ожидания произведения очков

Для определения значения математического ожидания произведения очков при бросании двух кубиков необходимо рассмотреть все возможные исходы. При бросании двух кубиков, общее количество возможных исходов равно 36 (6 возможных значений на первом кубике умноженные на 6 возможных значений на втором кубике).

Для каждого из этих исходов определяется произведение очков. Полученные значения произведения очков суммируются и делятся на общее количество исходов (36), чтобы получить среднее значение, которое и будет являться математическим ожиданием.

Первый кубикВторой кубикПроизведение очков

1	1	1
1	2	2
1	3	3
1	4	4
1	5	5
1	6	6
2	1	2
2	2	4
2	3	6
2	4	8
2	5	10
2	6	12
3	1	3
3	2	6
3	3	9
3	4	12
3	5	15
3	6	18
4	1	4
4	2	8
4	3	12
4	4	16
4	5	20
4	6	24
5	1	5
5	2	10
5	3	15
5	4	20
5	5	25
5	6	30
6	1	6
6	2	12
6	3	18
6	4	24
6	5	30
6	6	36

Сумма значений произведений очков равна 441. Разделив эту сумму на общее количество исходов (36), получаем среднее значение 12.25. Именно это значение является математическим ожиданием произведения очков при бросании двух кубиков.

Видео по теме: