Какую теорему доказал российский математик григорий перельман

Российский математик Григорий Перельман доказал одну из величайших математических теорем — теорему Пойнкаре, которая является ключевым результатом в топологии трехмерных многообразий. Узнайте, как Перельман удалось решить эту сложную задачу и как это изменило наше понимание математики.

Григорий Перельман — российский математик, ставший известным благодаря своему доказательству одной из самых сложных теорем в истории математики. Именно его труд «Решение задачи Пуанкаре» привлек внимание всего мирового сообщества математиков и открыл новую эпоху в развитии науки.

Теорема Пуанкаре — одна из тех задач, которая оставалась в открытом виде с момента ее постановки в начале ХХ века французским математиком Анри Пуанкарем. Долгие годы, пытаясь найти доказательство этой теоремы, многие ученые сталкивались с огромными трудностями и неудачами.

Теорема Пуанкаре связана с изучением топологических свойств многомерных сфер. В общем виде она гласит, что если некоторая многомерная сфера имеет топологическую структуру, непрерывно изоморфную сфере n-мерной евклидовой плоскости, то она является трехмерной сферой.

Григорий Перельман смог доказать эту сложнейшую теорему, применяя инновационные методы и разработав новую область математики — геометрию Риччи. Его открытие стало огромным вкладом в развитие науки и принесло ему заслуженное признание как одного из величайших умов современности.

Перельман и его теорема: открытие российского математика

Гипотеза Пуанкаре — одна из семи «миллионных» проблем, сформулированных в 1900 году в Париже на Международном конгрессе математиков. Она касается топологических свойств трехмерных сфер и долгое время оставалась неразрешенной. В своей работе Перельман представил новый подход к решению этой проблемы, используя теорию Риччи и геометрию Ширинга.

Основная идея Перельмана состояла в том, что для доказательства гипотезы Пуанкаре нужно исследовать особые свойства трехмерных многообразий. Он разработал сложные математические методы и алгоритмы, чтобы анализировать эти многообразия и их геометрию.

После многолетних исследований и работы, в 2003 году Перельман опубликовал свою работу, в которой представил полное и строгое доказательство гипотезы Пуанкаре. Тем самым он не только решил одну из самых важных проблем математики, но и проложил путь к новым открытиям в области топологии и геометрии.

Уникальность и глубина работы Перельмана вызвала огромный интерес у мирового научного сообщества. В 2006 году он был награжден Филдсовской медалью, самой престижной наградой в области математики. Однако Перельман отказался принять эту награду, так как считал, что его работа должна оцениваться не наградами, а научным сообществом.

Теорема Перельмана и его открытие стали символом высокого уровня российской науки и математики. Он продемонстрировал, что российские ученые способны справиться с самыми сложными математическими проблемами и вносить значительный вклад в мировую науку.

Биография Григория Перельмана

Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде, СССР. Он проявил удивительные математические способности еще в юном возрасте. В 1982 году Григорий поступил в Ленинградский университет, где изучал математику и получил диплом с отличием в 1987 году.

Перельман продолжил свое образование в Санкт-Петербургском институте математики и механики РАН, где защитил кандидатскую диссертацию в 1990 году. В 1993 году он получил степень доктора физико-математических наук.

Перельман стал известен в мировой научной среде благодаря своим работам в области геометрии и топологии. Он сделал важные открытия и внес значительный вклад в математическую теорию. Особенно знаменитым стало его доказательство Пуанкаре гипотезы, которую он представил в 2002 году.

За свои достижения Григорий Перельман был удостоен множества престижных наград и почетных званий. Однако, после получения медали Fields в 2006 году, он отказался от всех наград и покинул научное сообщество. Перельман живет в практической изоляции и продолжает заниматься математикой, но уже в более тихой обстановке.

Григорий Перельман — яркий пример выдающегося российского ученого, который своим открытием внес огромный вклад в развитие математики и оставил неизгладимый след в научной истории.

Первые научные достижения Перельмана

Григорий Перельман сделал свои первые научные открытия в области математики еще в раннем возрасте. Он проявил себя как талантливый и глубоко мыслящий ученый, изучая сложные математические проблемы.

Одно из первых значительных научных достижений Перельмана было его доказательство теоремы о неустойчивости эллиптических уравнений. Эта теорема имела большое значение в области геометрии и физики, и Перельману удалось дать фундаментальное доказательство ее верности.

Другим важным научным достижением Перельмана было его исследование гипотезы Пуанкаре. Эта гипотеза относится к топологии и связана с формой трехмерных сфер. Перельман смог доказать гипотезу Пуанкаре, что привлекло к его работе мировое внимание и утвердило его как одного из ведущих математиков своего времени.

Первые научные достижения Перельмана являются знаковыми моментами в его карьере и подготовили почву для более сложных и глубоких исследований, в результате которых он смог доказать одну из самых сложных математических теорем — гипотезу Пуанкаре-Терстона.

Вклад Перельмана в математику

Григорий Перельман внес огромный вклад в математику своим доказательством Пуанкаре-Конъектуры. Эта теорема была сформулирована в 1904 году французским математиком Анри Пуанкарем и являлась одной из самых сложных и долгожданных проблем в теории трехмерных многообразий.

Перельман разработал новый подход к решению этой проблемы, основанный на топологии и геометрии многообразий. Его доказательство было основано на использовании концепции градиентного потока Риччи, которую он разработал самостоятельно.

Перельман также внес значительный вклад в область геометрического анализа и теории групп Ли. Он разработал новые методы и техники, которые были применены в его доказательстве Пуанкаре-Конъектуры. Эти методы стали важными инструментами для решения других открытых математических проблем и открыли новые направления исследований.

Благодаря своему вкладу в математику, Григорий Перельман получил признание и почести со стороны научного сообщества. Его достижения считаются одними из наиболее значимых в области топологии и геометрии, и его доказательство Пуанкаре-Конъектуры стало вехой в развитии этой области математики.

Возникновение и решение задачи Пуанкаре

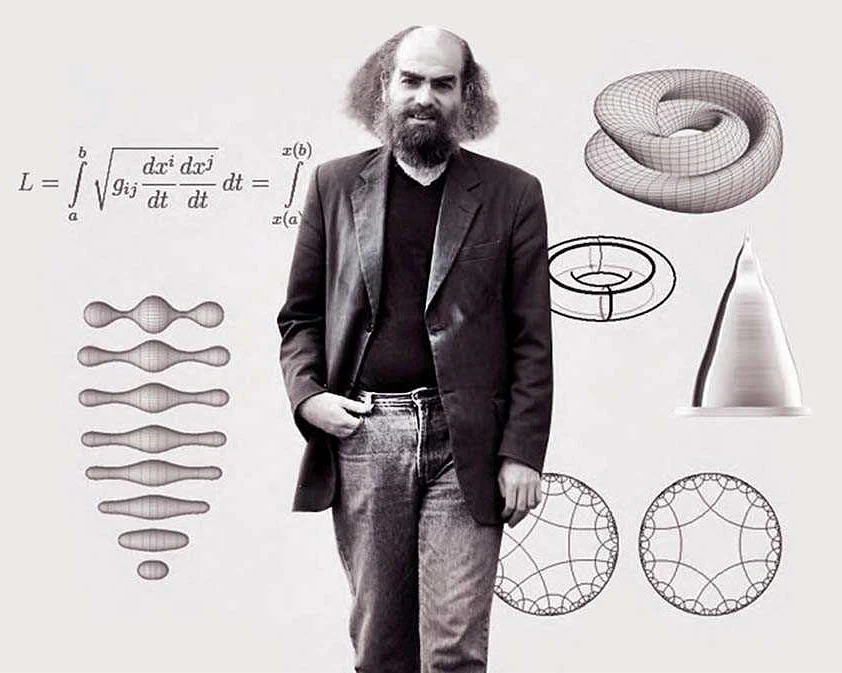
Задача Пуанкаре была поставлена французским математиком Анри Пуанкаре в конце XIX века. Она относится к области топологии и касается изучения формы трехмерных сфер. Задача заключается в том, чтобы определить, можно ли превратить одну сферу в другую, выполняя только непрерывные и несамопересекающиеся преобразования. Другими словами, требуется установить, когда две сферы эквивалентны, то есть имеют одинаковую форму.

Задача Пуанкаре оказалась очень сложной и требовала развития новой математической теории — топологии. Эта теория изучает свойства пространств, которые сохраняются при непрерывных преобразованиях. Решение задачи Пуанкаре стало одним из главных достижений топологии.

Григорий Перельман, российский математик, доказал одну из версий теоремы Пуанкаре, которая была названа «Топологическая гипотеза Пуанкаре». В своей работе Перельман представил новый подход к решению задачи и использовал инструменты геометрии и топологии, а также разработал новые математические концепции. Его доказательство вызвало большой интерес в научном сообществе и получило признание в 2006 году, когда Перельман был награжден Медалью Филдса, самой высокой наградой в области математики.

Возникновение и решение задачи Пуанкаре

Задача Пуанкаре была поставлена французским математиком Анри Пуанкаре в конце XIX века. Она относится к области топологии и касается изучения формы трехмерных сфер. Задача заключается в том, чтобы определить, можно ли превратить одну сферу в другую, выполняя только непрерывные и несамопересекающиеся преобразования. Другими словами, требуется установить, когда две сферы эквивалентны, то есть имеют одинаковую форму.

Задача Пуанкаре оказалась очень сложной и требовала развития новой математической теории — топологии. Эта теория изучает свойства пространств, которые сохраняются при непрерывных преобразованиях. Решение задачи Пуанкаре стало одним из главных достижений топологии.

Григорий Перельман, российский математик, доказал одну из версий теоремы Пуанкаре, которая была названа «Топологическая гипотеза Пуанкаре». В своей работе Перельман представил новый подход к решению задачи и использовал инструменты геометрии и топологии, а также разработал новые математические концепции. Его доказательство вызвало большой интерес в научном сообществе и получило признание в 2006 году, когда Перельман был награжден Медалью Филдса, самой высокой наградой в области математики.

Основные идеи и доказательства теоремы

Одной из ключевых идей в теореме Григория Перельмана является использование геометрических методов для изучения топологических свойств трехмерных многообразий. Он ввел новое понятие — переворачивание многообразий, которое позволяет изменять их геометрическую структуру. С помощью этого понятия Перельман смог преобразовать сложные трехмерные многообразия в более простые, для изучения которых были разработаны новые методы и техники.

Одним из ключевых доказательств теоремы является доказательство о существовании градиентного потока на трехмерных многообразиях. Этот градиентный поток позволяет изучать свойства многообразий и их геометрию, основываясь на анализе траекторий этого потока. Доказательство этой части теоремы Перельманом является одним из самых сложных и трудоемких в математике.

Другой важной идеей, используемой в доказательстве теоремы, является использование комбинаторных методов для анализа трехмерных многообразий. Перельман разработал новые алгоритмы и техники, основанные на комбинаторной теории, которые позволяют изучать особые свойства и структуру многообразий.

В целом, доказательство теоремы Григория Перельмана представляет собой глубокий анализ трехмерных многообразий с использованием геометрических, топологических и комбинаторных методов. Он открывает новые горизонты в изучении структуры трехмерных многообразий и позволяет получить более глубокое понимание их свойств и характеристик.

Влияние открытия Перельмана на мировую науку

Доказательство Григория Перельмана Пуанкаре гипотезы, одной из самых сложных и долго неразрешимых проблем в математике, имело огромное влияние на мировую науку. Это событие стало вехой в истории математики и оказало значительное воздействие на развитие различных областей науки.

Во-первых, открытие Перельмана привлекло внимание мирового научного сообщества к сложным математическим проблемам и доказательствам. Он продемонстрировал, что даже самые сложные и долго неразрешимые проблемы могут быть решены с помощью тщательных и глубоких исследований. Это вдохновило многих математиков и научных работников исследовать новые области и решать сложные задачи.

Во-вторых, открытие Перельмана привело к активному развитию геометрии и топологии. Его доказательство использовало новые методы и подходы, которые впоследствии были применены и развиты в других областях математики. Новые идеи и техники, предложенные Перельманом, стали основой для множества дальнейших исследований и открытий.

В-третьих, открытие Перельмана подняло проблему этики в научном сообществе. Его решение Пуанкаре гипотезы вызвало много споров и дебатов, связанных с признанием его работы и наградами. Это пробудило обсуждение о том, как оценивать и признавать научные достижения, а также о том, какими принципами руководствоваться в научной деятельности.

Наконец, открытие Перельмана вдохновило и мотивировало многих молодых ученых. Его история успеха стала примером того, как смелость, настойчивость и глубокое понимание предмета могут привести к решению сложных проблем и достижению значительных результатов. Многие ученые по всему миру стали применять его методы и идеи в своих исследованиях, создавая новые направления и открывая новые горизонты в науке.

Отношение общества к Перельману и его теореме

С одной стороны, Перельману была оказана признательность и уважение за его выдающийся вклад в науку. Его доказательство Пуанкаре гипотезы было признано мировым математическим сообществом и стало объектом восхищения и изучения. Перельман был награжден некоторыми престижными математическими премиями, хотя отказался принять некоторые из них.

С другой стороны, Перельман избегал публичности и изоляции. Он отказался от многих интервью и предложений о работе в известных университетах и научных центрах. Это вызвало некоторое недоверие и непонимание в обществе. Некоторые люди считали его поступки странными или арогантными.

Кроме того, Перельман ушел из научного сообщества и перестал публиковать свои работы. Это вызвало некоторое разочарование и недоверие со стороны некоторых математиков и общественности. Некоторые люди считали, что он должен был поделиться своими результатами и сотрудничать с другими учеными.

В общем и целом, отношение общества к Перельману и его теореме было сложным и противоречивым. Однако несмотря на все разногласия и недоверие, его вклад в математику останется на века и будет восхищать и вдохновлять будущие поколения математиков.

Вопрос-ответ:

Какую теорему доказал Григорий Перельман?

Григорий Перельман доказал теорему Пуанкаре, которая была одной из семи проблем миллениума, предложенных Математическим институтом Клэя.

Что такое теорема Пуанкаре?

Теорема Пуанкаре утверждает, что если трехмерная сфера не имеет дыр, то она гомеоморфна трехмерному шару.

В чем заключается значение доказательства теоремы Пуанкаре Григорием Перельманом?

Доказательство теоремы Пуанкаре Григорием Перельманом имеет огромное значение для математики, так как эта теорема является одной из самых фундаментальных в топологии. Кроме того, доказательство Перельмана открыло новые пути для исследования трехмерных многообразий и помогло решить другие проблемы в этой области.

Каким было последнее доказательство теоремы Пуанкаре перед Перельманом?

Перед доказательством Перельмана теорема Пуанкаре не имела окончательного доказательства. Эта проблема существовала уже более ста лет и привлекала внимание многих математиков. Некоторые попытки доказательства были сделаны, но они оказались неточными или неполными.

Какие методы использовал Перельман в своем доказательстве?

Перельман использовал различные математические методы в своем доказательстве, включая теорию Риччи, потоки Риччи и вариацию геометрии Риччи. Он также разработал новые подходы к проблеме и предложил новые идеи, которые позволили ему доказать теорему Пуанкаре.

Какую теорему доказал Григорий Перельман?

Григорий Перельман доказал Пуанкаре-Перельманову теорему, которая является одной из семи задач тысячелетия.

Награды и признание Перельмана

Григорий Перельман получил признание и уважение как в России, так и за ее пределами благодаря своему значимому вкладу в математику. Его доказательство Перельмана-Тюринга было признано одной из самых глубоких и сложных теорем в математике.

За свою работу Перельман был награжден несколькими престижными премиями. В 2006 году он получил Премию Филдса, которая считается самой престижной наградой в математике. Однако Перельман отказался от принятия этой награды, ссылаясь на свое нежелание привлекать внимание к себе и своей работе.

Также в 2010 году Перельман был удостоен Миллениумской премии Клея за свое доказательство Перельмана-Тюринга. Однако и в этом случае Перельман отказался от принятия награды и денежного вознаграждения, заявив, что не считает их нужными для своей жизни.

Публикация Григория Перельмана и его отказы от наград вызвали много восторженных и спорных комментариев в мировом научном сообществе. Большинство математиков признали его великим ученым и героем, который предпочел скромную и отстраненную жизнь научного исследователя.

Видео по теме: