Сколько теорем в математике: основные и знаменитые формулировки

Существует огромное количество теорем в математике, но точное количество неизвестно. Некоторые теоремы уже доказаны, другие же до сих пор являются гипотезами. Узнайте больше про мир математики и его теоремы в нашей статье.

Математика — это наука о числах, пространстве и форме. Во множестве разделов математики присутствуют теоремы, доказанные и освещенные специалистами за многие годы и подтвержденные на практике. Однако, не существует точных данных о количестве теорем, которые были доказаны на данный момент.

Какие же теоремы можно назвать основными в математике? Одной из наиболее известных теорем является теорема Пифагора, которая была доказана еще в Древней Греции и насчитывает более 100 доказательств. В математике также известна теорема Ферма, которая была доказана только после нескольких столетий работы математиков. Эта теорема звучит так: «Невозможно найти три положительных целых числа, удовлетворяющих уравнению x^n + y^n = z^n при n больше 2». Кроме того, в математике есть и множество других, не менее важных теорем, таких как теорема Ферма-Эйлера, теорема Пуанкаре, теорема Римана и многие другие.

Несмотря на то, что количество доказанных и подтвержденных теорем в математике велико, оно не является постоянным и постоянно растет благодаря усилиям талантливых математиков со всего мира.

Сколько теорем существует в математике?

Математика является наукой, в которой изучаются абстрактные и формальные отношения, структуры и понятия. Эта наука широко известна своими теоремами, которые являются важнейшей частью математического знания. Однако, как правило, просто невозможно определить точное число всех теорем, которые когда-либо были доказаны, и тем более их объем.

Существует огромное количество теорем в математике, и каждый день публикуются новые результаты и открытия. Среди самых основных теорем и результатов можно назвать теорему Пифагора, формулу Эйлера, теорему Ферма, теорему Пуанкаре, теорию вероятностей, алгебру, геометрию и анализ.

Теоремы в математике отличаются разной сложностью и важностью. Некоторые из них имеют широкое практическое применение в различных областях, включая науку, технологию, экономику, медицину и другие. Другие теоремы являются главным содержанием научных исследований и являются важной составляющей образования в области математики.

Таким образом, ответ на вопрос, сколько теорем существует в математике, неточен и зависит от конкретной области этой науки. Однако, можно утверждать, что их количество находится настолько высоком уровне, что математика справедливо называется одной из самых интересных и важных наук.

Видео по теме:

Основные теоремы

Математика — это наука о числах, формах и структурах. В математике существует множество теорем, которые являются основой для дальнейших математических исследований. Некоторые из них стали настолько известными, что стали носить имена ученых, которые их сформулировали или доказали.

• Теорема Пифагора — одна из наиболее известных теорем в математике, утверждающая, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
• Теорема Ферма — одна из самых долгожданных и сложных теорем в истории математики, которую Ферма сформулировал в XVI веке. Теорема утверждает, что для уравнения x^n + y^n = z^n простых чисел x, y и z не существует, если n больше 2.
• Теорема о трех перпендикулярах — одна из основных теорем геометрии, которая утверждает, что проходящие через одну точку и пересекающие прямую три прямые могут быть только перпендикулярами.
• Теорема Пуанкаре — теорема из области топологии, утверждающая, что 3-мерная сфера является единственным замкнутым 3-мерным многообразием со свойством сферы.
• Теорема Фейнмана-Дайсона-Шридингера — основополагающая теорема в квантовой механике, устанавливающая связь между двумя способами описания эволюции квантовых систем: уравнением Шредингера и интегральным уравнением Фейнмана-Дайсона.

История математических теорем

Математические теоремы, как и математика в целом, имеют богатую историю. Многие известные теоремы были открыты еще древними греками. Например, теорема Пифагора, которая была открыта греческим математиком Пифагором в VI веке до нашей эры. Она утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Другие известные теоремы были открыты в более поздние времена. Например, теорема Ферма, которая была доказана только в 1994 году, хотя ее формулировка была предложена уже в XVII веке французским математиком Пьером де Ферма. Эта теорема гласит, что уравнение x^n + y^n = z^n не имеет целочисленных решений, если n больше двух.

Интересно, что математические теоремы не всегда открывались сразу. Например, теорема Ферма оставалась нерешенной в течение нескольких столетий. Многие математики пытались доказать ее, но никому не удавалось. В конце концов, теорему удалось доказать британскому математику Эндрю Уайлсу.

Сегодня существует множество математических теорем, известных и менее известных. Некоторые из них имеют практическое применение, например, теорема Ферма-Эйлера, которая используется в криптографии. Другие теоремы имеют чисто теоретическое значение. В любом случае, математические теоремы остаются одним из самых интересных и значимых достижений человеческой мысли.

И это только вершина айсберга, ведь интенсивные исследования, проводимые в современной математике, продолжают поражать людские умы и увлечь всех, кто любит и понимает математику.

Вопрос-ответ:

Как много теорем существует в математике?

В математике существует огромное количество теорем — от классических, таких как Теорема Пифагора или Теорема Ферма, до современных теорем в вычислительной математике. Количество известных теорем не подлежит точному подсчету.

Какая теорема является самой известной?

Самой известной теоремой в математике является, вероятно, Теорема Пифагора.

Какие основные теоремы математики нужно знать?

Основные теоремы математики включают в себя Теорему Пифагора, Теорему Ферма, Диагональную Теорему Кантора-Бернштейна, Теорему Пуанкаре, Теорему о трех касательных, Гипотезу Римана и т.д.

Какие теоремы в математике имеют широкое практическое применение?

Теоремы Фурье, Теорема о наименьшем квадрате, Теорема Ньютона-Лейбница, Теорема Гаусса-Маркова — эти теоремы имеют широкое практическое применение в физике, экономике, инженерии и других областях науки.

Какие теоремы в математике имеют наибольшую сложность?

Одна из наиболее сложных теорем в математике — это Гипотеза Римана, которая до сих пор не была доказана. Также среди сложных теорем можно упомянуть Теорему Формулы Монстра, которая связывает теорию чисел и теорию групп ли, и Теорему Ферма-Вейля, которая имеет прямое отношение к арифметике эллиптических кривых.

Какие теоремы математики были решены в последнее время?

Одной из недавно решенных теорем является Проблема Продолговатости, которая была решена с помощью мощных вычислительных возможностей. Также в последнее время были решены Теоремы Фейнмана-Крауля и Теорема Перельмана.

Какие теоремы математики имеют самое длинное доказательство?

Самое длинное доказательство в современной математике имеет Теорема Четырех Красок, доказательство которой требует более 600 страниц. Другими длинными доказательствами являются доказательства Теоремы Ферма и Теоремы Пуанкаре.

Теоремы исчисления предикатов

Исчисление предикатов является важным разделом математической логики и используется во многих областях, включая информатику, философию и математику. В исчислении предикатов рассматриваются логические выражения, в которых присутствуют отношения между объектами.

Одной из основных теорем в исчислении предикатов является теорема Лёвенгейма-Сколема, которая говорит о возможности представления любой теории первого порядка в терминах теории множеств. Также важной теоремой является теорема Гёделя о полноте, утверждающая, что любая истинная формула исчисления предикатов может быть доказана в рамках данной теории.

Еще одной известной теоремой исчисления предикатов является теорема Хансена-Лоуэрд-Курцвейла, устанавливающая эквивалентность между разными системами исчисления предикатов. Также стоит отметить теорему Линденбаума о расширении, которая говорит о возможности расширения формальной системы логики до полной теории.

Наконец, следует упомянуть теорему Гёделя о неполноте, утверждающую, что в любой достаточно сложной формальной системе логики существуют истинные высказывания, которые не могут быть доказаны в рамках этой системы. Эта теорема имеет важное значение не только для математической логики, но и для фундаментальных вопросов о природе математики и ее возможностях.

Теоремы геометрии

Геометрия – это одна из наиболее изучаемых дисциплин математики, которая охватывает изучение свойств фигур и пространственных форм. Теоремы геометрии – это формулировки утверждений, которые представляют собой законы и правила, устанавливающие связи между элементами геометрических объектов.

Одной из известных теорем геометрии является теорема Пифагора. Она устанавливает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Эта теорема является основой для многих дальнейших изысканий и открытий в геометрии и математике в целом.

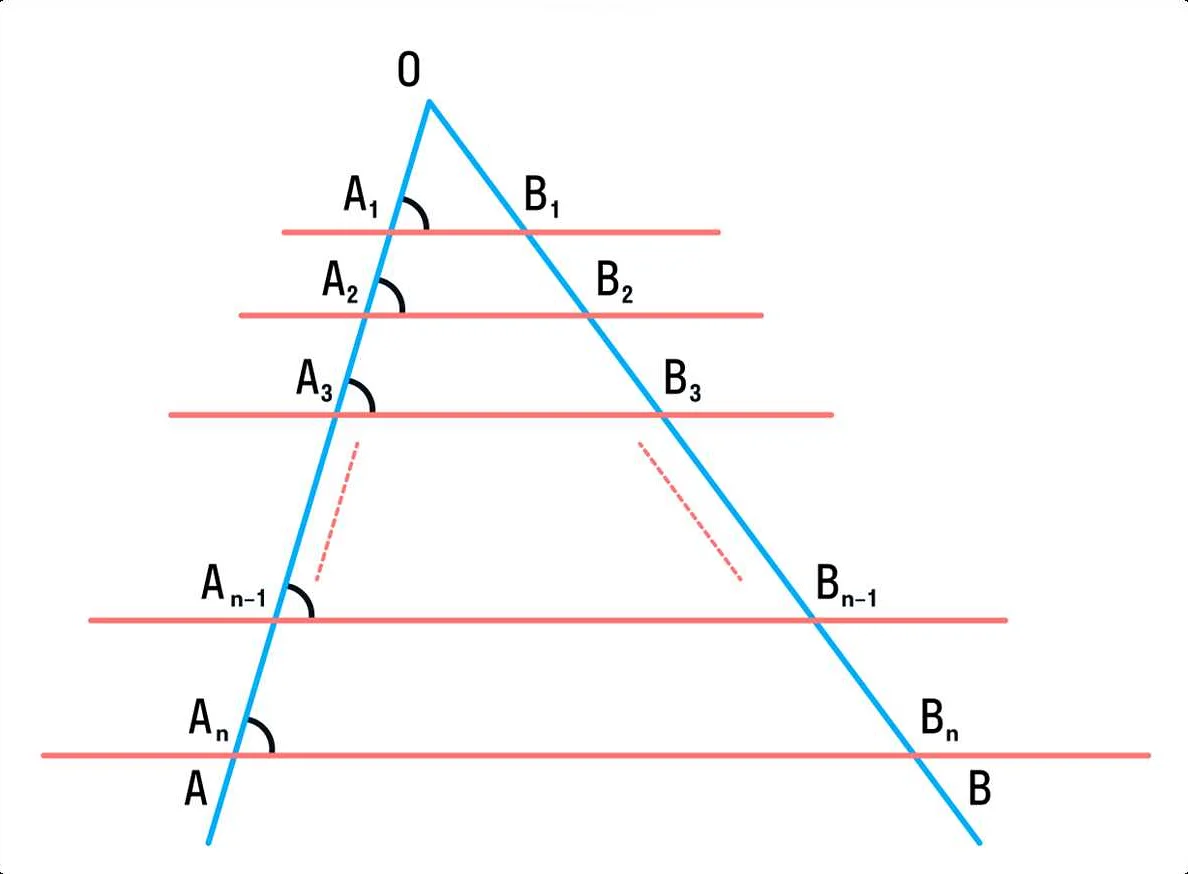
Другой известной теоремой является теорема Фалеса. Она устанавливает, что если провести сечение в треугольнике параллельно одной из его сторон, то пропорции отрезков, на которые это сечение делит другие стороны, будут равны.

Теорема Эйлера – одна из самых глубоких и важных теорем геометрии. Она устанавливает связь между числами вершин, ребер и граней многогранника. Теорема Эйлера позволяет понимать, как устроены многогранники и как они взаимодействуют друг с другом.

Также в геометрии существует множество других теорем, например, теорема о вписанном и описанном угле, теорема о трезубце, теорема тангенций и многие другие. Знание теорем геометрии – важный компонент в обучении математике и науке в целом.

Теоремы топологии

Топология – это раздел математики, который изучает свойства геометрических фигур, оставляя за бортом их размерности, меру и другие свойства, которые могут меняться при непрерывных преобразованиях. В топологии существует множество теорем, которые позволяют описывать и классифицировать топологические объекты. Рассмотрим несколько из них.

Теорема Пуанкаре-Хопфа говорит о количестве независимых решений системы нелинейных дифференциальных уравнений на сфере. Согласно этой теореме, количество решений равно сумме индексов двух векторных полей на сфере.

Теорема Шарковского устанавливает существование периодических траекторий в непрерывных динамических системах слишком сложного поведения. Она указывает на связь между порядком периодов траекторий и их структурой.

Теорема Буэнаха – это свойство компактности, которое характеризует замкнутость и ограниченность объекта. Теорема утверждает, что любое открытое покрытие компактного множества имеет конечное подпокрытие.

Теорема Брауэра говорит о том, что каждое непрерывное отображение шара в себя имеет неподвижную точку, то есть точку, которая не двигается при преобразовании.

Теорема Хопфа описывает многомерные объекты, которые являются объединением сфер и многомерных торов. Теорема утверждает, что если маппинг сфер на эти объекты сохраняет некоторые свойства, то он сохраняет их и на гипотетических объектах, которые еще не были изучены.

Это лишь некоторые из теорем топологии. Несмотря на свою абстрактность и сложность, топология находит широкое применение в науке и технике.

Теоремы групповой теории

Теорема Лагранжа – основополагающая теорема групповой теории, которая говорит о том, что порядок любой подгруппы конечной группы делит порядок группы.

Теорема Кэли — теорема алгебры, утверждающая, что каждую конечную группу можно задать как подгруппу группы перестановок элементов этой группы.

Теорема Силова – теорема групповой теории, которая говорит о том, что если порядок конечной группы является произведением степеней нескольких различных простых чисел, то эта группа содержит подгруппу мощности p^k для каждого простого делителя порядка группы.

Теоремы Фробениуса – ряд теорем групповой теории, которые относятся к разложению группы как произведения более простых групп, и используются в теории конечных групп и групповых представлениях.

Теорема факторизации Гильберта – теорема, которая описывает разложение группы линейных операторов над конечномерным векторным пространством над алгебраически закрытым полем на примарные циклические подгруппы, установленное Давидом Гильбертом.

Теоремы алгебры

Алгебра, как раздел математики, занимается изучением алгебраических структур, таких как группы, кольца и поля. В алгебре существует множество теорем, которые играют важную роль в понимании и решении задач в этой области.

Одной из наиболее известных теорем алгебры является теорема о том, что любой многочлен с комплексными коэффициентами имеет корень. Эта теорема была доказана в 1799 году Карлом Фридрихом Гауссом и является фундаментальной теоремой алгебры.

Другая важная теорема алгебры — теорема о гомоморфизмах, которая устанавливает связь между структурами алгебраических систем. Она помогает понимать, как связаны между собой группы, кольца и поля, и как они могут быть связаны с другими математическими структурами.

1. Теорема Лагранжа — описывает основные свойства группы и ее подгруппы.
2. Теорема Кэли — утверждает, что любая конечная группа может быть задана в виде группы перестановок.
3. Теорема Абеля-Руффини — устанавливает, что многочлен пятой степени или выше не может быть решен формулой.

Теоремы алгебры имеют множество приложений в различных областях, таких как криптография, теория чисел, физика, компьютерные науки и другие.

Теоремы функционального анализа

Функциональный анализ — это ветвь математического анализа, призванная изучать свойства коснтруируемых пространств функций и операторов, а также их взаимодействие. В рамках этой теории было сформулировано множество фундаментальных теорем, которые играют важную роль в приложении математического анализа во многих областях.

• Теорема Банаха-Штейнгауза: эта теорема формулирует условия ограниченности оператора;
• Теорема Хана-Банаха: это одна из ключевых теорем функционального анализа, которая позволяет продолжать линейные функционалы с нормированного пространства на еще более общее пространство;
• Теорема Фредгольма: эта теорема связывает решение однородного уравнения согласованности, с решением соответствующего неоднородного уравнения;
• Теорема Стоуна: теорема, связывающая все компактные пространства с пространствами непрерывных функций.

Кроме этих теорем, в функциональном анализе есть множество других, не менее важных теорем, таких, как теорема Рисса об интегральном представлении, теорема Гильберта-Шмидта, теорема Банаха о конечномерности пространства продолжаемых линейных операторов, теорема о трех сериях для локально конечных мер, и многие другие.

Теоремы числовой теории

Числовая теория — ветвь математики, которая изучает свойства и отношения между целыми числами. Она содержит множество интересных теорем, которые помогают решать различные математические задачи.

Среди этих теорем наиболее известная — теорема Ферма. Она была доказана в 1994 году Эндрю Уайлсом, и гласит, что уравнение xn+yn=zn не имеет целочисленных решений, кроме тривиальных случаев (n=1,2).

Еще одна известная теорема — теорема Вильсона. Она была сформулирована в 1770-х годах и утверждает, что если p — простое число, то (p — 1)! + 1 делится на p. В свою очередь, теорема Вильсона нашла применение в криптографии, где используется группа вычетов по простому модулю.

Необходимо также упомянуть теорему Дирихле, установленную Густавом Лебьегом Дирихле в 1837 году. Она утверждает, что в любой арифметической прогрессии с любым первым членом и любой ненулевой разностью найдется бесконечное множество простых чисел.

Также существует бесконечность простых чисел. Эту теорему впервые сформулировал Евклид в III веке до нашей эры. Смысл теоремы заключается в том, что не существует конечного числа простых чисел. Они простираются в бесконечность и дают основу для целочисленной арифметики.

Наконец, из числовой теории невозможно обойти утверждение, называемое «Проблемой Гольдбаха». Формулировка этой проблемы заключается в том, что каждое четное число можно представить в виде суммы двух простых чисел. Хотя эта проблема выглядит достаточно простой, до сих пор не существует математического доказательства ее верности.

Теоремы дифференциальной геометрии

Дифференциальная геометрия является разделом математики, который изучает гладкие поверхности и кривые, используя методы и инструменты алгебры и анализа. В этом разделе математики выделяются некоторые важные теоремы.

Теорема Гаусса-Бонне – это одна из фундаментальных теорем дифференциальной геометрии. Она рассказывает о связи между кривизной поверхности и интегралом поверхностного напряжения.

Теорема Римана-Роха – это еще одна важная теорема дифференциальной геометрии. Она определяет эквивалентные условия, которые гарантируют существование гладкой функции на кривой.

Теорема Стоукса – это формулировка основного закона сохранения, который относится к векторному полю. Теорема Стоукса утверждает, что интеграл по замкнутому контуру поверхностного напряжения векторного поля определяется интегралом по поверхности, ограниченной этим контуром.

Теорема Грина – это теорема из области математического анализа, которая устанавливает связь между криволинейным интегралом I косвенной (оставляющей циркуляцию) обычного дифференциала некоторой функции и двойным интегралом в области, ограниченной этой кривой.

Известные теоремы в науке

Математика — это наука о числах, структурах и пространстве. В ее основе лежат множество теорем, которые помогают понять и описать многие явления в природе и социуме. Некоторые из них так известны, что стали частью общекультурного наследия и перешли границы своей узкой предметной области.

Одной из таких теорем является теорема Ферма-Вайля. Она утверждает, что для любого целого положительного числа n больше 2 существует такие положительные целые числа x, y и z, что уравнение x^n + y^n = z^n не имеет решения. Эта теорема была сформулирована и доказана в XVII веке, но ее доказательство заняло более 300 лет. Она стала одной из самых сложных математических задач, которая была решена только в 1995 году.

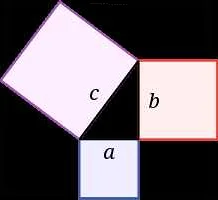
Еще одной известной теоремой является теорема Пифагора. Она утверждает, что для любых прямоугольных треугольников квадрат гипотенузы равен сумме квадратов катетов. Теорема получила свое название в честь греческого математика Пифагора, который открыл ее около 2500 лет назад. С тех пор она нашла многочисленные применения в геометрии, физике и других науках.

Теоремы Эйлера, Ньютона, Фурье, Римана, Пуанкаре и многих других математиков также знакомы не только математикам, но и широкому кругу людей. Они описывают законы движения тел, электромагнитные явления, течения жидкостей, формулы исчисления вероятностей и многое другое.

Таким образом, математические теоремы являются надежными инструментами для понимания и описания различных явлений в науке и жизни. Их знание и изучение являются необходимыми для развития науки и технологий.