Что такое классы и разряды в математике 5 класс

Классы и разряды в математике 5 класс – это основные понятия, которые помогут ученикам разобраться в составлении и чтении чисел, а также в проведении арифметических операций. Эта статья расскажет о том, как понять, что такое классы и разряды в математике и как они используются в повседневной жизни.

Классы и разряды — важные понятия в математике, которые изучаются в 5 классе. Они помогают нам понять, как организованы числа и как можно их обозначать. Классы и разряды позволяют нам работать с большими числами и разбираться в их структуре.

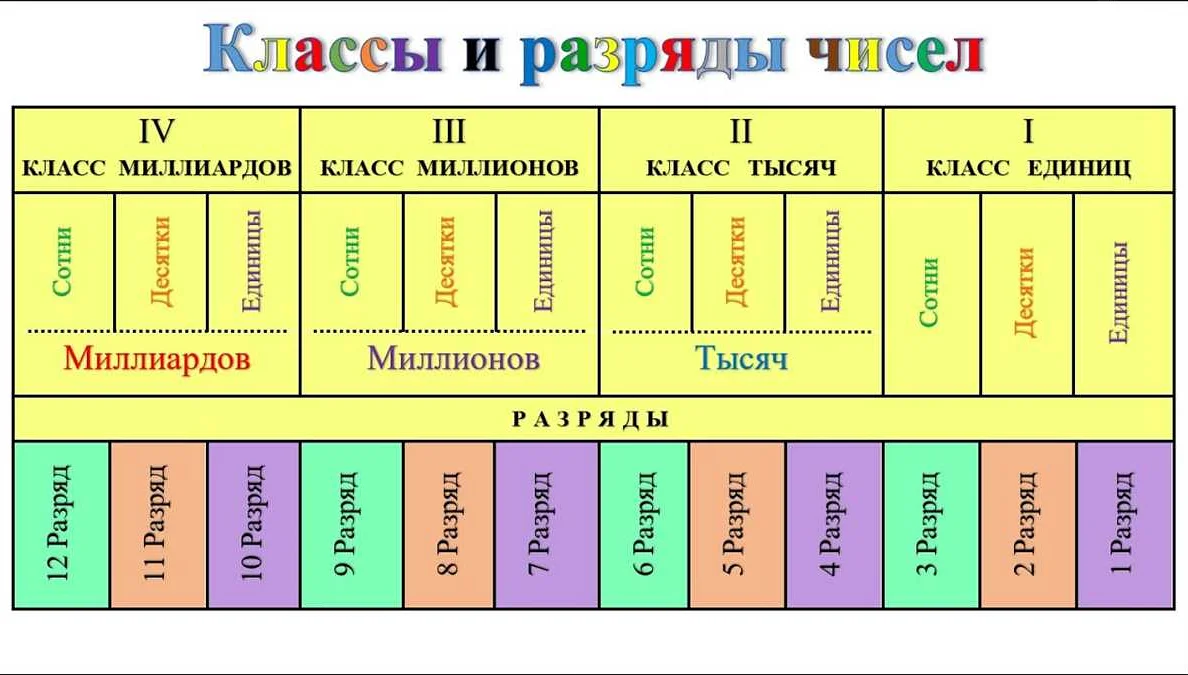
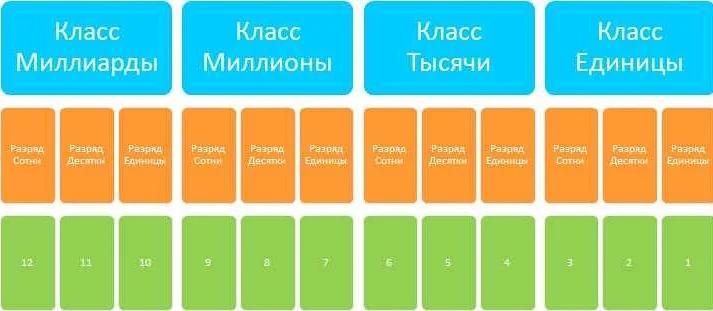
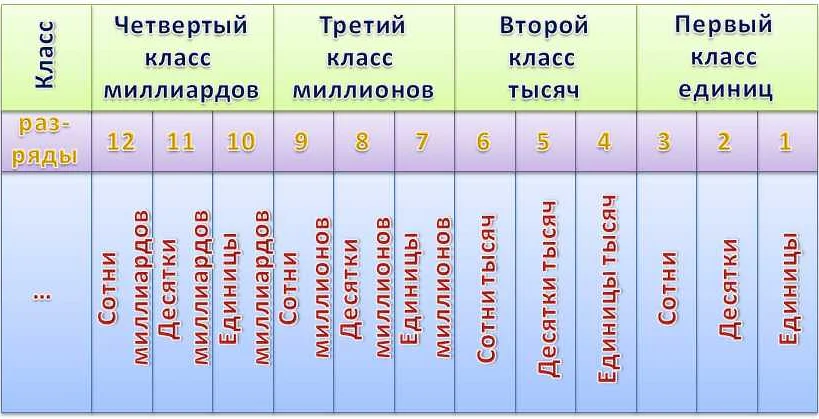
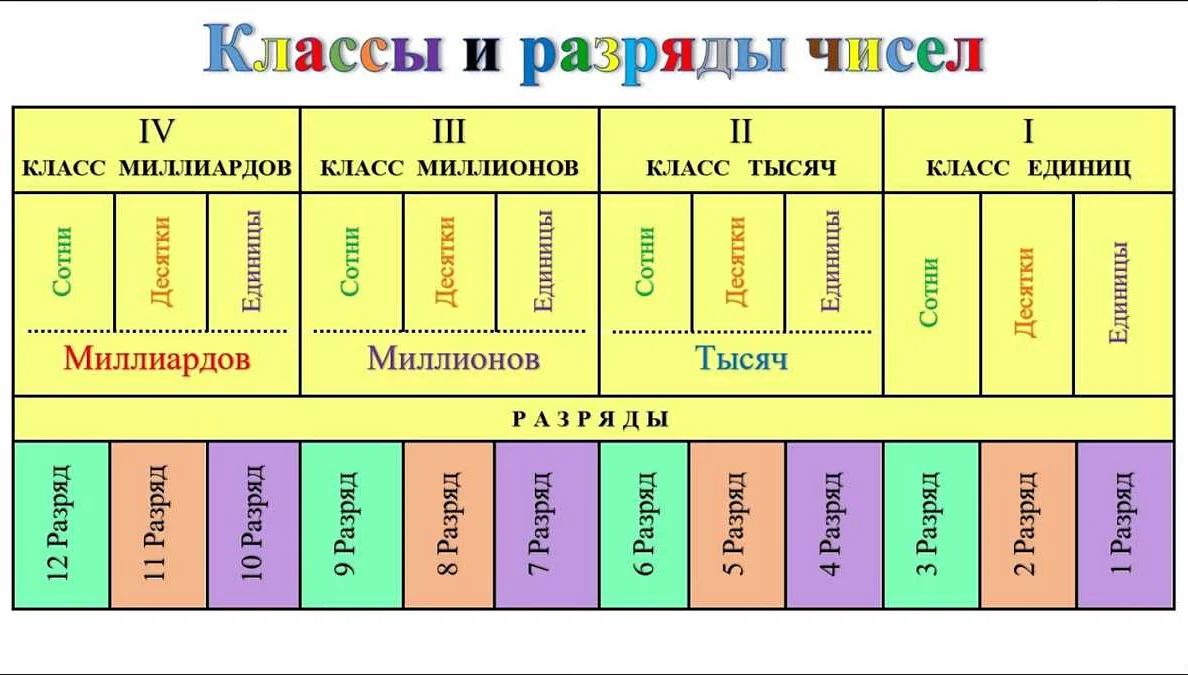
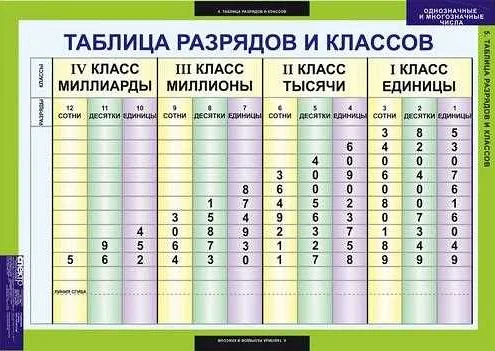
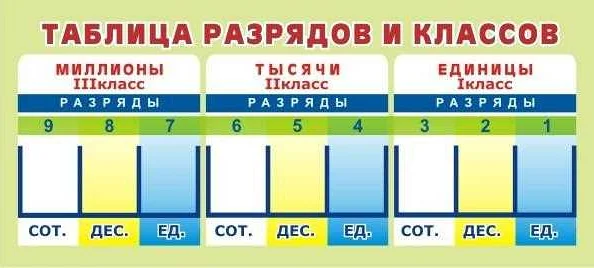
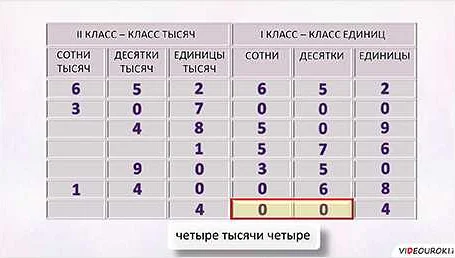
Классы — это группы разрядов, в которых записываются числа. Всего в десятичной системе счисления существует пять классов: сотни, тысячи, миллионы, миллиарды и триллионы. Каждый класс имеет свою особенность и значение. Например, разряды в классе «сотни» обозначают сотни, тысячи — тысячи, и так далее.

Разряды — это позиции чисел внутри каждого класса. В десятичной системе счисления каждый разряд имеет свое значение, которое увеличивается в 10 раз с каждым следующим разрядом. Например, в числе 542, разряд «единиц» равен 2, разряд «десятков» равен 4, а разряд «сотен» равен 5. Разряды позволяют нам определить порядок и значение каждой цифры в числе.

Например, число 3 456 789 можно разделить на классы и разряды следующим образом: класс «миллионы» (3), класс «тысячи» (456) и класс «единицы» (789).

Изучение классов и разрядов помогает нам лучше понять числа и их структуру. Это важные понятия, которые используются не только в математике, но и в повседневной жизни. Знание классов и разрядов поможет нам легче читать и записывать числа, а также проводить различные операции с ними.

Определение класса в математике

В математике, класс представляет собой группу объектов, обладающих общими характеристиками или свойствами. Классы используются для организации и классификации объектов в математической теории и в реальном мире.

Классы в математике могут быть определены по разным критериям, таким как форма, размер, свойства и отношения объектов. Например, классы могут быть определены для всех треугольников, кругов, прямоугольников и т. д., а также для всех чисел, которые являются кратными двум или трём.

Определение класса в математике помогает нам лучше понять свойства и отношения объектов и использовать их в решении математических задач. Знание классов позволяет нам проводить анализ и делать выводы о группе объектов на основе их общих характеристик.

Пример:

Рассмотрим класс «четные числа». В этом классе содержатся все числа, которые делятся на 2 без остатка. Например, числа 2, 4, 6, 8 и т. д. являются четными числами и относятся к данному классу. Этот класс можно использовать для решения задач, связанных с четными числами, например, для нахождения суммы, разности или произведения двух четных чисел.

В заключение, классы в математике играют важную роль в организации и систематизации объектов и их свойств. Они помогают нам лучше понять и использовать математические концепции и решать задачи.

Основные классы чисел

В математике существуют различные классы чисел, каждый из которых имеет свои особенности и свойства. Рассмотрим основные классы чисел:

1. Натуральные числа — это числа, которые используются для подсчета предметов, людей и т.д. Они обозначаются символами N или ℕ и включают в себя числа от 1 до бесконечности.
2. Целые числа — это числа, которые включают в себя натуральные числа и их отрицания, а также ноль. Они обозначаются символами Z или ℤ.
3. Рациональные числа — это числа, которые могут быть представлены в виде обыкновенной или десятичной дроби. Они обозначаются символами Q или ℚ.
4. Иррациональные числа — это числа, которые не могут быть представлены в виде обыкновенной или десятичной дроби. Они обозначаются символами I или ℍ.
5. Вещественные числа — это числа, которые включают в себя как рациональные, так и иррациональные числа. Они обозначаются символами R или ℝ.

Знание и понимание этих основных классов чисел является важной основой для изучения дальнейших математических тем и задач.

Натуральные числа и их свойства

Основные свойства натуральных чисел:

1. Порядковое свойство: Натуральные числа упорядочены по возрастанию. Число 2 следует за числом 1, число 3 следует за числом 2 и так далее.

2. Делимость: Натуральное число а делится на натуральное число b без остатка, если при делении числа а на число b получается целое число.

3. Непрерывность: Между любыми двумя натуральными числами всегда можно найти следующее число. Например, между числами 2 и 3 находится число 2,5.

4. Упорядоченность: Если два числа a и b являются натуральными числами и a меньше b, то a ближе к нулю, чем b.

5. Единственность нуля: Натуральные числа не содержат нуля. Ноль принадлежит к классу натуральных чисел.

Натуральные числа являются основой для изучения других классов чисел и используются во многих областях математики и науки.

Целые числа и их примеры

Целые числа образуют множество чисел, которые включают в себя натуральные числа, их противоположности (отрицательные числа) и ноль. Целые числа записываются без дробной части и могут быть положительными или отрицательными.

Примеры целых чисел:

• 3
• -5
• 0
• 10
• -2

Целые числа могут использоваться для представления различных ситуаций в реальном мире, таких как количество предметов, температура, долги и т.д. Они также играют важную роль в математических операциях, таких как сложение, вычитание, умножение и деление.

Рациональные числа и их характеристики

Рациональные числа можно представить как отношение двух целых чисел. Например, 1/2, 3/4, -5/7 являются рациональными числами.

Основные характеристики рациональных чисел:

1. Числитель и знаменатель — числитель и знаменатель обыкновенной дроби являются целыми числами. Числитель обозначает количество частей, которые нужно взять, а знаменатель — количество равных частей, на которые нужно поделить целое число.

Например, в дроби 2/5, числитель равен 2, а знаменатель равен 5.

2. Приближенное представление — рациональные числа могут быть представлены приближенно в виде десятичных дробей. Некоторые рациональные числа, такие как 1/3 или 2/7, имеют бесконечное количество десятичных знаков и не могут быть точно представлены. В таких случаях, числа округляются или записываются с ограниченным числом знаков после запятой.

3. Отношение и сравнение — рациональные числа могут быть сравнены друг с другом и установлено, какое из них больше или меньше. Например, 1/2 меньше 3/4, так как 1/2 является меньшей частью от целого числа, чем 3/4.

4. Арифметические операции — рациональные числа могут быть складываны, вычитаны, умножены и разделены друг на друга. При выполнении операций с рациональными числами результат также будет рациональным числом.

Рациональные числа являются важным понятием в математике и используются для решения широкого спектра задач, включая расчеты, моделирование и анализ данных.

Иррациональные числа и их особенности

Иррациональные числа, в свою очередь, не могут быть представлены как отношение двух целых чисел. Они представляют собой бесконечные и непериодические десятичные дроби.

Одним из самых известных иррациональных чисел является число π (пи). Оно равно отношению длины окружности к ее диаметру и приближенно равно 3,14159. Но на самом деле, число π не может быть точно выражено в виде десятичной дроби, так как оно имеет бесконечное количество десятичных знаков без периодической последовательности.

Еще одним примером иррационального числа является число √2 (корень из 2). Оно также не может быть точно выражено в виде десятичной дроби и приближенно равно 1,41421. Это число возникает из решения уравнения x^2 = 2, где x — не может быть представлено в виде рационального числа.

Иррациональные числа обладают рядом особенностей. Одна из особенностей заключается в том, что они не могут быть точно представлены в виде десятичных дробей и требуют бесконечного количества десятичных знаков для полного описания.

• Иррациональные числа не могут быть представлены в виде отношения двух целых чисел.
• Иррациональные числа имеют бесконечное количество десятичных знаков без периодической последовательности.
• Иррациональные числа могут возникать из решения некоторых уравнений.

Иррациональные числа играют важную роль в математике и имеют множество применений в различных областях науки. Изучение и понимание их особенностей помогает углубить знания в области математики и применять их в практических задачах.

Действительные числа и их представление

Действительные числа представляются на числовой прямой, где каждая точка соответствует определенному числу. Целые числа располагаются на числовой прямой с шагом 1, а десятичные дроби — с шагом меньше 1.

Действительные числа можно представить в виде десятичной дроби. Десятичная дробь состоит из целой части и десятичной части, разделенных запятой. Например, число 3,14 состоит из целой части 3 и десятичной части 0,14.

Еще одним способом представления действительных чисел является использование десятичных разрядов. Десятичные разряды показывают, сколько десятых, сотых, тысячных и так далее содержится в числе. Например, число 0,75 можно представить с помощью двух десятичных разрядов — 7,5 десятых.

Действительные числа имеют свойства сложения, вычитания, умножения и деления, которые позволяют выполнять различные операции с этими числами.

Знание действительных чисел и их представления является важным для понимания более сложных математических концепций и решения задач в различных областях.

Вопрос-ответ:

Какие классы и разряды есть в математике для 5 класса?

В математике для 5 класса есть классы чисел и разряды чисел. Классы чисел включают целые числа, натуральные числа, рациональные числа и иррациональные числа. Разряды чисел включают единицы, десятки, сотни, тысячи и т. д.

Какие основные понятия связаны с классами и разрядами в математике для 5 класса?

Основные понятия, связанные с классами и разрядами в математике для 5 класса, включают понятие класса чисел, понятие разряда числа, понятие позиционной системы счисления, понятие цифры, понятие числового значения и понятие порядка чисел.

Какие примеры можно привести для классов и разрядов в математике для 5 класса?

Примеры для классов чисел включают: целые числа (-3, -2, -1, 0, 1, 2, 3), натуральные числа (1, 2, 3, 4, 5), рациональные числа (1/2, 0.3, -0.25) и иррациональные числа (корень квадратный из 2, число π). Примеры для разрядов чисел включают: единицы (5, 7, 9), десятки (20, 30, 40), сотни (100, 200, 300), тысячи (1000, 2000, 3000).

Как понять позиционную систему счисления в математике для 5 класса?

Позиционная система счисления — это система, в которой значение числа зависит от позиции цифр в числе. В математике для 5 класса позиционная система счисления основана на десятичной системе, где каждая позиция числа имеет свой вес, например, в числе 235, 2 находится в разряде сотен, 3 — в разряде десятков и 5 — в разряде единиц.

Что такое порядок чисел в математике для 5 класса?

Порядок чисел — это способ сравнения чисел по их величине. В математике для 5 класса порядок чисел определяется с помощью знаков «» (больше) и «=» (равно). Например, число 10 больше числа 5, поэтому 10 > 5.

Что такое классы и разряды в математике?

Классы и разряды в математике — это способ организации чисел по разрядам, на основе позиции цифры в числе. Класс — это группа цифр, находящихся на одной позиции в числе, а разряд — это позиция цифры в числе.

Какие бывают классы и разряды в математике?

В математике есть классы и разряды для целых чисел, десятичных дробей и обыкновенных дробей. Для целых чисел классы и разряды определяются в зависимости от позиции цифры в числе. Для десятичных дробей классы и разряды определяются после запятой, а для обыкновенных дробей — до и после черты дроби.

Примеры задач на классы и разряды чисел

Пример 1:

Разложите число 356 на классы и разряды.

Решение:

Число 356 можно разложить на классы и разряды следующим образом:

В единицах: 6

В десятках: 5

В сотнях: 3

Пример 2:

Запишите число двести пятьдесят шесть в цифровой форме.

Решение:

Число двести пятьдесят шесть можно записать в цифровой форме следующим образом: 256.

Пример 3:

Определите разряды числа 9087.

Решение:

Число 9087 состоит из следующих разрядов:

Тысячи: 9

Сотни: 0

Десятки: 8

Единицы: 7

Пример 4:

Найдите сумму разрядов числа 5432.

Решение:

Сумма разрядов числа 5432 равна: 5 + 4 + 3 + 2 = 14.

Пример 5:

Определите классы числа 1298.

Решение:

Число 1298 состоит из следующих классов:

Тысячи: 1

Сотни: 2

Десятки: 9

Единицы: 8

Видео по теме: