Когда минус меняется на плюс в математике

Узнайте, когда и почему минус может превратиться в плюс в математике. Объяснение с примерами и правилами преобразования минуса в плюс.

Математика является одной из фундаментальных наук, которая изучает базовые законы и принципы чисел и операций. Одним из ключевых понятий в математике является отрицательное число, которое обозначает отсутствие или долг в определенной величине или величинах.

Однако существует способ преобразования отрицательных чисел в положительные. Этот процесс называется сменой знака и очень важен для решения различных математических задач. Смена знака позволяет преобразовать минус в плюс и наоборот, что дает возможность упростить вычисления и решать задачи более эффективно.

Чтобы сменить знак отрицательного числа, достаточно поставить перед ним знак «минус». Например, число -5 можно преобразовать в число 5, просто поставив перед ним знак «минус». Таким образом, операции с отрицательными числами становятся более простыми и понятными.

Преобразование отрицательных чисел в положительные имеет широкое применение в различных областях математики, физики и экономики. Оно помогает решать сложные задачи и упрощает вычисления. Понимание этого процесса позволяет лучше понять основные законы математики и использовать их для решения реальных проблем.

Таким образом, преобразование отрицательных чисел в положительные является важным инструментом в математике. Оно позволяет сделать операции с числами более простыми и понятными, а также находит применение в различных областях науки и экономики. Понимание этого процесса помогает лучше овладеть основами математики и применять их на практике.

Значение отрицательных чисел в математике

Отрицательные числа можно представить на числовой прямой, где положительные числа расположены справа от нуля, а отрицательные — слева. Ноль является точкой пересечения между положительными и отрицательными числами.

Отрицательные числа используются в различных областях математики, таких как алгебра, геометрия, физика и экономика. В алгебре они используются для решения уравнений и неравенств, в геометрии — для обозначения отрицательных координат или расстояний, в физике — для описания движения тела в противоположном направлении, а в экономике — для обозначения убытков или долгов.

Отрицательные числа можно складывать, вычитать, умножать и делить, применяя правила алгебры. Например, при сложении положительного числа и отрицательного числа результат будет отрицательным, при вычитании — положительным. Умножение двух отрицательных чисел даст положительный результат, а деление отрицательного числа на положительное — отрицательный результат.

Преобразование отрицательных чисел в плюсовые числа может быть полезным в некоторых случаях. Например, при решении уравнений или неравенств, иногда необходимо преобразовать выражение с отрицательными числами, чтобы упростить вычисления или найти корень уравнения.

ОперацияПримерРезультат

Сложение	-3 + 5	2
Вычитание	7 — (-2)	9
Умножение	-4 * (-3)	12
Деление	-6 / 2	-3

В заключение, отрицательные числа имеют свое значение в математике и играют важную роль в решении различных задач. Понимание и использование отрицательных чисел помогает в построении сложных моделей и решении сложных уравнений, а также в повседневных ситуациях, где нужно учитывать обратные значения или отсутствие чего-либо.

Отрицательные числа в реальной жизни

Финансы: Отрицательные числа широко используются в финансовой сфере. Например, если у вас есть задолженность по кредиту или на банковском счете отрицательный баланс, то это отражается отрицательным числом на вашем выписке. Отрицательные числа также используются для отображения убытков или долгов компаний.

Температура: Отрицательные числа применяются для измерения температуры. В холодные зимние дни термометр может показывать отрицательные значения, что указывает на низкую температуру окружающей среды.

Координаты: Отрицательные числа используются в географии и навигации. Координаты на плоскости, например, могут быть отрицательными, чтобы указывать положение на запад от нулевой точки. Также отрицательные числа применяются в географических широтах и долготах.

Время: Отрицательные числа могут использоваться для измерения времени. Например, если есть необходимость отсчитать время до или после определенного события, то отрицательные числа могут помочь представить это.

Математика: Отрицательные числа играют важную роль в математике. Они позволяют нам работать с относительными значениями и сравнивать числа в разных диапазонах. Отрицательные числа используются в алгебре, геометрии и других разделах математики.

Таким образом, отрицательные числа являются неотъемлемой частью нашей жизни, и их использование позволяет нам более точно описывать и понимать мир вокруг нас.

Математические операции с отрицательными числами

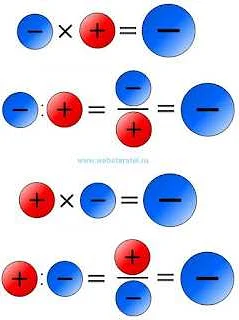
Сложение отрицательных чисел подобно сложению положительных чисел, только знак у результата будет отрицательным. Например, (-3) + (-5) = -8.

Вычитание отрицательных чисел также сводится к сложению. Например, (-3) — (-5) = (-3) + 5 = 2.

Умножение отрицательных чисел может привести как к положительному, так и к отрицательному результату. Умножение двух отрицательных чисел дает положительный результат. Например, (-2) * (-3) = 6. Умножение отрицательного числа на положительное дает отрицательный результат. Например, (-2) * 3 = -6.

Деление отрицательных чисел может также давать как положительный, так и отрицательный результат. Деление двух отрицательных чисел дает положительный результат. Например, (-6) / (-3) = 2. Деление отрицательного числа на положительное дает отрицательный результат. Например, (-6) / 3 = -2.

Устранение отрицательного знака в выражении может производиться с помощью скобок и применения правил арифметики. Например, -(-3) = 3. Это происходит из-за свойства двойного отрицания.

Знание основных математических операций с отрицательными числами позволяет работать с ними с уверенностью и правильно решать различные математические задачи.

Преобразование отрицательных чисел в положительные

В математике существует простой способ преобразования отрицательных чисел в положительные. Для этого нужно использовать знак минус, который стоит перед отрицательным числом, и поменять его на знак плюс. Таким образом, минус становится плюсом и отрицательное число превращается в положительное.

Например, если у нас есть число -5, то после преобразования оно станет числом +5. Аналогично, число -10 станет числом +10.

Преобразование отрицательных чисел в положительные может быть полезно во многих ситуациях. Например, при работе с выражениями и формулами, где требуется использование только положительных чисел. Также оно может быть полезно при работе с финансовыми показателями, где отрицательные значения могут иметь другое значение и требуют преобразования в положительные числа для дальнейшего анализа.

Важно понимать, что преобразование отрицательных чисел в положительные изменяет только знак числа. Его абсолютное значение остается неизменным. То есть, если у нас есть число -5, то после преобразования оно станет числом +5, но его абсолютное значение останется 5.

Преобразование отрицательных чисел в положительные является одной из основных операций в математике, которая дает возможность работать с отрицательными значениями и использовать их в различных контекстах. Знание этой операции позволяет уверенно выполнять математические вычисления и решать задачи, связанные с отрицательными числами.

Абсолютная величина отрицательного числа

Абсолютная величина отрицательного числа всегда является положительным числом. Например, абсолютная величина от -5 равна 5. Это связано с тем, что абсолютная величина представляет расстояние, которое всегда положительно.

Для вычисления абсолютной величины отрицательного числа достаточно убрать знак минус и взять число по модулю. Модуль числа — это абсолютное значение числа, то есть его значение без учета знака.

Например, абсолютная величина от -7 равна 7, так как убрав знак минус и взяв число по модулю, получаем 7.

Абсолютная величина отрицательного числа широко используется в различных областях математики и физики. Она позволяет избежать проблем с работой с отрицательными значениями и упростить вычисления.

Примеры преобразования отрицательных чисел

Преобразование отрицательных чисел в математике может привести к интересным результатам. Ниже приведены некоторые примеры:

1. Преобразование отрицательного числа в положительное:

Если у нас есть число -5 и мы преобразуем его в положительное число, то получим 5. Это можно сделать, поменяв знак числа на противоположный.

2. Преобразование отрицательного числа в десятичную дробь:

Чтобы преобразовать отрицательное число в десятичную дробь, мы можем применить правило десятичного разделителя. Например, если у нас есть число -3, то мы можем представить его в виде -3.0 или -3.00, где десятичная точка находится после нуля(или после нескольких нулей).

3. Преобразование отрицательного числа в процент:

Чтобы преобразовать отрицательное число в процент, мы можем представить его в виде отрицательного числа с символом процента. Например, если у нас есть число -10 и мы хотим представить его в процентах, мы можем написать -10%.

4. Преобразование отрицательного числа в дробь:

Отрицательное число можно преобразовать в дробь, представив его в виде отрицательного числителя и положительного знаменателя. Например, если у нас есть число -2, то мы можем представить его в виде -2/1.

Таким образом, преобразование отрицательных чисел может быть полезным при выполнении различных математических операций и представлении чисел в разных форматах.

Отрицательные числа и координатная плоскость

Координатная плоскость в математике представляет собой двумерную систему координат, состоящую из горизонтальной оси, называемой осью абсцисс, и вертикальной оси, называемой осью ординат. Оси пересекаются в точке, называемой началом координат, которая имеет координаты (0,0).

На координатной плоскости отрицательные числа представляются на оси абсцисс слева от начала координат. Так, число -1 находится на расстоянии одной единицы слева от начала координат. Чем дальше от начала координат, тем меньше значение числа. Например, число -2 находится на расстоянии двух единиц слева от начала координат.

На координатной плоскости отрицательные числа также могут быть представлены как точки. Каждому отрицательному числу соответствует точка, которая находится на оси абсцисс слева от начала координат. Например, точка (-1, 0) представляет число -1, а точка (-2, 0) представляет число -2.

Отрицательные числа на координатной плоскости также могут быть использованы для представления движения влево. Если положительные числа на координатной плоскости представляют движение вправо, то отрицательные числа представляют движение влево. Например, если точка A имеет координаты (2, 0), то движение на -1 единицу влево приведет нас к точке с координатами (1, 0).

Таким образом, отрицательные числа и координатная плоскость тесно связаны друг с другом. Они позволяют нам представлять и работать с отрицательными значениями, а также использовать их для представления движения влево на координатной плоскости.

Отрицательные числа в различных областях науки и техники

Отрицательные числа широко применяются в различных областях науки и техники для описания и моделирования различных явлений и процессов. Ниже приведены некоторые примеры использования отрицательных чисел в различных областях:

ОбластьПримеры использования отрицательных чисел

Математика	Отрицательные числа используются для обозначения долгов, убытков, отрицательных координат на координатной плоскости и других математических концепций.
Физика	Отрицательные числа используются для представления направления движения, напряжения, температуры и других физических величин.
Экономика	Отрицательные числа используются для обозначения убытков, долгов, отрицательных изменений в экономических показателях.
Инженерия	Отрицательные числа используются для моделирования отрицательных значений мощности, силы, давления и других параметров в инженерных расчетах.

Отрицательные числа играют важную роль в разных областях науки и техники, позволяя более точно описывать и анализировать различные явления и процессы. Их использование позволяет ученным и инженерам более полно и точно описывать и предсказывать различные явления и процессы в реальном мире.

Вопрос-ответ:

Что такое отрицательные числа в математике?

Отрицательные числа — это числа, которые меньше нуля. Они обозначаются символом «минус» перед числом, например, -3.

Как можно преобразовать отрицательное число в положительное?

Отрицательное число можно преобразовать в положительное, поменяв знак числа на противоположный. Например, отрицательное число -5 можно преобразовать в положительное, изменив знак на плюс и получив 5.

Какое правило существует для сложения отрицательных чисел?

Правило сложения отрицательных чисел гласит, что если складываются два отрицательных числа, то результат будет отрицательным числом со знаком минус. Например, -2 + (-3) = -5.

Какое правило существует для умножения отрицательных чисел?

Правило умножения отрицательных чисел гласит, что если умножаются два отрицательных числа, то результат будет положительным числом. Например, (-2) * (-3) = 6.

Может ли отрицательное число быть больше, чем положительное число?

Да, отрицательное число может быть больше по модулю, чем положительное число. Например, -5 больше по модулю, чем 3. Однако, если сравнивать числа по значению, то положительное число всегда будет больше отрицательного.

Какое значение имеют отрицательные числа в математике?

В математике отрицательные числа используются для обозначения долгов, убытков, отрицательных значений и других ситуаций, когда необходимо указать отрицательное значение.

Видео по теме: