Что такое минус в математике

Математическое понятие минуса представляет собой операцию вычитания, которая используется для отрицания числа или для вычисления разности между двумя числами. Узнайте, как минус работает в математике и как его использовать для решения задач.

Минус — это одна из основных операций в математике, которая обозначает вычитание одного числа из другого. Если операция сложения объединяет два числа и дает сумму, то минус выполняет обратную операцию — разность.

Знак минуса (-) используется не только для обозначения операции вычитания, но и для других математических операций, например, для обозначения отрицательных чисел. Если число отрицательно, перед ним ставится знак минуса, который указывает на недостаток или отсутствие чего-либо.

Минус также применяется для обозначения отрицательных результатов и величин. Например, если температура находится ниже нуля, перед её значением ставится знак минуса.

Использование знака минуса в математике важно для правильного представления и понимания различных числовых операций и концепций. Без него было бы сложнее выражать отрицательные значения и результаты вычитания.

Историческое происхождение минуса

Первые упоминания о знаке минуса встречаются в работах арабских математиков IX-X веков. Они использовали знаки плюса (+) и минуса (-) для обозначения сложения и вычитания. Однако, эти символы использовались не в том виде, в котором мы знаем их сейчас.

Наиболее близкое к современному виду знака минуса описание было найдено в работах Иоганна Бернулли и Леонарда Эйлера в XVIII веке. Они предложили использовать горизонтальную черту для обозначения отрицательных чисел и вычитания. Этот символ стал широко распространенным и использовался во многих странах.

В конце XIX века нашел свое применение и более современный знак минуса, который мы используем сегодня. Он был введен для единообразия записи и был предложен Питером Густавом Лебецом. Горизонтальная черта заменилась вертикальной чертой, чтобы минус легко отличался от плюса.

С течением времени знак минуса стал неотъемлемой частью математической нотации. Он используется для обозначения отрицательных чисел, вычитания, а также в других областях математики и физики.

Определение и значение минуса

Значение минуса заключается в том, что он показывает разность между двумя числами или вычитаемым и их разностью. Минус используется для вычитания одного числа из другого и указывает, насколько одно число меньше другого.

Например, если у нас есть числа 10 и 5, мы можем записать их разность с помощью минуса: 10 — 5 = 5. Здесь минус указывает, что разность между 10 и 5 равна 5.

Минус также может использоваться для отрицательных чисел. Например, -5 означает, что число 5 отрицательное и меньше нуля.

Операция вычитания с использованием минуса широко применяется в математике, физике, экономике и других науках. Она позволяет находить разности между числами и измерять изменения величин.

Математические операции с использованием минуса

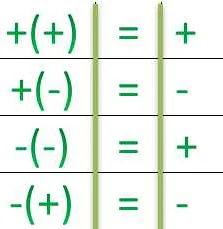
Например, если у нас есть числа 5 и 3, мы можем вычесть 3 из 5, записав это как 5 — 3 = 2. В этом случае минус указывает на операцию вычитания и показывает, что результатом будет число 2.

Минус также может использоваться для обозначения отрицательных чисел. Если перед числом стоит знак «-«, это означает, что число отрицательное.

Например, если у нас есть число -4, это означает, что число 4 отрицательное. Такое обозначение помогает отличать отрицательные числа от положительных и выполнять с ними соответствующие математические операции.

Операции с использованием минуса можно выполнять не только с целыми числами, но и с десятичными числами, дробями и другими математическими выражениями. Все это позволяет решать разнообразные задачи и получать точные результаты.

ПримерОперацияРезультат

10 — 5	Вычитание	5
3 — 7	Вычитание	-4
2.5 — 1.3	Вычитание	1.2
3/4 — 1/2	Вычитание	1/4

Таким образом, минус является важным математическим символом, который позволяет выполнять операции вычитания и обозначать отрицательные числа. Знание и использование минуса необходимо для решения различных математических задач и получения точных результатов.

Применение минуса в арифметике

Минус может использоваться для выполнения следующих действий:

• Вычитание: минус позволяет вычитать одно число из другого. Например, 10 — 5 = 5.
• Обратное число: минус перед числом позволяет получить его обратное значение. Например, -5 обратное -(-5).
• Операции с отрицательными числами: минус позволяет выполнять операции с отрицательными числами, такие как сложение, умножение и деление.

Применение минуса в арифметике не ограничивается только вычитанием. Он также может использоваться в комбинации с другими операторами, такими как плюс (+), умножение (*) и деление (/), для выполнения сложных математических выражений.

Важно помнить, что порядок применения операторов в выражении также имеет значение. Использование скобок может помочь установить порядок операций и избежать ошибок при вычислении.

В заключение, минус имеет широкий спектр применений в арифметике и позволяет выполнять различные математические операции. Понимание его значения и использование может быть полезным в решении задач и проведении вычислений.

Роль минуса в алгебре

Минус в алгебре играет важную роль и имеет несколько различных значений и использований. Во-первых, он используется для обозначения отрицательных чисел. Когда мы сталкиваемся с отрицательными значениями, мы можем использовать знак минуса, чтобы указать, что число меньше нуля.

Кроме того, минус используется для обозначения разности или вычитания. В алгебре мы можем вычитать одно число из другого, чтобы получить разность. Знак минуса показывает, что одно значение вычитается из другого.

Также минус может использоваться для обозначения противоположного числа. Если у нас есть число, мы можем найти его противоположное значение, поместив перед ним знак минуса. Например, если у нас есть число 5, его противоположное значение будет -5.

Кроме того, минус может быть использован для обозначения отрицания в алгебре. Например, если мы имеем выражение «не А», мы можем использовать знак минуса, чтобы обозначить отрицание А.

Таким образом, минус в алгебре играет важную роль, позволяя нам работать с отрицательными числами, вычитать значения, находить противоположные числа и обозначать отрицание.

Работа с отрицательными числами и минусом

Отрицательные числа играют важную роль в математике и имеют свои особенности. В основе отрицательных чисел лежит понятие минуса.

Минус — это знак, который используется для обозначения отрицательных чисел. Он ставится перед числом и указывает на то, что это число меньше нуля. Например, -5, -2, -10 — это отрицательные числа.

Работа с отрицательными числами включает в себя выполнение различных операций, таких как сложение, вычитание, умножение и деление.

• Сложение отрицательных чисел. Если складывать два отрицательных числа, то получится отрицательная сумма. Например, (-5) + (-3) = -8.
• Вычитание отрицательных чисел. Вычитание отрицательного числа эквивалентно сложению положительного числа. Например, 5 — (-3) = 5 + 3 = 8.
• Умножение отрицательных чисел. Умножение двух отрицательных чисел дает положительный результат. Например, (-5) * (-3) = 15.
• Деление отрицательных чисел. Деление двух отрицательных чисел также дает положительный результат. Например, (-9) / (-3) = 3.

Работа с отрицательными числами в математике также связана с понятием абсолютной величины числа. Абсолютная величина числа — это число без знака минус. Например, абсолютная величина числа -5 равна 5.

Понимание работы с отрицательными числами и минусом является важным элементом в основах математики и может быть полезно в решении различных задач и проблем.

Вопрос-ответ:

В чем заключается значение минуса в математике?

Минус в математике является знаком операции вычитания и обозначает отрицание числа или значения. Он позволяет выполнить операцию вычитания и указать, что одно число следует вычесть из другого.

Как использовать минус в математике?

Минус используется в математике для выполнения операции вычитания. Если у вас есть два числа, вы можете поставить минус между ними и выполнить вычитание первого числа из второго. Например, 8 — 3 = 5. Также минус может использоваться для обозначения отрицательных чисел, например, -5.

Какие еще значения может иметь минус в математике?

В математике минус может использоваться для обозначения различных вещей. Он может обозначать отрицательные числа, например, -5. Также минус может использоваться для обозначения отрицания или противоположности, например, -x означает противоположное значение переменной x. Минус может также использоваться в алгебре для обозначения отрицательных степеней, например, x^-2 означает обратное значение x в квадрате.

Как можно объяснить значение минуса детям?

Минус в математике можно объяснить детям как знак, который говорит нам, что одно число следует вычесть из другого. Например, если у нас есть 7 яблок и мы съедаем 3 яблока, мы можем записать это как 7 — 3 = 4. Также можно объяснить детям, что минус может означать отрицательные числа или противоположность. Например, если у нас есть 5 долларов, а мы потратили 7 долларов, мы можем записать это как -7.

Решение уравнений с использованием минуса

При решении уравнений с использованием минуса основной принцип заключается в переносе одного члена уравнения на другую сторону с изменением знака. Таким образом, при переносе члена с положительным знаком на другую сторону уравнения он становится отрицательным, а при переносе члена с отрицательным знаком он становится положительным.

Например, рассмотрим уравнение:

3x — 5 = 10

Для начала, перенесем член с отрицательным знаком на другую сторону уравнения:

3x = 10 + 5

Далее, выполнив операцию сложения, получим:

3x = 15

И наконец, разделив обе части уравнения на коэффициент при неизвестной переменной, найдем значение x:

x = 15/3

Ответ: x = 5

Таким образом, использование минуса позволяет решать различные уравнения и находить значения неизвестных переменных.

Видео по теме: