Когда изучают пределы в математике

Изучение пределов в математике происходит на разных этапах обучения, начиная с школьного курса и продолжая в университете. Пределы являются важным понятием для понимания и анализа функций, а также для решения различных задач в математике и ее приложениях. Узнайте, как и когда студенты изучают пределы и почему это так важно для их математического развития.

Изучение пределов является важной частью курса математики и охватывает различные аспекты, которые позволяют понять и применять основные понятия этой области знаний. Но когда именно начинают изучать пределы в математике?

Обычно, изучение пределов начинается в учебных заведениях на старших классах средней школы или в университете на первом курсе. Перед началом изучения пределов студенты должны иметь базовые знания в области алгебры и геометрии, такие как арифметические операции, уравнения и графики. Это поможет им лучше понять и применять понятия пределов в математике.

Изучение пределов в математике позволяет анализировать поведение функций при приближении аргумента к определенной точке. Пределы позволяют определить, как функция ведет себя вблизи данной точки и как можно приблизиться к этой точке. Это полезное понятие применяется в различных областях, включая физику, экономику и компьютерные науки.

Изучение пределов является важным шагом в развитии математической интуиции и абстрактного мышления. Понятие предела позволяет увидеть связь между аналитическими и геометрическими свойствами функций, а также позволяет решать сложные задачи, которые требуют аппроксимации и приближений.

В целом, изучение пределов в математике является важным этапом в углубленном изучении этой науки и открывает двери к более сложным математическим концепциям и теориям. Понимание основных моментов, связанных с пределами, позволяет развить логическое мышление и умение анализировать сложные математические проблемы.

Что такое пределы в математике?

Формально, предел функции f(x) при x, стремящемся к a, можно определить следующим образом: если для любого положительного числа ε существует положительное число δ, такое что для всех x, таких что 0 < |x — a| < δ, выполняется |f(x) — L| < ε, то говорят, что предел функции f(x) равен L при x, стремящемся к a, и записывается как lim(x→a) f(x) = L. Здесь L — предельное значение функции, a — точка приближения, ε и δ — произвольные положительные числа.

Пределы позволяют изучать поведение функций и последовательностей в окрестности определенной точки. Они находят широкое применение в различных областях математики, физики, экономики и других наук, где требуется анализ изменения величин при приближении к определенным значениям.

Видео по теме:

Почему пределы важны в математике?

Одним из основных применений пределов является нахождение значений функций в точках, где они не определены. Пределы позволяют нам приближаться к таким точкам и определять их значение, что важно, например, при решении уравнений и задач физики, где функции могут иметь разрывы или особые точки.

Пределы также играют важную роль при изучении производных и интегралов. Они позволяют определить скорость изменения функции в каждой ее точке и вычислить площадь под графиком функции, что необходимо для решения многих задач, связанных с оптимизацией и моделированием.

Пределы также широко используются в анализе функций и последовательностей. Они позволяют определить, сходится ли последовательность к определенному значению или бесконечно приближается к нему. Это важно при изучении сходимости рядов, суммировании бесконечных последовательностей и других математических операциях.

Кроме того, пределы позволяют анализировать границы и ограничения функций. Они помогают определить, при каких значениях переменных функция стремится к бесконечности или имеет особое поведение. Это полезно для понимания асимптотического поведения функций и решения задач, связанных с ограничениями и условиями.

Применение пределов в математике:

Нахождение значений функций в неопределенных точках

Вычисление производных и интегралов

Анализ сходимости функций и последовательностей

Определение границ и ограничений функций

Какие основные понятия связаны с пределами?

Изучение пределов в математике включает в себя несколько важных понятий, которые помогают понять, как функция ведет себя в окрестности определенной точки.

Предел функции — это значение, к которому функция стремится, когда аргумент приближается к определенной точке. Предел функции может быть как конечным числом, так и бесконечностью.

Бесконечно малая — это функция, которая стремится к нулю, когда аргумент стремится к определенной точке. Бесконечно малые часто используются для определения пределов функций.

Бесконечно большая — это функция, которая стремится к бесконечности, когда аргумент приближается к определенной точке. Бесконечно большие также используются для определения пределов функций.

Ограниченность функции — это свойство функции, когда она не выходит за определенные границы. Функция может быть ограниченной сверху, снизу или с обеих сторон.

Непрерывность функции — это свойство функции, когда она не имеет разрывов и может быть нарисована без поднятия карандаша. Функция является непрерывной на интервале, если она непрерывна в каждой точке этого интервала.

Производная функции — это показатель изменения функции в зависимости от аргумента. Производная функции позволяет определить ее скорость роста или падения в каждой точке.

Понимание этих понятий помогает более глубоко изучить пределы функций и их свойства, а также проводить анализ математических моделей и решать задачи различных областей науки и техники.

Вопрос-ответ:

Когда начинают изучать пределы в математике?

Изучение пределов в математике начинается в средней школе, обычно в 10-11 классе. Это одна из важных тем в курсе математики и представляет собой основу для дальнейшего изучения математического анализа.

Какие основные моменты нужно знать о пределах?

Основные моменты, которые нужно знать о пределах, включают определение предела функции, связанные с ним понятия бесконечно малых и бесконечно больших, основные свойства пределов, а также методы вычисления пределов.

Зачем изучать пределы в математике?

Изучение пределов в математике позволяет понять и описать поведение функций в окрестности определенной точки. Это является основой для анализа функций, определения их экстремумов, построения графиков функций и решения многих задач в различных областях науки и техники.

Какие методы вычисления пределов существуют?

Существует несколько методов вычисления пределов, включая методы подстановки, использования основных свойств пределов, правило Лопиталя, разложение в ряд и др. Каждый метод применяется в зависимости от конкретной задачи и условий функции.

Могу ли я понять предел функции без математического анализа?

Некоторые пределы функций можно понять и описать без использования математического анализа. Например, если функция имеет асимптоту или явные границы в окрестности точки, то можно сделать предположение о пределе. Однако для точного вычисления пределов и решения сложных задач требуется знание математического анализа.

Когда начинают изучать пределы в математике?

Изучение пределов в математике начинается обычно в средней школе, в рамках курса алгебры. Это обычно происходит в 9-10 классе.

Какие основные моменты нужно знать о пределах в математике?

Основные моменты, которые нужно знать о пределах в математике, включают понятие предела функции, его свойства, методы нахождения предела и взаимосвязь пределов и непрерывности функций.

Какое значение имеет понятие предела в анализе функций?

Математически, предел функции определяется как значение, к которому стремится функция при приближении аргумента к определенной точке. Если функция имеет предел в данной точке, то она непрерывна в этой точке и может быть разложена в ряд Тейлора.

Понятие предела важно для понимания основных свойств функций и их графиков. Оно позволяет определить, например, вертикальные и горизонтальные асимптоты функции, точки разрыва и устремление функции к определенным значениям на бесконечности.

Также понятие предела широко применяется в решении математических задач, в физике, экономике и других науках. Например, в физике пределы используются для описания движения тела, изменения температуры и других физических величин.

Итак, понятие предела имеет фундаментальное значение в анализе функций. Оно позволяет понять и описать поведение функции вблизи определенной точки и используется в широком спектре наук и приложений.

Какова роль пределов в теории вероятностей и статистике?

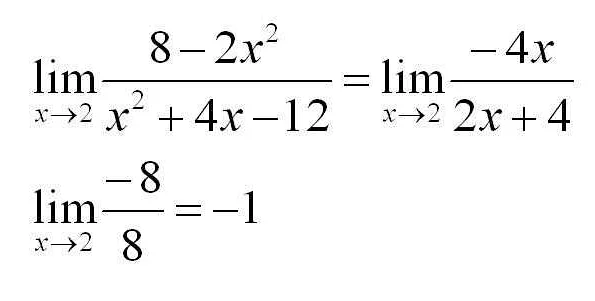
Пределы играют важную роль в теории вероятностей и статистике, позволяя анализировать случайные явления и оценивать вероятности различных событий.

В теории вероятностей, пределы используются для описания поведения случайных величин при увеличении числа экспериментов. Например, закон больших чисел основан на предельных свойствах случайных величин. Он утверждает, что среднее значение последовательности случайных величин, взятых из одного и того же распределения, сходится к математическому ожиданию этого распределения при увеличении числа экспериментов.

В статистике пределы используются для оценки параметров распределений на основе выборочных данных. Например, при оценке среднего значения выборки пределы позволяют определить доверительный интервал, в котором находится истинное среднее значение с заданной вероятностью. Также пределы используются для проверки гипотез о параметрах распределений.

Пределы также играют важную роль в анализе временных рядов и последовательностей случайных величин. Например, предельные значения автокорреляционной функции могут быть использованы для определения наличия стационарности во временном ряде.

Таким образом, понимание и использование пределов является неотъемлемой частью теории вероятностей и статистики, позволяя проводить анализ, делать выводы и принимать решения на основе случайных данных.

Как начинают изучать пределы в школьной программе?

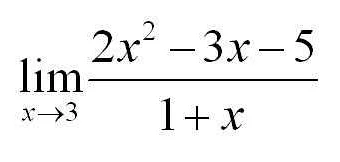
Изучение пределов в математике начинается в старших классах школы. Обычно это происходит в 10-11 классах. Вначале ученики изучают понятие предела функции в точке. Они учатся находить пределы функций аналитическим методом, используя алгебраические преобразования и специальные приемы.

Затем ученики изучают понятие бесконечного предела. Они учатся определять, к чему стремится функция, если ее переменная стремится к бесконечности. Это позволяет рассматривать поведение функции на бесконечности.

Кроме того, в программе изучается понятие предела последовательности. Ученики учатся определять, к какому числу стремится последовательность, и находить пределы различных видов последовательностей.

Изучение пределов в школьной программе является важной частью математического образования. Понимание понятия предела и умение находить пределы функций и последовательностей являются ключевыми навыками в дальнейшем изучении математики и связанных с ней наук.

На каком уровне образования обычно начинают изучать пределы?

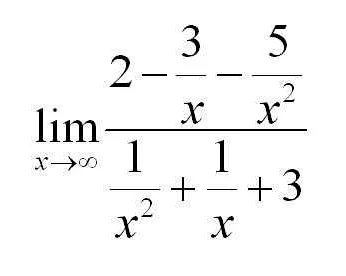
В школьной программе пределы обычно изучают в старших классах, в рамках курса математики или алгебры. Ученики узнают, как определить предел функции, как искать односторонние пределы, что такое бесконечно малая величина и бесконечно большая величина. Изучение пределов помогает ученикам понять, как работают функции и какие значения они могут принимать в разных точках.

В вузе изучение пределов проходит на более глубоком уровне, в рамках курса математического анализа. Студенты углубляются в теорию пределов, изучают основные свойства и правила, которые позволяют решать сложные математические задачи. Разделение на числитель и знаменатель, нахождение предела сложных функций, использование различных методов – все это является частью обучения пределам на уровне вуза.

Изучение пределов в математике является важным этапом в образовании и позволяет развить аналитическое мышление и навыки решения сложных математических задач. Студенты, которые хорошо усваивают материал по пределам, получают прочный фундамент для изучения более сложных математических концепций в будущем.

Какие умения и навыки развиваются при изучении пределов?

Изучение пределов в математике развивает ряд важных умений и навыков, которые могут быть полезными не только в самой математике, но и в других сферах жизни. Вот несколько основных умений и навыков, которые развиваются при изучении пределов:

1. Аналитическое мышление: Изучение пределов требует анализа и понимания сложных математических концепций и связей. Это способствует развитию аналитического мышления и способности к решению проблем.
2. Логическое мышление: При изучении пределов необходимо применять логические принципы для вывода результатов и решения математических задач. Это помогает развить навыки логического мышления и аргументации.
3. Точность и внимательность: В процессе работы с пределами необходимо быть очень внимательным и точным, чтобы не допустить ошибок в рассуждениях и вычислениях. Это способствует развитию навыков точности и внимательности в решении задач.
4. Абстрактное мышление: Изучение пределов требует способности мыслить абстрактно и работать с абстрактными понятиями. Это развивает способность видеть общие закономерности и применять их в различных контекстах.
5. Решение проблем: Изучение пределов помогает развить навыки поиска и применения различных методов и стратегий для решения сложных математических задач. Это развивает способность решать проблемы и находить креативные подходы к их решению.

Эти умения и навыки, развитые при изучении пределов, могут быть полезными не только в математике, но и в других научных и практических областях, где требуется аналитическое мышление, логика и точность.