Коэффициент в математике это что

Коэффициент в математике – это числовое значение, которое определяет отношение между двумя величинами. В математических уравнениях и формулах коэффициенты играют важную роль, позволяя устанавливать связи и зависимости между переменными. Различные типы коэффициентов используются в разных областях математики, таких как алгебра, геометрия, статистика и дифференциальные уравнения.

В математике коэффициент — это числовое значение, которое умножается на переменную или слагаемое. Он используется для выражения зависимости между различными величинами и является одной из основных концепций алгебры. Коэффициенты помогают нам изучать и понимать различные явления и взаимосвязи в мире чисел и формул.

Коэффициенты находят широкое применение в различных областях, включая физику, экономику, технику и т.д. Они позволяют нам анализировать и решать различные задачи, предсказывать и описывать различные явления. Например, в физике коэффициенты используются для описания законов движения тела или характеристик волновых процессов.

Примеры использования коэффициентов можно найти в различных математических формулах и уравнениях. Например, в уравнении прямой y = mx + b, где m — это коэффициент наклона прямой, а b — это коэффициент смещения по оси y. В алгебре коэффициенты могут также представлять собой числовые значения перед переменными в алгебраических выражениях или полиномах.

Использование коэффициентов позволяет нам более точно и полно описывать и изучать различные явления и процессы в математике и ее приложениях. Они помогают нам выявлять и анализировать взаимосвязи, создавать модели и предсказывать результаты. Понимание коэффициентов является важным элементом в освоении математических наук и развитии аналитического мышления.

Коэффициент в математике: основное понятие и значение

В алгебре и анализе коэффициенты часто используются при решении уравнений и систем уравнений. Например, в линейном уравнении y = mx + b, m является коэффициентом наклона прямой, определяющим ее угол наклона.

В физике коэффициенты также имеют важное значение. Например, в формуле закона Ома, сопротивление R является коэффициентом пропорциональности между напряжением V и силой тока I: V = IR.

В экономике коэффициенты используются для определения степени влияния различных факторов на экономические показатели. Например, коэффициент эластичности спроса показывает, насколько процентное изменение цены товара приведет к изменению его спроса.

Коэффициенты могут быть положительными, отрицательными или нулевыми, в зависимости от контекста и значения, которое они представляют. Они могут также быть дробными или целыми числами.

В заключение, коэффициенты являются важными инструментами для измерения и анализа относительных величин в математике, физике и экономике. Понимание и использование коэффициентов позволяет более точно описывать и предсказывать различные явления и процессы.

Видео по теме:

Что такое коэффициент в математике и как он определяется?

Определение коэффициента зависит от конкретной математической области. Например, в линейной алгебре коэффициент может быть использован для определения связи между координатами векторов или для решения систем линейных уравнений. В математическом анализе коэффициенты могут использоваться для нахождения производных или интегралов функций. В статистике коэффициенты могут служить для измерения степени корреляции между переменными.

Часто коэффициенты обозначаются буквами, такими как a, b, c и т.д. Они могут быть числами, обычно вещественными или комплексными. Коэффициенты также могут быть положительными, отрицательными или нулевыми, в зависимости от своей роли и значения в уравнении или формуле.

В общем случае, коэффициент – это важный математический инструмент, который позволяет анализировать и понимать различные математические зависимости и отношения между величинами. Он широко используется во многих разделах математики и науки в целом.

Значение коэффициента в различных математических областях

В алгебре коэффициент может использоваться для описания отношений между переменными или для определения веса или силы в уравнениях. Например, в линейном уравнении y = mx + b коэффициент m представляет собой скорость изменения и наклон прямой.

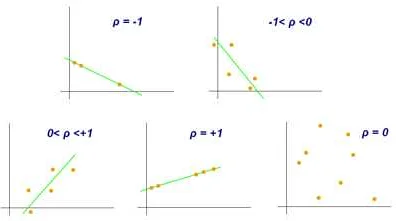
В статистике коэффициенты используются для изучения взаимосвязей между переменными. Например, корреляционный коэффициент измеряет силу и направление линейной связи между двумя переменными.

В физике коэффициенты могут использоваться для описания физических процессов и законов. Например, коэффициент трения определяет силу трения между двумя поверхностями, а коэффициент упругости характеризует способность материала возвращаться к своей исходной форме после деформации.

В экономике коэффициенты используются для измерения и анализа различных показателей, таких как рентабельность, эффективность, ликвидность и другие. Например, коэффициент ликвидности позволяет оценить способность предприятия преобразовать активы в денежные средства.

Коэффициенты также используются в других областях математики, таких как геометрия, теория вероятности, дифференциальные уравнения и многие другие. В каждой области значение и интерпретация коэффициентов могут отличаться, но общая идея о числовом множителе остается неизменной.

Вопрос-ответ:

Что такое коэффициент в математике?

Коэффициент в математике — это число, которое умножается на переменную или на другое число. Он используется для определения отношений, пропорций и связей между различными величинами.

Какие примеры использования коэффициента в математике?

В математике коэффициент может использоваться во множестве различных ситуаций. Например, в алгебре он используется для решения уравнений и систем уравнений. В геометрии коэффициент может определять угол наклона прямой. В физике коэффициент используется для описания законов и формул, таких как закон Ома или закон Гука.

Как определить значение коэффициента в математике?

Значение коэффициента может быть определено различными способами, в зависимости от контекста. Например, в алгебре значение коэффициента может быть найдено путем решения уравнения. В геометрии значение коэффициента может быть определено путем измерения угла наклона прямой. В физике значение коэффициента может быть определено путем экспериментальных измерений или расчетов.

Какие свойства имеет коэффициент в математике?

Коэффициент в математике может обладать различными свойствами в зависимости от контекста. Например, в алгебре коэффициент может быть положительным или отрицательным, вещественным или комплексным. В геометрии коэффициент может быть равен нулю, если прямая параллельна оси. В физике коэффициент может иметь единицы измерения и быть связан с физической величиной, такой как сопротивление или жесткость.

Какие примеры реального применения коэффициента в математике?

Коэффициент в математике широко используется в реальной жизни. Например, в экономике коэффициент используется для анализа роста или снижения цен, объема продаж или процента покупателей. В физике коэффициент используется для определения электрического сопротивления проводника или измерения жесткости пружины. В статистике коэффициент используется для описания связей между переменными, таких как корреляция или регрессия.

Как определить коэффициент в математике?

Коэффициент в математике — это число, на которое умножается другое число или переменная. Он используется для изменения масштаба, установки соответствующего соотношения или вычисления нового значения. Коэффициент может быть положительным, отрицательным или нулевым.

Коэффициент в алгебре и арифметике: примеры использования

Рассмотрим несколько примеров использования коэффициента:

1. Коэффициент при переменной в линейном уравнении:

Пусть дано уравнение: y = 2x + 3. Здесь коэффициент 2 указывает на то, что переменная x должна быть умножена на 2. Коэффициент 3 указывает на свободный член, который прибавляется к результату.

2. Коэффициент при переменной в квадратном уравнении:

Пусть дано уравнение: y = ax^2 + bx + c. Здесь коэффициент a указывает на то, что переменная x должна быть возводится в квадрат, а затем умножаться на a. Коэффициенты b и c определяют взаимосвязь переменных в уравнении.

3. Коэффициент в арифметической прогрессии:

Арифметическая прогрессия – это последовательность чисел, в которой каждое следующее число получается путем прибавления к предыдущему числу постоянного шага. В этой последовательности каждое число умножается на коэффициент, который определяет этот шаг. Например, в прогрессии 2, 5, 8, 11, 14 коэффициент равен 3, так как каждое следующее число получается путем добавления 3 к предыдущему.

Таким образом, коэффициент в алгебре и арифметике играет важную роль в определении зависимостей между переменными и в вычислениях.

Коэффициент в геометрии: применение и примеры

Один из наиболее распространенных примеров использования коэффициента в геометрии — это коэффициент подобия. Коэффициент подобия позволяет сравнить геометрические фигуры на предмет их сходства или различия. Он вычисляется путем сравнения соответствующих сторон или измерений фигур и показывает, насколько одна фигура подобна другой.

Например, если у нас есть два треугольника, и мы хотим определить, насколько они похожи, мы можем вычислить коэффициент подобия. Для этого мы сравниваем соответствующие стороны треугольников и делим их друг на друга. Если полученный результат близок к 1, это означает, что треугольники очень похожи, а если результат далек от 1, то они сильно отличаются.

Коэффициент в геометрии также используется для измерения других характеристик фигур, таких как площадь, объем, длина дуги и т. д. Например, коэффициент пропорциональности используется для определения отношения между площадью фигуры и ее линейными размерами. Он позволяет нам сравнивать изменение площади фигуры при изменении ее размеров.

Таким образом, коэффициент в геометрии является мощным инструментом, который позволяет измерять и сравнивать различные характеристики геометрических фигур. Он помогает нам понять и описать особенности и свойства этих фигур, а также использовать их для решения различных геометрических задач и задач из других областей.

Важность коэффициента в статистике и вероятности

Коэффициенты играют важную роль в статистике и вероятности, так как они позволяют оценивать и измерять различные явления и связи между ними.

В статистике коэффициенты используются для измерения степени взаимосвязи между различными переменными. Например, коэффициент корреляции позволяет определить, насколько две переменные связаны между собой. Это особенно полезно при исследовании зависимостей в больших объемах данных и при построении моделей прогнозирования.

Вероятностные коэффициенты играют важную роль при анализе случайных событий и расчете вероятностей. Например, коэффициент корреляции в вероятности позволяет оценить, насколько две случайные величины зависимы друг от друга. Также в статистике используются коэффициенты, которые помогают оценивать вероятности событий и принимать решения на основе этих вероятностей.

Использование коэффициентов в статистике и вероятности позволяет более объективно и точно анализировать данные и делать выводы о связях и вероятностях. Они помогают ученым и исследователям проводить более качественные исследования, а также предсказывать и прогнозировать различные явления и события.

Использование коэффициента в физике и химии

Коэффициенты широко используются в физике и химии для описания различных физических и химических явлений. Они позволяют установить математическую связь между различными величинами и сделать выводы о зависимостях между ними.

В физике, коэффициенты используются для описания различных физических законов и формул. Например, в законе Ома, сопротивление электрической цепи определяется коэффициентом пропорциональности между напряжением и током. Также коэффициенты используются в законе Гука для описания упругих деформаций материала.

В химии, коэффициенты используются, например, для балансировки химических реакций. Коэффициенты перед формулами химических веществ показывают, в каком соотношении они участвуют в реакции. Они позволяют соблюдать законы сохранения массы и энергии и сделать выводы о количестве веществ, участвующих в реакции.

Коэффициенты также используются для описания различных физических и химических свойств веществ. Например, коэффициенты теплопроводности, коэффициенты растворимости, коэффициенты поглощения света и т. д. Они позволяют описывать свойства веществ и делать выводы о их взаимодействии с окружающей средой.

Коэффициент в экономике: роль и примеры использования

Один из наиболее распространенных примеров использования коэффициентов в экономике — это коэффициент экономической активности. Этот коэффициент позволяет оценить долю экономически активного населения в общей численности населения страны. Такой коэффициент является важным индикатором для определения уровня занятости и развития рынка труда в стране.

Кроме того, в экономике используются и другие коэффициенты, например, коэффициент ликвидности. Данный коэффициент позволяет определить способность предприятия или организации к погашению текущих обязательств по долгам и кредитам. Коэффициент ликвидности является важным индикатором финансовой устойчивости и платежеспособности компании.

Еще одним примером использования коэффициента в экономике является коэффициент доходности инвестиций. Этот коэффициент позволяет определить эффективность инвестиций и их возвратность. По этому коэффициенту можно сделать выводы о том, насколько успешно использовались инвестиции для получения прибыли.

Название коэффициентаОписаниеПример использования

Коэффициент экономической активности	Определяет долю экономически активного населения	Оценка уровня занятости и развития рынка труда
Коэффициент ликвидности	Определяет способность к погашению текущих обязательств	Индикатор финансовой устойчивости компании
Коэффициент доходности инвестиций	Определяет эффективность инвестиций и их возвратность	Оценка успешности использования инвестиций

Таким образом, коэффициенты играют важную роль в экономическом анализе и позволяют получить информацию о различных аспектах экономической деятельности.