Что такое компоненты в математике 3 класс примеры

В статье рассматривается понятие компоненты в математике для учащихся 3 класса. Приводятся примеры задач и упражнений, которые помогут школьникам лучше понять и применять это понятие.

В математике компоненты — это числа или объекты, которые составляют другие числа или объекты. В третьем классе дети начинают изучать компоненты числа, чтобы лучше понимать его структуру и связь между его частями.

Примером компонентов числа может служить разложение числа на сумму двух или более чисел. Например, число 45 можно представить как сумму 40 и 5. В этом случае 40 и 5 являются компонентами числа 45.

Одним из способов представления компонентов числа является использование числовой линии. На числовой линии каждая компонента числа представлена своим отрезком. Например, для числа 45, отрезок от 0 до 40 представляет компоненту 40, а отрезок от 40 до 45 представляет компоненту 5.

Изучение компонентов числа помогает детям развивать навыки сложения и вычитания, а также понимание структуры числа. Это важный этап в их математическом образовании, который будет использоваться в дальнейшем изучении более сложных математических концепций.

Определение компонентов

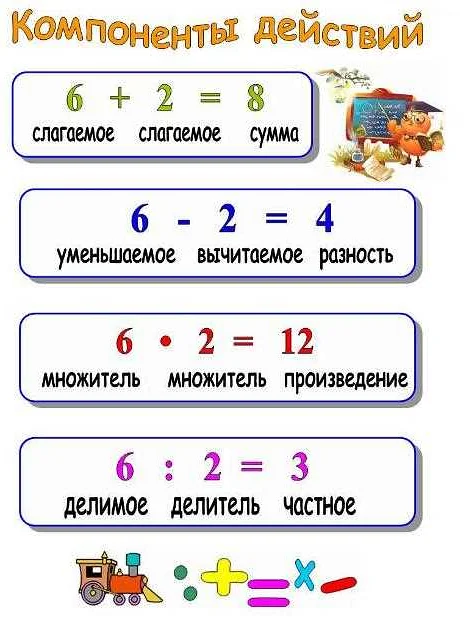
Целые компоненты представляют собой отдельные цифры, которые образуют число. Например, в числе 753, каждая цифра — это целый компонент.

Десятичные компоненты — это отдельные цифры после запятой, которые образуют десятичную часть числа. Например, в числе 3,14 цифры 1 и 4 являются десятичными компонентами.

Понимание компонентов помогает ученикам анализировать и понимать структуру чисел, а также выполнять операции с числами более эффективно.

Видео по теме:

Примеры компонентов

Пример 1:

Число 52 можно разложить на компоненты 50 и 2. Сложив эти компоненты, получим исходное число 52.

Пример 2:

Число 37 можно разложить на компоненты 30 и 7. Сложив эти компоненты, получим исходное число 37.

Пример 3:

Число 89 можно разложить на компоненты 80 и 9. Сложив эти компоненты, получим исходное число 89.

Таким образом, компоненты помогают разбить число на составные части и понять, как их сложить, чтобы получить исходное число.

Сложение компонентов

Компоненты числа — это его составные части, разделенные на разряды. К примеру, в числе 357 есть компоненты 300, 50 и 7. Чтобы выполнить сложение компонентов чисел, необходимо складывать соответствующие компоненты каждого числа по отдельности.

Например, если нам нужно сложить числа 345 и 207, мы складываем их компоненты по отдельности:

3 4 5

+ 2 0 7

———

5 4 12

В результате сложения компонентов чисел 345 и 207 мы получили число 5412.

Когда мы складываем компоненты, мы начинаем с самого правого разряда и двигаемся влево. Если сумма компонентов больше или равна 10, мы записываем только последнюю цифру суммы, а единицу переносим в следующий разряд. Если в одном из чисел разрядов не хватает, то его компонент считается равным нулю.

Например, если мы складываем числа 789 и 56, мы складываем их компоненты по отдельности:

7 8 9

+ 0 5 6

———

7 13 5

Так как сумма компонентов 9 и 6 больше 10, мы записываем только последнюю цифру 13 — 3, а единицу переносим в следующий разряд. В результате сложения компонентов чисел 789 и 56 мы получим число 7135.

Сложение компонентов является основой для выполнения сложения чисел в столбик и в десятичной системе счисления в целом. Понимание сложения компонентов поможет вам лучше понять основы математики и выполнять сложение чисел более эффективно.

Вопрос-ответ:

Что такое компоненты в математике?

Компоненты в математике — это отдельные составляющие числа или выражения, которые могут быть сложены или вычтены друг из друга.

Какие есть примеры компонентов в математике для 3 класса?

Примерами компонентов в математике для 3 класса могут быть числа (например, 5 и 3), арифметические выражения (например, 2 + 4 и 7 — 2), а также предметы или объекты, которые можно считать (например, 3 яблока и 2 груши).

Чем отличаются компоненты от результатов в математике?

Компоненты в математике — это отдельные числа или выражения, которые используются для выполнения операций (сложения, вычитания и т. д.), в то время как результаты — это конечные значения, получаемые после выполнения этих операций.

Какие математические операции можно выполнять с компонентами?

С компонентами можно выполнять различные математические операции, такие как сложение, вычитание, умножение и деление. Например, два числа (компонента) можно сложить, чтобы получить их сумму.

Зачем нужно знать о компонентах в математике?

Знание о компонентах в математике позволяет нам лучше понимать и выполнять различные математические операции. Знание компонентов позволяет нам разбивать сложные задачи на более простые части и решать их по отдельности.

Вычитание компонентов

Для выполнения вычитания компонентов необходимо следовать определенной последовательности действий:

1. Записать вычитаемое число или выражение под вычитателем.
2. Записать вычитатель над вычитаемым числом или выражением.
3. Выполнить вычитание по правилам:
   • Если вычитатель и вычитаемое являются числами, то вычитание производится в обычном порядке.
   • Если вычитатель и вычитаемое являются выражениями, то необходимо выполнить вычитание в каждом слагаемом отдельно.

Например, при выполнении операции 8 — 3 мы записываем 8 под вычитателем и 3 над вычитаемым числом. Затем вычитание производится в обычном порядке: 8 — 3 = 5.

Вычитание компонентов широко используется в математике для решения различных задач и примеров. Она помогает нам находить разницу между числами или выражениями и устанавливать отношения между ними.

Умножение компонентов

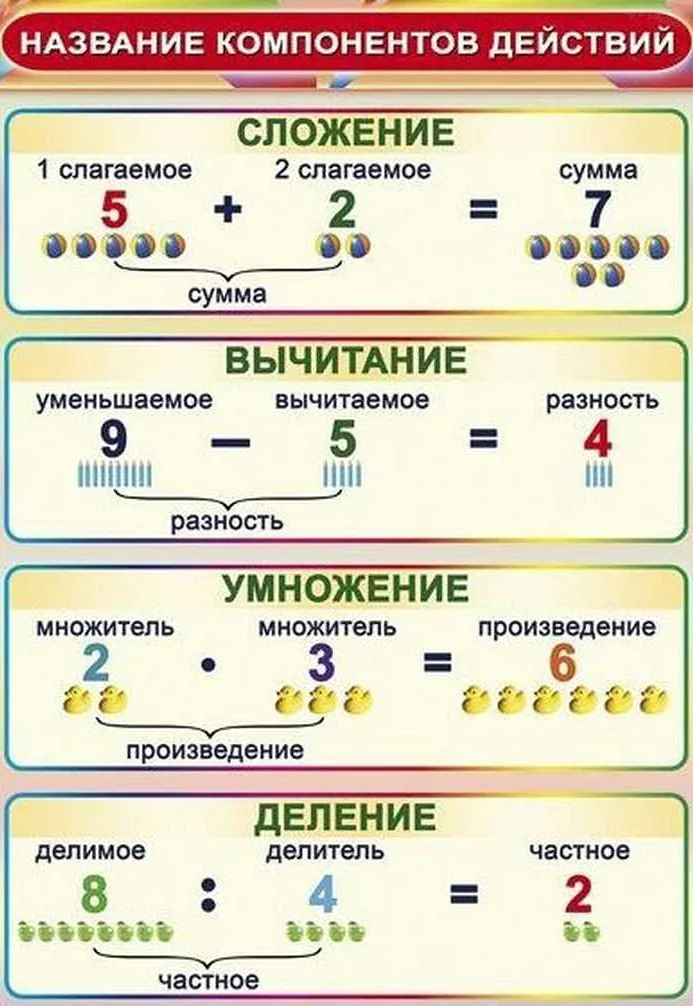
Для умножения компонентов необходимо умножить соответствующие компоненты каждого числа и сложить полученные произведения. Например, если у нас есть два числа: 23 и 45, то их компоненты будут 2 и 3, 4 и 5 соответственно. Умножив соответствующие компоненты, получим произведения: 2 * 4 = 8 и 3 * 5 = 15. Затем необходимо сложить полученные произведения: 8 + 15 = 23. Таким образом, произведение компонентов чисел 23 и 45 равно 23.

Метод умножения компонентов основан на свойствах умножения, таких как коммутативность и ассоциативность. Этот метод позволяет детям легко выполнять умножение и понимать его смысл.

Примеры заданий на умножение компонентов могут выглядеть следующим образом:

Множитель 1Множитель 2Произведение компонентовПроизведение

12	34	1 * 3 = 3 2 * 4 = 8	38
15	27	1 * 2 = 2 5 * 7 = 35	237

Выводя задания на умножение компонентов в таком формате, учителя помогают детям лучше понять процесс умножения и развивают их навыки в области математики.

Деление компонентов

Когда мы говорим о делении компонентов, мы имеем в виду разделение числа на равные части. При делении компонентов мы делим число на несколько одинаковых групп или компонентов.

Для примера, рассмотрим число 12. Мы можем разделить его на 4 компонента. В этом случае каждый компонент будет равен 12 ÷ 4 = 3. Таким образом, мы получаем 4 компонента, каждый из которых равен 3.

Деление компонентов может быть полезным при решении задач, связанных с распределением предметов или ресурсов. Например, если у нас есть 12 яблок и мы хотим разделить их между 4 детьми, мы можем использовать деление компонентов, чтобы найти сколько яблок получит каждый ребенок.

Деление компонентов также помогает нам понять, какие доли составляют каждый компонент от исходного числа. В примере с 12 яблоками и 4 детьми каждый ребенок получит 1/4 или 25% от общего количества яблок.

Таким образом, деление компонентов позволяет нам разделить число на равные части и определить долю каждой части от исходного числа. Это важная концепция в математике, которая используется для решения различных задач и понимания отношений между числами.

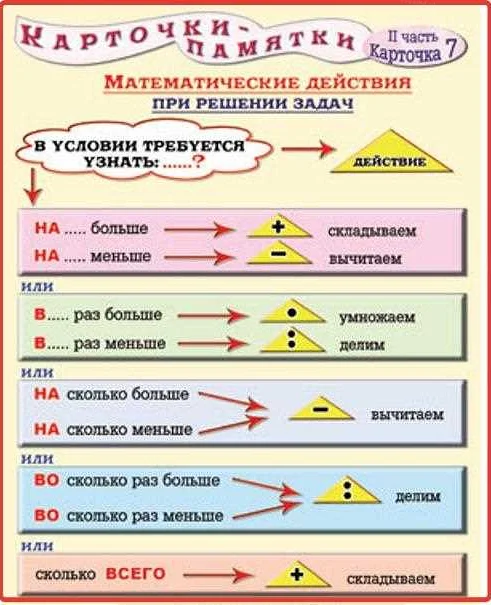
Закрепление материала по компонентам

После изучения компонентов в математике 3 класса, необходимо закрепить полученные знания. Для этого можно использовать различные упражнения, задачи и игры.

Одним из способов закрепления материала является решение задач на определение компонентов числа. Например, учитель может задать задачу: «Разложите число 24 на компоненты». Ученик должен будет найти все способы разложения числа 24 на два компонента (например, 12+12, 6+18 и т.д.). Это позволит ученику применить полученные знания на практике и закрепить их.

Также можно использовать игры для закрепления материала. Например, игра «Собери число» — учитель называет число, а ученик должен быстро найти его компоненты и назвать их. Игра «Кто быстрее?» — учитель задает вопросы с разложением числа на компоненты, а ученики соревнуются, кто первый назовет правильный ответ. Эти игры помогут ученикам быстро и точно находить компоненты числа и закрепить полученные знания.

Также можно использовать упражнения на составление чисел из компонентов. Например, учитель может дать ученикам таблицу с пустыми ячейками, в которых нужно записать компоненты числа. Ученики должны будут найти компоненты чисел и записать их в таблицу. Это поможет ученикам отработать навык составления чисел из компонентов и закрепить полученные знания.

Таким образом, закрепление материала по компонентам в математике 3 класса можно осуществлять с помощью задач, игр и упражнений. Это поможет ученикам закрепить полученные знания и научиться применять их на практике.