Кто придумал тождество в математике

Узнайте, кто придумал и формализовал понятие тождества в математике. История и развитие этого концепта в науке.

Тождество — одна из фундаментальных концепций в математике, которая играет важную роль в решении уравнений и доказательствах теорем. Однако, кто и когда придумал это понятие? В этой статье мы рассмотрим историю тождества и открытия, которые легли в его основу.

Изначально идея тождества появилась в Древней Греции, в период между V и IV веками до н.э., когда математики начали изучать алгебру и решение уравнений. Считается, что одним из первых, кто начал работать с тождествами, был древнегреческий математик Диофант Александрийский.

Диофант предложил применять алгебраические тождества для нахождения решений уравнений и доказательства различных математических фактов. Он разработал методы, позволяющие упростить уравнения, заменяя сложные выражения на эквивалентные, но более простые.

В последующие века математики продолжали разрабатывать и улучшать идеи Диофанта, внося свой вклад в теорию тождеств. В XIX веке появилось понятие формальной логики, которое стало основой для развития алгебры и теории тождеств в математике.

На протяжении всей истории математики были сделаны множество открытий и доказательств, связанных с тождествами. Сегодня тождество играет важную роль во многих областях математики, таких как алгебра, геометрия, математическая логика и др. Изучение и понимание тождеств позволяет решать сложные задачи и открывать новые закономерности в мире чисел и формул.

Как возникло тождество в математике?

Первые упоминания о тождестве встречаются в математических текстах Евклида, который жил в 3-ем веке до н.э. Его работы по элементарной геометрии содержали аксиоматическую систему, в рамках которой были доказаны множество тождественных отношений.

Однако, тождество в математике как области знания начало развиваться в 17-ом веке, благодаря работам ряда математиков, таких как Рене Декарт, Исаак Ньютон, Готфрид Лейбниц. Они разработали алгебру, которая стала основой для формализации и изучения тождественных отношений.

Алгебра предоставила математикам новый инструмент для работы с выражениями и уравнениями. Таким образом, они смогли систематизировать и классифицировать тождественные отношения, а также исследовать их свойства и применения в различных областях математики.

Кроме того, развитие алгебры способствовало разработке символьных методов решения математических задач. Это позволило упростить и ускорить процесс решения уравнений и систем уравнений, а также обобщить методы анализа и синтеза математических объектов.

С течением времени тождество получило широкое применение в различных областях математики, таких как алгебра, аналитическая геометрия, математическая логика и др. Оно стало неотъемлемой частью современной математической теории и является основой многих ее разделов.

Таким образом, тождество в математике возникло благодаря развитию алгебры и символьных методов, которые позволили исследовать и систематизировать равенства и уравнения, а также использовать их для решения различных математических задач.

Исторические корни тождества в математике

Одним из первых известных примеров использования тождества является принцип тождества Брахмагупты, который был сформулирован в древней Индии в 7 веке нашей эры. Этот принцип гласит, что произведение двух сумм квадратов равно сумме квадратов суммы и разности этих двух сумм.

Также в Индии были разработаны различные тождества, связанные с тригонометрией. Например, арксинусы и арккосинусы были выражены с помощью рядов, которые были представлены в виде бесконечных сумм. Это позволило получить точные значения для некоторых тригонометрических функций.

В Европе тождество начали изучать в средние века, особенно после появления алгебры. Одним из важнейших результатов было открытие тождества Виета в 16 веке. Он показал, что можно выразить корни многочлена через его коэффициенты.

С развитием математики в 19 и 20 веках было открыто множество новых тождеств и принципов. Например, в рамках абстрактной алгебры были разработаны теория групп и кольца, которые основаны на наборе тождеств. Также в математической логике были разработаны теории формальных систем, где тождество играет важную роль.

Сегодня тождество в математике является одной из основных концепций. Оно применяется во многих областях математики, физики, информатики и других наук. История и развитие тождества отражают богатство и многообразие математического знания.

Открытия и развитие тождества в математике

История тождества в математике насчитывает множество открытий и развития этого понятия. Одним из важных открытий стало развитие алгебры и введение алгебраических символов, что позволило записывать тождества компактно и систематизировано.

В древности тождество использовалось уже в математических работах, например, Евклид в своей «Начальной алгебре» приводил тождества для решения уравнений. Однако, формально это понятие было развито позже, в Средние века, благодаря работам арабских математиков. Они ввели символизацию алгебраических операций и дали определение тождества.

В новое время тождество получило еще большую развитость. В XVII веке Франсуа Виет предложил алгебраический язык и использовал буквы для обозначения неизвестных величин, что позволило записывать тождества в общем виде. Алгебраические символы и тождества стали одним из основных инструментов математического анализа.

Впоследствии тождество нашло применение во многих областях математики. Оно активно используется в алгебре, геометрии, математическом анализе и других разделах. Примерами тождеств могут служить формулы тригонометрии, алгебраические тождества, тождества в математической логике и т. д. Каждое новое открытие и развитие тождества вносит свой вклад в развитие математики в целом.

Тождество как основа математических доказательств

Тождество может быть выражено с помощью различных математических операций, таких как сложение, вычитание, умножение и деление. Например, тождество a + b = b + a утверждает, что сумма двух чисел не зависит от порядка слагаемых.

В математических доказательствах тождество может быть использовано для упрощения выражений, преобразования уравнений и установления равенств между различными математическими объектами. Оно позволяет переходить от известных фактов и свойств к новым выводам и следствиям.

Исторически, тождество было открыто и разработано различными математиками на протяжении многих веков. Они устанавливали и проверяли различные математические свойства и отношения, которые впоследствии были сформулированы в виде тождеств.

Сегодня тождество является основой математических доказательств и играет важную роль во многих областях математики, включая алгебру, анализ, геометрию и дискретную математику. Оно позволяет строить логические цепочки рассуждений и выводить новые математические результаты на основе уже установленных фактов.

Примеры применения тождества в математических задачах

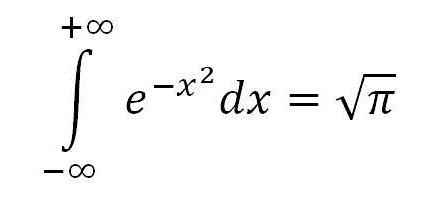
Пример 1: Решение уравнения. Пусть дано уравнение x + 3 = 7. Используя тождество x + a = b, где a и b — известные числа, мы можем найти значение переменной x. В данном случае, мы знаем, что a = 3 и b = 7, поэтому x + 3 = 7. Применяя тождество, мы можем вычесть 3 из обеих сторон уравнения и получить ответ: x = 4.

Пример 2: Упрощение выражений. Тождество a(b + c) = ab + ac позволяет нам упростить выражения, содержащие скобки. Например, рассмотрим выражение 2(3 + 4). Применяя тождество, мы можем умножить число 2 на каждый из элементов в скобках и получить: 2(3 + 4) = 2·3 + 2·4 = 6 + 8 = 14.

Пример 3: Доказательство равенств. Тождество может быть использовано для доказательства равенств. Например, чтобы доказать, что (a + b)² = a² + 2ab + b², мы можем применить тождество (a + b)² = a² + 2ab + b² и убедиться, что обе части равны. Это доказательство показывает, что выражения на обеих сторонах равны друг другу.

Таким образом, тождество играет важную роль в математике и помогает нам решать уравнения, упрощать выражения и доказывать равенства. Оно является одним из основных инструментов, используемых в математических задачах.

Тождество в алгебре и анализе

В алгебре тождество обычно представляется в виде равенства двух алгебраических выражений, которое верно для любых значений переменных. Например, тождество (a+b)^2 = a^2 + 2ab + b^2 справедливо для любых значений переменных a и b.

В анализе тождество может быть представлено в виде равенства двух функций, которое верно для всех значений аргументов. Например, тождество sin^2(x) + cos^2(x) = 1 справедливо для любого значения аргумента x.

Тождества в алгебре и анализе используются для упрощения выражений, доказательства теорем и нахождения значений функций. Они являются основой многих математических операций и теорий.

АлгебраАнализ

Тождество (a+b)^2 = a^2 + 2ab + b^2	Тождество sin^2(x) + cos^2(x) = 1
Тождество a^2 — b^2 = (a+b)(a-b)	Тождество (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
Тождество (a+b)^n = a^n + C(n,1)a^(n-1)b + C(n,2)a^(n-2)b^2 + … + C(n,n-1)ab^(n-1) + b^n	Тождество d/dx(e^x) = e^x

Тождества в алгебре и анализе являются основой для дальнейшего изучения математики и применяются в различных областях науки и техники.

Связь тождества с другими математическими понятиями

Во-первых, тождество тесно связано с понятием равенства. Оно используется для выражения того, что два математических выражения равны друг другу. Тождество позволяет утверждать, что две стороны уравнения являются эквивалентными и имеют одно и то же значение.

Во-вторых, тождество является основой для доказательств в математике. Оно позволяет преобразовывать и упрощать выражения, используя различные математические операции и свойства. Доказательства теорем и утверждений основываются на использовании тождественных преобразований, которые позволяют получить новые равенства и утверждения.

Также тождество имеет связь с понятием функций. В математическом анализе тождество используется для определения границы функции и ее свойств в пределах этой границы. Тождество позволяет анализировать функции и строить их модели, используя различные математические методы.

Тождество также связано с понятием идентичности. Оно позволяет утверждать, что два математических объекта являются одинаковыми или эквивалентными. Идентичность может быть выражена с помощью тождества и используется для доказательства математических тождеств и равенств.

В заключение, тождество играет важную роль в математике и имеет связь с другими важными понятиями. Оно используется для выражения равенства, преобразования и упрощения выражений, а также для анализа функций и доказательства идентичности математических объектов.

Видео по теме:

Вопрос-ответ:

Какое тождество в математике считается самым известным?

Самым известным тождеством в математике считается теорема Пифагора, которая устанавливает соотношение между длинами сторон прямоугольного треугольника.

Кто придумал тождество в математике?

История тождеств в математике насчитывает множество открытий, и авторами этих открытий были разные математики. Например, теорема Пифагора была открыта Пифагором самим. Евклид также внес большой вклад в развитие тождеств в математике. Однако, некоторые тождества не имеют конкретных авторов и разрабатывались коллективно или постепенно развивались с течением времени.

Какие еще известные тождества существуют в математике?

В математике существует множество известных тождеств. Некоторые из них включают формулы для вычисления площадей и объемов геометрических фигур, например, формулы для вычисления площади круга или объема цилиндра. Еще одно известное тождество — формула Эйлера для многогранников, которая связывает количество вершин, ребер и граней в многограннике.

Каким образом тождества используются в математике?

Тождества в математике используются для доказательства других утверждений или для решения математических задач. Они позволяют упростить сложные выражения и перейти к более простым формулам или равенствам. Также тождества могут использоваться для установления связей между разными областями математики и для построения новых математических объектов и теорий.

Какие важные открытия были сделаны в области тождеств в математике?

В области тождеств в математике были сделаны множество важных открытий. Например, открытие формулы для вычисления площади круга или объема цилиндра позволило развить геометрию и применить ее в различных практических задачах. Также были сделаны открытия в области алгебры, например, формулы для решения квадратных уравнений или теорема Ферма, которая была доказана после многовековых попыток.

Кто придумал тождество в математике?

Авторство открытия тождеств в математике принадлежит нескольким ученым. Одним из первых, кто работал над этой темой, был древнегреческий математик Евклид. Он в своих работах активно использовал тождества для доказательства различных утверждений. В дальнейшем, в разные периоды истории, другие математики также внесли свой вклад в развитие теории тождеств.

Влияние тождества на развитие математики

Впервые понятие тождества было формализовано и систематизировано в древнегреческой математике. Открытие тождества позволило математикам проводить логические исследования, доказывать теоремы и решать сложные задачи.

В дальнейшем, с развитием алгебры и математической логики, понятие тождества стало одной из фундаментальных концепций. Оно нашло широкое применение в различных областях математики, включая анализ, геометрию, теорию чисел и другие.

Тождество позволяет устанавливать равенства между различными выражениями и объектами, что делает возможным решение сложных математических задач. Оно помогает строить логические цепочки рассуждений, выводить новые результаты и открывать новые области исследования.

С развитием компьютерных технологий и появлением компьютерных программ для символьных вычислений, понятие тождества получило новые возможности. С его помощью можно проводить сложные математические вычисления и доказательства, автоматизировать процессы исследования и обнаружения новых свойств и закономерностей.

Таким образом, тождество играет важную роль в развитии математики, помогает математикам исследовать свойства и взаимосвязи различных математических объектов, решать сложные задачи и открывать новые области исследования.

Современные исследования и применения тождества

Одной из областей, где тождество находит свое применение, является алгебра. Здесь тождества используются для решения уравнений и систем уравнений, а также для анализа структуры алгебраических объектов. Они позволяют устанавливать связь между различными алгебраическими операциями и свойствами объектов.

Тождества также активно используются в математической логике и теории доказательств. Они позволяют устанавливать эквивалентность между различными высказываниями и упрощать процесс доказательства. Также тождества применяются для формализации математических теорий и построения формальных систем.

В теории чисел тождества используются для изучения свойств чисел и отношений между ними. Они помогают устанавливать различные равенства и неравенства, а также анализировать структуру числовых последовательностей и рядов.

Тождества находят свое применение и в других областях математики, таких как теория вероятностей, комбинаторика, математическая физика и др. Они позволяют моделировать различные математические задачи и изучать их свойства с помощью формулирования и решения тождеств.

Современные исследования в области тождеств позволяют расширять наши знания о математике и применять ее во многих практических областях. Они способствуют развитию науки и технологий, а также находят свое применение в различных прикладных задачах.